九大基础排序算法总结
Posted yccy1230
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了九大基础排序算法总结相关的知识,希望对你有一定的参考价值。
九大基础排序算法小结
一直想做份总结,总是抽不出时间,趁着周末闲着直接用了一整天做一份,一些内容参考了网上的一些博主的总结,还有网络上的一些图片。
好了,接下来就看看内容吧!
排序算法:
| 排序方法 | 时间复杂度 | 空间复杂度 | 稳定性 | 选用情况 | ||
| 平均情况 | 最坏情况 | 最好情况 | ||||
| Insertion Sort | O(n^2) | O(n^2) | O(n) | O(1) | 稳定 | n较小时 |
| Selection Sort | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 | n较小时 |
| Bubble Sort | O(n^2) | O(n^2) | O(n) | O(1) | 稳定 | n较小时 |
| Shell Sort | O(nlog2n) | O(n^s) | O(nlog2n) | O(1) | 不稳定 | S是所选组数 |
| Quick Sort | O(nlog2n) | O(n^2) | O(nlog2n) | O(nlog2n) | 不稳定 | n较大时 |
| Merge Sort | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(1) | 稳定 | n较大时 |
| Heap Sort | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(1) | 不稳定 | n较大时 |
| Radix Sort | O((n+r)d) | O((n+r)d) | O((n+r)d) | O(n+r) | 稳定 | 位数少,数据量大 |
| Tree Sort | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(1) | (不允许出现重复数字) | 基本无序时 |
注:Radix Sort中n=数字个数; r=分配后链表的个数;d=数字或字符串的位数.
1.插入排序(Insertion Sort)
1)算法描述:
| · Step1:将待排序数组分为有序和无序两组(初始情况下有序组为第一个元素) · Step2:取出无序组第一个元素(First_unsorted)放入临时空间,将first_unsorted与有序组从最后一个元素开始进行比较,如果比有序组小,则将有序组中的该元素向后移一位,直到找到第一个比first_unsorted小的时候,将first_unsorted放入。至此,有序组++,无序组--。 · Step3:重复step2,直到无序组数量为0.
算法结束。 |
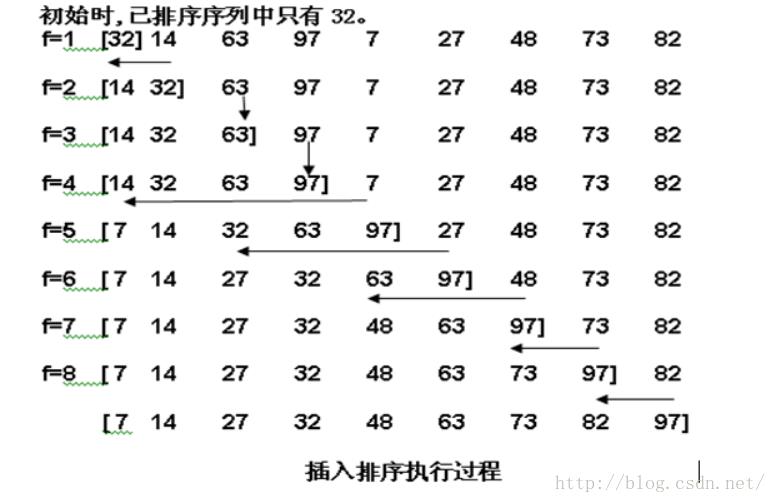
2)适用情况分析:
| · 稳定 · 数组,链表均可实现 · 空间复杂度O(1) · 时间复杂度O(n2) · 最差情况:反序,需要移动n*(n-1)/2个元素 · 最好情况:正序,不需要移动元素 · 数据量较小,较有序的情况下性能较好
|
3)参考代码:
顺序版本↓:
template<class List_entry>
void Sortable_List<List_entry>::insertion_sort()
{
List_entry current;
if (count == 0)return;
for (int first_unsorted = 1; first_unsorted < count; first_unsorted++) {
if (entry[first_unsorted] >= entry[first_unsorted - 1])continue;
current = entry[first_unsorted];
int position = first_unsorted;
do {
entry[position] = entry[position - 1];
position--;
} while (position > 0 && entry[position - 1] > current);
entry[position] = current;
}
}
链式版本↓:
template<class List_entry>
void Sortable_list<List_entry>::insertion_sort()
{
Node<List_entry> *first_unsorted, *last_sorted, *current, *previous;
if (head == NULL)return;
last_sorted = head;
while (last_sorted->next){
first_unsorted = last_sorted->next;
if (first_unsorted->entry < head->entry) {
last_sorted->next = first_unsorted->next;
first_unsorted->next = head;
head = first_unsorted;
}
else {
previous = head;
current = previous->next;
while (current->entry < first_unsorted->entry) {
previous = current;
current = current->next;
}
if (current == first_unsorted)last_sorted = first_unsorted;
else {
last_sorted->next = first_unsorted->next;
first_unsorted->next = current;
previous->next = first_unsorted;
}
}
}
}
2.选择排序(selection Sort)
1)算法描述:
| · Step1:将待排序数组分为有序和无序两组(初始情况下有序组为空) · Step2:从左向右扫描无序组,找出最小的元素,将其放置在无序组的第一个位置。至此有序组++,无序组--; · Step3:重复Step2,直至无序组只剩下一个元素。
算法结束。 |
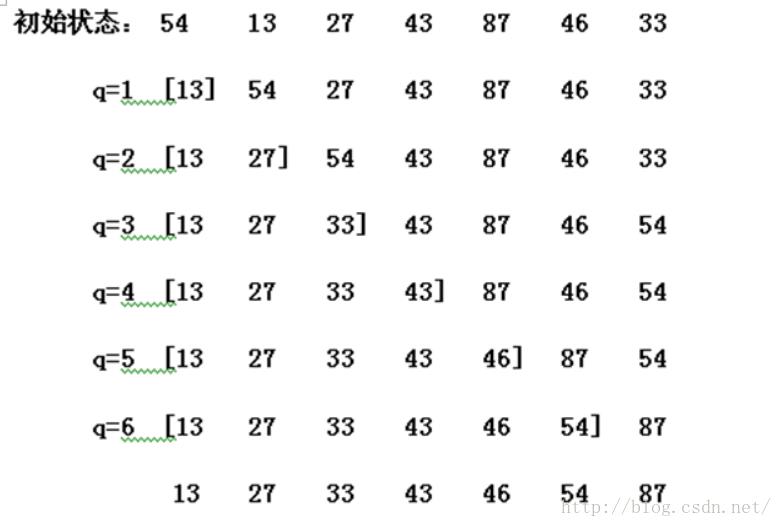
2)适用情况分析:
| · 不稳定 · 数组,链表均可实现 · 空间复杂度:O(1) · 时间复杂度:O(n2) · 最坏情况:O(n2) 第一个元素为最大元素,其余元素正序,需要交换n-1个元素(如:4 3 2 1) · 最好情况:O(n2) 正序,不需要交换元素 · 选择排序的最坏情况和最好情况下的实际没有太大区别。即选择排序对于原始记录的顺序不敏感。
|
3)参考代码:
template<class List_entry>
void Sortable_List<List_entry>::selection_sort()
{
for (int i = 0; i < count - 1; i++) {
int min = min_key(i, count - 1);
swap(min, i);
}
}
template<class List_entry>
int Sortable_List<List_entry>::min_key(int low, int high)
{
int min = low;
for (int i = low + 1; i <= high; i++) {
if (entry[min] > entry[i])min = i;
}
return min;
}
template<class List_entry>
void Sortable_List<List_entry>::swap(int low, int high)
{
List_entry tmp = entry[low];
entry[low] = entry[high];
entry[high] = tmp;
}
3. 冒泡排序(Bubble Sort)
1)算法描述:
| · Step1:比较相邻的元素。如果第一个比第二个大,就交换他们两个 · Step2:对每一对元素均进行此操作,经过一轮后最大的元素应位于最后一位 · Step3:从第一个元素重复进行前两步,每一轮最后一个元素都不参与比较,进行n轮 算法结束。 |
2)适用情况分析:
| 稳定 · 大部分采取顺序,链式也可实现 · 空间复杂度O(1) · 时间复杂度O(n2) · 数据顺序对算法影响不大 |
3)参考代码:
template<class List_entry>
void Sortable_List<List_entry>::bubble_sort()
{
for(int i=0;i<count;i++)
for (int j = 0 ; j < count-i-1; j++)
if (entry[j] > entry[j+1]) {
List_entry tmp = entry[j];
entry[j] = entry[j + 1];
entry[j + 1] = tmp;
}
}
4.希尔排序(Shell Sort)---插入排序的优化
1)算法描述:
| · Step1:先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序 · Step2:依次缩减增量再进行排序 · Step3:待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序
算法结束
因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序相较于前几种方法有较大的提升 |

2)适用情况分析:
| · 不稳定 · 采取顺序实现,对下标敏感 · 空间复杂度O(1) · 时间复杂度O(nlogn) · 步长的选择是希尔排序的重要部分。只要最终步长为1任何步长序列都可以工作。 · Donald Shell 最初建议步长选择为N/2并且对步长取半直到步长达到1 · 已知的最好步长序列是由Sedgewick提出的(1, 5, 19, 41, 109,...) |
3)参考代码:
template<class List_entry>
void Sortable_List<List_entry>::shell_sort()
{
int increment = count;
do {
increment = increment / 3 + 1;
for (int start = 0; start < increment; start++)
sort_interval(start, increment);
} while (increment > 1);
}
template<class List_entry>
void Sortable_List<List_entry>::sort_interval(int start, int increment)
{
List_entry current;
int position;
for (int first_unsorted = start + increment; first_unsorted < count;
first_unsorted += increment) {
if (entry[first_unsorted] < entry[first_unsorted - increment]) {
position = first_unsorted;
current = entry[position];
do {
entry[position] = entry[position - increment];
position -= increment;
} while (position > start&&entry[position - increment] > current);
entry[position] = current;
}
}
}
在网络上看到了简化版本的shell sort,也可作参考:
void shellsort3(int a[], int n)
{
int i, j, gap;
for (gap = n / 2; gap > 0; gap /= 2)
for (i = gap; i < n; i++)
for (j = i - gap; j >= 0 && a[j] > a[j + gap]; j -= gap)
swap(a[j], a[j + gap]);
}
5.快速排序(Quick Sort)
1)算法描述:
| · Step1:在待排序列中选取一个轴点(pivot),通常选取中间点 · Step2:将轴点与其他元素进行比较,将比轴点小的元素放在轴点之前,比轴点大的元素放在轴点之后。至此,pivot已被排好序 · Step3:对0-(pivot-1)和(pivot+1)-n分别递归进行上述两步。 算法结束。 |

2)适用情况分析:
| · 不稳定。 · 顺序实现 · 空间复杂度:O(1) · 时间复杂度:O(nlog2n) · 最坏情况:O(n2)要排序数组基本有序,基准值每次取最大(最小)元素,退化为冒泡。 · 最好情况:O(nlog2n) 基准值两边元素个数基本相同. |
3)参考代码:
template<class List_entry>
void Sortable_List<List_entry>::quick_sort()
{
do_quick_sort(0, count - 1);
}
template<class List_entry>
void Sortable_List<List_entry>::do_quick_sort(int low, int high)
{
int pivot_position;
if (low < high) {
pivot_position = partition(low, high);
do_quick_sort(low, pivot_position - 1);
do_quick_sort(pivot_position + 1, high);
}
}
template<class List_entry>
int Sortable_List<List_entry>::partition(int low, int high)
{
List_entry pivot;
swap(low, (low + high) / 2); //将pivot放置到第一位
pivot = entry[low];
int last_small = low;
for (int i = low + 1; i <= high; i++)
if (entry[i] < pivot) swap(last_small++, i); //比pivot小的元素前移
swap(low, last_small); //将pivot放回
return last_small;
}
6.归并排序(Merge Sort)
1)算法描述:
| Step1:把待排序的列表划分为分成近似相等的两部分 Step2:分别将两个子列表排序(递归进行) Step3:然后再合并成一个完整的列表 算法结束。 |
2)使用情况分析:
| · 稳定 · 链式实现 · 空间复杂度:O(n) · 时间复杂度:O(nlog2n) · 最坏情况:O(nlog2n) · 最好情况:O(nlog2n) |
3)参考代码:
template<class List_entry>
void Sortable_list<List_entry>::mergesort(Sortable_list<List_entry> & list)
{
Sortable_list secondlist;
if (list.size() > 1) {
mergedivide(list, secondlist);
mergesort(list);
mergesort(secondlist);
mergecombine(list, secondlist);
}
}
template<class List_entry>
void Sortable_list<List_entry>::mergecombine(Sortable_list<List_entry> & firstlist, const Sortable_list<List_entry> & secondlist)
{
Sortable_list tmp;
List_entry x, y;
int n = 0, m = 0, i = 0;
while (n < firstlist.size() && m < secondlist.size()) {
firstlist.retrieve(n, x);
secondlist.retrieve(m, y);
if (x <= y) {
tmp.insert(i++, x);
n++;
}
else {
tmp.insert(i++, y);
m++;
}
}
while (n < firstlist.size()) {
firstlist.retrieve(n++, x);
tmp.insert(i++, x);
}
while (m < secondlist.size()) {
secondlist.retrieve(m++, y);
tmp.insert(i++, y);
}
firstlist = tmp;
}
template<class List_entry>
void Sortable_list<List_entry>::mergedivide(Sortable_list<List_entry>& firstlist, Sortable_list<List_entry>& secondlist)
{
int mid = (firstlist.size() - 1) / 2 + 1;
List_entry x;
for (int i = 0; firstlist.retrieve(mid, x)==success; i++) {
secondlist.insert(i, x);
firstlist.remove(mid, x);
}
}
7.堆排序(Heap Sort)
1)算法描述:
| 堆的定义:堆是一棵完全二叉树或者是近似完全二叉树。根结点(亦称为堆顶)的关键字是堆里所有结点关键字中最小者的堆称为小根堆,又称最小堆。根结点(亦称为堆顶)的关键字是堆里所有结点关键字中最大者,称为大根堆,又称最大堆。
· Step1:建堆,序列分成无序和有序两组(初始有序为0) · Step2:取出堆顶最大的元素,与待排序列的最后一个元素作交换,至此,无序组--,有序组++,并对无序组进行堆调整 · Step3:重复上述步骤,直至无序组仅剩一个元素 算法结束。 |
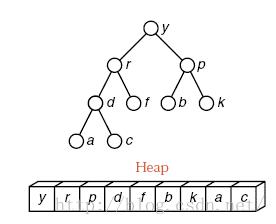
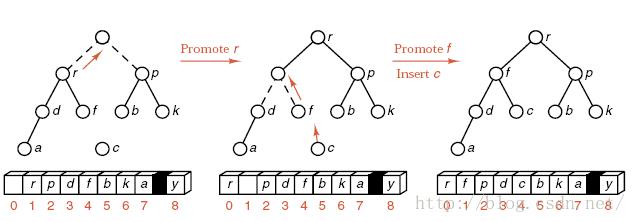
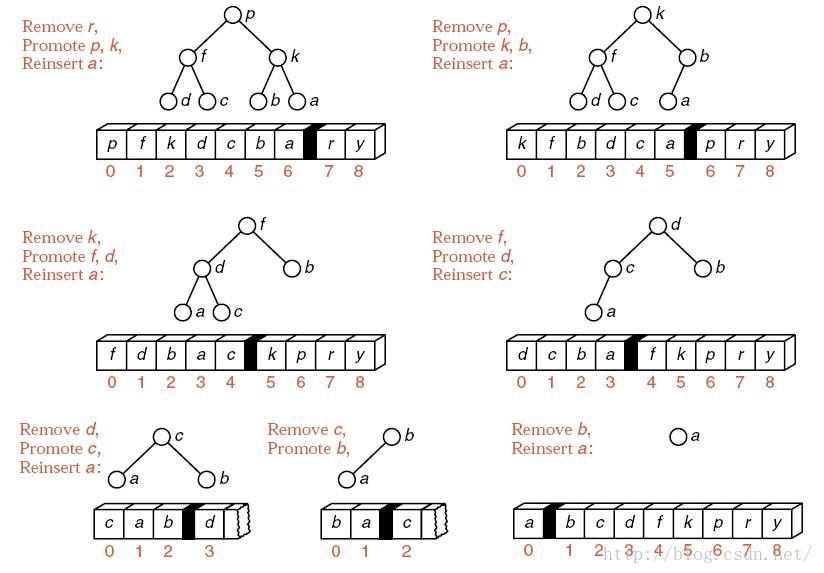
2)使用情况分析:
| 不稳定 顺序结构实现 时间复杂度:o(nlogn) 空间复杂度:o(1) 由于建初始堆所需的比较次数较多,不建议在数据量小的情况下使用 |
3)参考代码:
template<class List_entry>
void Sortable_List<List_entry>::heap_sort()
{
build_heap(); //建堆
for (int last_unsorted = count - 1; last_unsorted > 0; last_unsorted--) {
List_entry current = entry[last_unsorted];
entry[last_unsorted] = entry[0];
insert_heap(current, 0, last_unsorted - 1); //将最后一个元素插入堆中,获取下一个最值
}
}
template<class List_entry>
void Sortable_List<List_entry>::insert_heap(const List_entry & current, int low, int high)
{
int large = 2 * low + 1;
while (large <= high) {
if (large < high&&entry[large] < entry[large + 1])
large++; //将下标large调整为最大孩节点
if (entry[large] < current)break;
else { //promote entry[large]
entry[low] = entry[large];
low = large;
large = 2 * low + 1;
}
}
entry[low] = current;
}
template<class List_entry>
void Sortable_List<List_entry>::build_heap()
{
for (int low = count / 2 - 1; low >= 0; low--) {
List_entry current = entry[low];
insert_heap(current, low , count - 1);
}
}
8.基数排序(Radix Sort)
1)算法描述:
| LSD: Step1:将待排序的元素按照最后一位进行分桶操作(桶按照最后一位排序从大到小) Step2:按顺序将各个桶中的数据连接起来,形成新的序列 Step3:依次对新序列的倒数第二位至第一位进行上述两步操作 算法结束
MSD: Step1:将待排序的元素按照最高位进行分桶操作 Step2:对每个桶的按照第二位进行再次分桶(递归进行) Step3:进行至最后一位分桶操作完成后,对每个桶进行合并操作,得到有序序列 算法结束 |
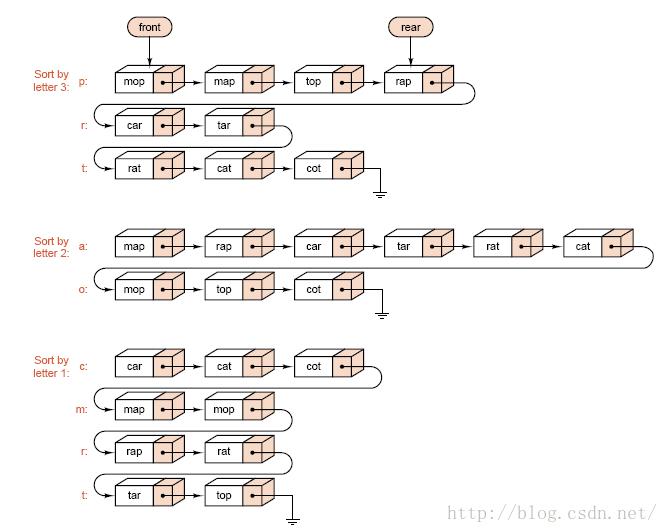
2)使用情况分析:
| · 稳定 · 链式实现 · 时间复杂度:假设在基数排序中,r为基数,d为位数。则基数排序的时间复杂度为O(d(n+r)) · 空间复杂度:在基数排序过程中,对于任何位数上的基数进行“装桶”操作时,都需要n+r个临时空间 · 数据量大时有明显优势,通常使用LSD法 |
3)参考代码:
MSD:
int alphabetic_order(char c)
{
if (c == ' ' || c == '\\0') return 0;
if (c >= 'a'&&c <= 'z')return (c - 'a' + 1);
if (c >= 'A'&&c <= 'Z')return (c - 'A' + 1);
return 27;
}
void Sortable_list::rethread(queue<Record> queues[])
{
Record x;
for (int i = 0; i < max_char; i++)
while (!queues[i].empty()) {
x = queues[i].front();
insert(size(), x);
queues[i].pop();
}
}
void Sortable_list::MSD_radix_sort()
{
Record data;
queue<Record> queues;
while(remove(0,data)==success){
queues.push(data);
}
sort(queues, key_size);
}
LSD:
void Sortable_list::LSD_radix_sort()
{
Record data;
queue<Record> queues[max_char];
for (int position = key_size - 1; position >= 0; position--) {
// Loop from the least to the most significant position.
while (remove(0, data) == success) {
int queue_number = alphabetic_order(data.key_letter(position));
queues[queue_number].push(data); // Queue operation.
}
rethread(queues); // Reassemble the list.
}
}
9.树排序(Tree Sort)
1)算法描述:
| 对于一棵二叉查找树,中序遍历的序列即为有序序列。 因此,二叉查找树的插入过程也可以看成是排序的过程。即 · Step1:将无序序列逐一插入二叉排序树。 · Step2:对二叉排序树进行中序遍历 算法结束 |
2)适用情况分析:
| · 不稳定 · 链式实现 · 时间复杂度:o(nlogn) · 空间复杂度:o(1) · Tree sort比较适合于无序的序列,对于基本有序的序列效率较低
|
3)参考代码:
template<class Record>
Error_code Binary_search_tree<Record>::c_insert(const Record & item)
{
Binary_node<Record> *&tmp=root;
if(!tmp)root = new Binary_node<Record>(item);
else {
while (tmp != NULL) {
if (tmp->data > item)tmp = tmp->left_child;
else if (tmp->data < item)tmp = tmp->right_child;
else return duplicate_error;
}
tmp = new Binary_node<Record>(item);
return success;
}
}
template<class Entry>
void Binary_tree<Entry>::recursive_inorder(Binary_node<Entry>* sub_root, void(*visit)(Entry &))
{
if (sub_root) {
recursive_inorder(sub_root->left_child,visit);
(*visit)(sub_root->data);
recursive_inorder(sub_root->right_child, visit);
}
}
template<class Entry>
void Binary_tree<Entry>::recursive_inorder(Binary_node<Entry>* sub_root, void(*visit)(Entry &))
{
if (sub_root) {
recursive_inorder(sub_root->left_child,visit);
(*visit)(sub_root->data);
recursive_inorder(sub_root->right_child, visit);
}
}
做的有些仓促,还望大家指正错误。
以上是关于九大基础排序算法总结的主要内容,如果未能解决你的问题,请参考以下文章