多变量微积分笔记12——平面向量场

Posted 2020-10-30 我是8位的

当研究物理系统中温度、压力、密度等在一定空间内的分布状态时，数学上只需用一个代数量来描绘，这些代数量（即标量函数）所定出的场就称为标量场。最常用的标量场有温度场，电势场，密度场，浓度场等等。

　　当研究物理系统中温度、压力、密度等在一定空间内的分布状态时，数学上只需用一个代数量来描绘，这些代数量（即标量函数）所定出的场就称为标量场。最常用的标量场有温度场，电势场，密度场，浓度场等等。

　　向量场 vector field（矢量场）是由一个向量对应另一个向量的函数。向量场广泛应用于物理学，尤其是电磁场。

　　建立坐标系(x,y,z)。空间中每一点(x₀,y₀,z₀)都可以用由原点指向该点的向量表示。因此，如果空间在所有点对应一个唯一的向量(a,b,c)，那么时空中存在向量场F: (x₀,y₀,z₀)→(a,b,c)

平面向量场

　　在二维平面上的每个点都对应一个向量，可以如下表示：

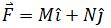
　　其中i和j是单位向量，M和N是关于x和y的函数，也就是平面向量场中的所有向量都取决于x和y。

　　场的概念其实很常见，比如风向场，每一点的风都可以用一个向量表示：

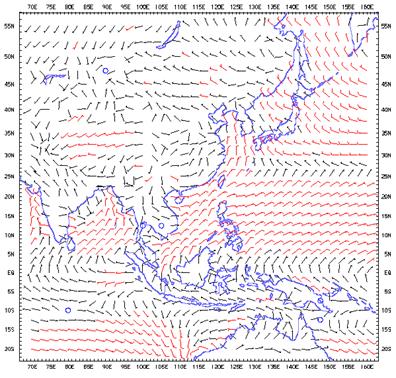
　　台风的风向场：

　　在物理学中常见的还有水流场和引力场。在流体中，每一点都有速度和力量；在地球上，所有物体都受到重力的约束，共同组成重力场；宇宙中，行星之间相互吸引或排斥，形成引力场。

向量场绘图

示例1：F = 2i + j

　　这个场向量有点特殊，它并不取决于x和y，也就是说所有点处的向量都相等，每个点处都存在向量<2, 1>：

 

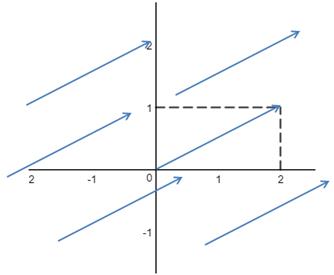
　　大概就是这样了，画出草图即可。向量是表示大小和方向的量，并未规定起点的位置。

示例2：F = xi

　　对于这个向量场来说，只存在i方向的分量，不存在j方向的分量，如果用四边形法做向量，这个四边形的高将压缩为0：

 

　　如上图所以，这将得到一个水平的向量。所以这个向量场是水平的，它不存在j方向上的分量，并且长度取决于x，如果x = 0，就是零向量。

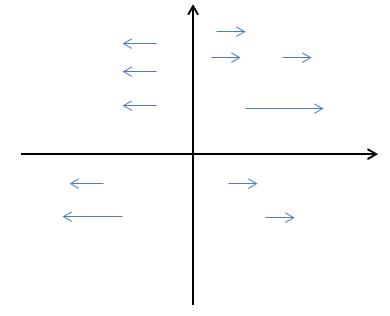
示例3：F = xi + yj

　　这里x和y可以是任意数据，而且未限定二者的关系。当y = 0时就是示例2中草图；如果x = y = 1，会有如下向量场：

　　对于F = xi + yj来说，这太过于杂乱无章，所以对于任意x和y，仅画出从原点出发的向量，这样F = xi + yj这个向量场将是从原点呈放射状，大小等于向量终点与原点的距离：

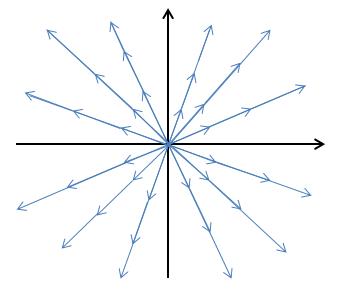
　　这可以看作是从一个点喷出的气流。

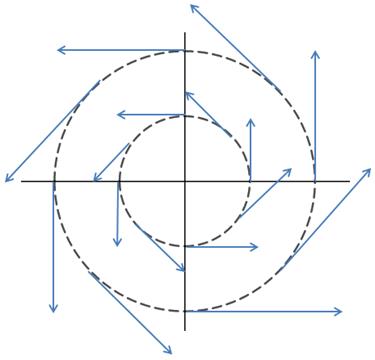
示例4：F = -yi + xj

　　当x = 1,y = 2时，向量<1,2>和 <-2,1>是垂直的：

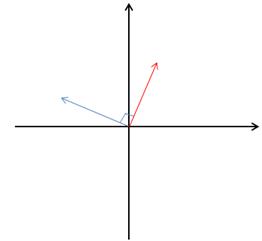
　　对于其它点也一样，<-y,x>⊥<x,y>。这可以用点积计算，两个向量的点积为0，则两个向量垂直：

 

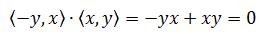
　　把上图的向量移动一下：

 

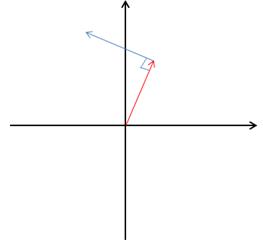
　　F = -yi + xj实际上是一个逆时针匀速转动的向量场，每个向量都与圆相切：

 

---

 　　作者：我是8位的

 　　出处：http://www.cnblogs.com/bigmonkey

 　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

 　　扫描二维码关注公众号“我是8位的”