深入浅出：快速排序

Posted 2020-10-30 panzi

　　前言

　　排序算法有很多，快速排序是能够突破时间复杂度 O(n2)的算法之一。下文中将由浅入深的介绍快速排序的原理。

分而治之

　　分而治之是一种解决问题的思路，有那么一点“大事化小，小事化了”的感觉。举个例子：求出数组 [1,2,3,5,6,9,8]所有项的和。那么我们首先想到的是遍历数组，每个元素相加即可。

for(int i=0;i<arr.length;i++){
     sum = sum + arr[i];  
}

　　那么采用分而治之的策略怎么解决呢？

　　首先我们大家都知道，如果数组只有一个元素 [1] 那么它的各项元素相加的结果就是 1。所以再看原数组： [1,2,3,5,6,9,8]。那么我们可以把它拆分成  [1] + [2,3,5,6,9,8] .同理，继续往下拆，[2,3,5,6,9,8] = [2] + [3,5,6,9,8] 。那么如此我们就可以用递归的方式实现，递归条件：数组的内元素的个数大于1个。终止递归（基线）条件，数组元素为1个。根据此思路，写出递归伪代码：

int sum(int[] arr){

  if(arr.length==0){
     return 0;  
  }

  if(arr.length  ==1){
      return arr[0];  
  }
  //返回数组第一个元素和后续元素的和, head(arr)代表第一个元素，相当于 arr[0] 然后将 tail(arr)进行sum运算
  return head(arr) + sum(tail(arr));
}

　　

　　运算过程就被分解为：1+[2,3,5,6,9,8]=1+2+[3,5,6,9,8]=1+2+3+[5,6,9,8]=.......=1+2+3+5+6+9+[8] = 34

　　当然，递归是一种解题思路，效率是没有直接for循环效率高的。并且占用方法调用栈也比较深。

　　下面再看一个例子：求出一个数组中最大的元素。 例如：max([1,2,3,5,6,9,8]) = 9,同理，使用分而治之的方法，用数组第一个元素 和 剩下元素组成的数组的最大值比较。伪代码如下：

int maxResult = head[arr] > max(tail(arr)) ?  head[arr]:max(tail(arr));

快速排序

　　终于进入正题 了。之所以先让大家理解分而治之的思路，就是因为快速排序与上述的思路是一致的。我们先看一下快速排序的思路。

　　现在有一个无序数组： [6,5,1,4,2,8,9] .思路就是选择一个基数，将数组中比基数小的放在基数的左边，比基数大的放在基数的右边。我们取基数 len /  2  取得元素 4。根据上述规则，那么数组排序过程演变如下：

　　

 

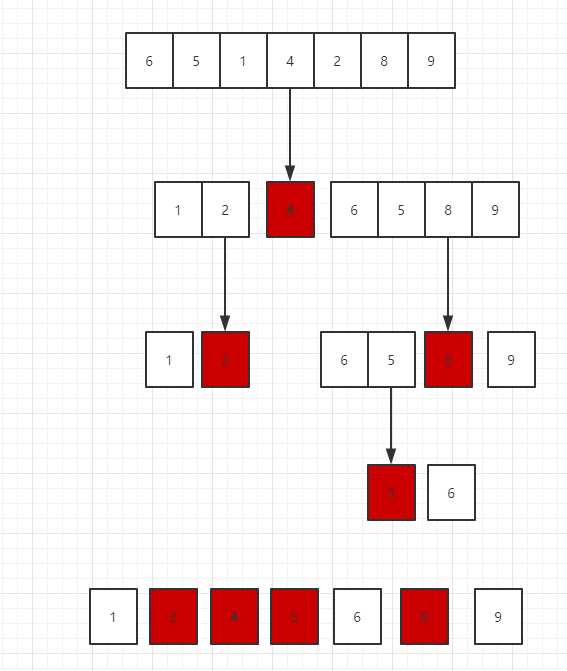
　　如上图，当我们把排序的任务分解到每一个小数组中，每个小数组有序了，那么整个大数组就有序了。因为分组过程中我们是根据和基数的比较大小分组的。

　　下面看一下java代码，先贴出一个 空间优化（在当前arr中操作）的代码。

 /** 
    * @Description: 快速排序 
    * @Param: [arr, start, end] 
    * @return: void 
    * @Author: fyp
    * @Date: 2018/4/9 
    */ 
    private static void sort(int[] arr,int start,int end){
        if(arr.length<=1){
           return;
        }

        int smallIndex = partition(arr,start,end);
        if (smallIndex > start){
            sort(arr,start,smallIndex - 1);
        }
        if (smallIndex < end){
            sort(arr,smallIndex + 1,end);
        }
    }

    /**
    * @Description: 将数组根据中间索引分组 小的放在左边，大的放在右边
    * @Param: [arr, midIndex]
    * @return: void
    * @Author: fyp
    * @Date: 2018/4/9
    */
    private static int partition(int[] arr,int start,int end) {
        //基准值取中间的值
        int pivot = start + (end - start) / 2;

        int smallIndex = start - 1;
        //先将基准值放到数组最后一个位置
        swap(arr, pivot, end);

        for (int i = start; i <= end; i++) {
            //如果当前值小于基准值（此时基准值 = arr[end]）,最小索引加1
            if (arr[i] <= arr[end]) {
                smallIndex++;
                if (i > smallIndex) {
                    //将当前索引位置的值和最小索引位置的值互换，保证小值都在左边
                    swap(arr, i, smallIndex);
                }
            }
        }
        return smallIndex;
    }
    
    /** 
    * @Description: 数组内两个数交换
    * @Param: [arr, i, j] 
    * @return: void 
    * @Author: fyp
    * @Date: 2018/4/9 
    */ 
    private static void swap(int[] arr,int i,int j){
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

　　中间的partition利用了一些小思路进行数组元素替换。首先将基数放到最后，然后小于基数的值就替换到前边的索引（smallIndex）上。依次类推，最后基数也（可能）会替换到中间去。

　　下面看一下程序运行打印结果：（运行结果和上图中的标红的元素有出入，不过基本思路是一致的）

　　

总结

　　快速排序的时间复杂度为 O(nlogN) .因为每一层需要对 N 个元素操作。而操作栈的深度为 logN（最好情况下)，所以时间复杂度为  O(n) * O(logN) = O(nlogN)，以上就是本问内容，你看懂了吗？