计组_IEEE754_练习题

Posted 2020-07-09 Jason333

IEEE754   阶码：移码；尾数：原码

一个规格化的32位浮点数x的真值可表示为：

         x=(－1)^s×(1. M) × 2^(E－127)       e=E－127

其中尾数域所表示的值是1. M。因为规格化的浮点数的尾数域最左位（最高有效位）总是1。故这一位经常不予存储，而认为隐藏在小数点的左边。

 

 

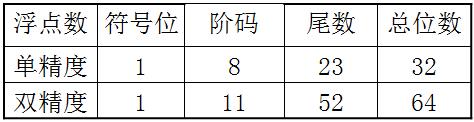
64位的浮点数中符号位1位，阶码域11位，尾数域52位，指数偏移值是1023。因此规格化的64位浮点数x的真值为：

         x=(－1)^s ×(1.M) × 2^(E－1023)     e=E－1023

 

 

IEEE754练习题：
1、将十进制数178.125表示成微机中的单精度浮点数。

　　解:178.125=10110010.001B

          　　        =1.0110010001×2^7 

　　 指数E=7+127=134=10000110B 

　　127是单精度浮点数应加的指数偏移量，其完整的浮点数形式为：

　　 0   10000110   011 0010 0010 0000 0000 0000

 　　 = 43322000H

2、将下面Pentium机中的单精度浮点数表示成十进制真值是多少？
0011 ,1111,0101,1000,0000,0000,0000,0000 

　　解：0011 ,1111,0101,1000,0000,0000,0000,0000

　　数符:S=(-1) 0=1   （正号）

　　阶码: E=(01111110)2-127=126-127= -1

　　尾数: D=(1.1011)2

   　　 X= 1.1011×2-1= (0.11011)2=0.84375