1. 参数VS非参数
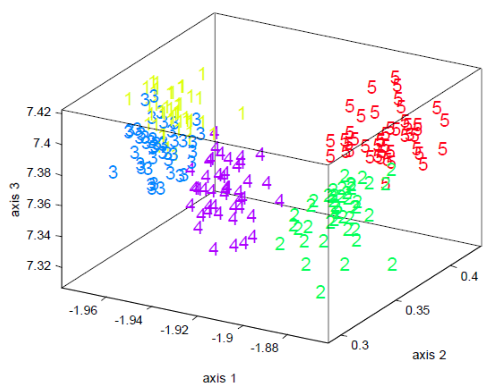
给定样本集 $(x_i, y_i), i= 1,2,\cdots, n $,其中 \(x_i\) 表示特征向量， \(y_i\) 表示样本标签。
考虑一个新的向量 \(x\)，要将他分类到可选分类 \({C_1, C_2,\cdots, C_c}\)中 。
方法：
- 参数的
- 非参数的
1.1 参数方法
参数方法：
参数方法假设样本分布的形式(概率密度函数Probability Density Function)是已知的
使用训练样本来估计分布参数，比如高斯分布中的 \(\mu\) 和 \(\sigma\)
如果对于分布的假设是正确的，则预测会很准确；否则预测可能会很差
?
参数方法使用极大似然估计来训练分类器，这点在前面一章的贝叶斯决策论也讲过。
假定：
- 给定训练集 \(D=(x_k, y_k), k=1,2,\cdots,n\)
- \(p(x|\omega_i)\sim N(\mu_i, \Sigma_i), i=1,2,\cdots, c\)
方法：
- 将训练集 \(D\) 划分为 \(D_i,i=1,2,\cdots, c\)
- 对每一个分类的数据 \(D_i\) 分别估计 \(\mu_i\) 和 \(\Sigma_i\)
- 判别函数 \(g_i(x)\) 取决于 \(\mu_i\) 和 \(\Sigma_i\)
\[ \begin{align} \hat{\mu}&=\frac{1}{n}\sum_{k=1}^nx_k, & \hat{\sigma}^2=\frac{1}{n}\sum_{k=1}^n(x_k-\hat{\mu})^2 \end{align} \]
1.2 非参数方法
非参数方法：
- 不会去假设样本分布符合某种特定分布
- 相反，它假设判别函数具有某种特定的形式。比如SVM ，神经网络等等
- 训练样本被用来估计分类器的参数
- 局部最优，但易于使用
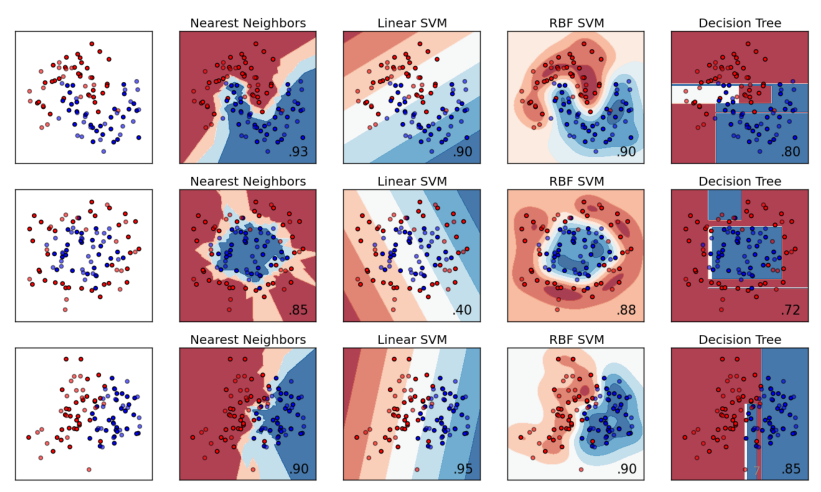
2. 线性分类模型(二分类为例)
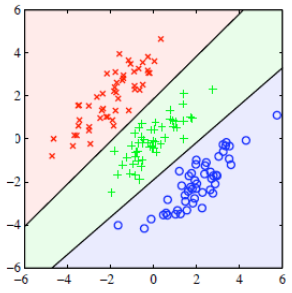{:width="100px"}
考虑一个简单的场景：类之间不相交
- 数据线性可分
- 不同类的数据由一个线性决策表面完全分开
线性判别式注意：
- 决策表面是输入的线性函数
- 输入空间划分为决策区域
2.1 二分类问题
决策表面如此定义 \(g(x)=0\):
\[
\begin{align}
g(x)=w^Tx+w_0
\end{align}
\]
因为 \(g(x)\) 是线性的，所以决策表面是一个超平面：
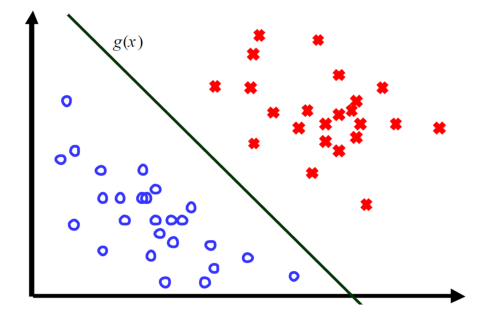
2.1.1 线性判别函数的几何意义
对于一个2分类线性判别函数：
- 判别函数表示向量\(x\)(代表一个待分类的数据)各个分量的线性组合，公式(2)已经说明了这个问题
- \(g(x)=w^Tx+w_0\)，其中 \(w\) 和 \(w_0\) 表示权重向量和偏置
- 对于一个给定的 \(x\)，若 \(g(x)\geq0\) ,则 \(x\in C_1\) ，否则 \(x\in C_2\)
- 决策边界 \(g(x)=0\)
几何意义：任意点到决策表面的距离
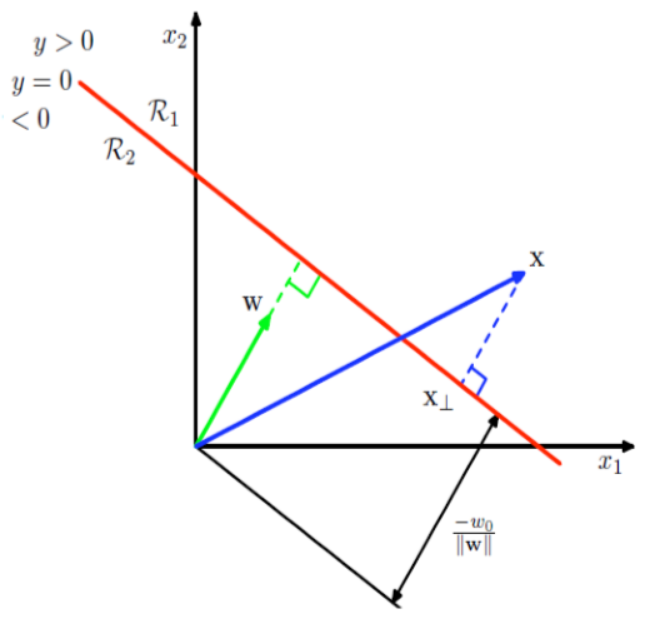
令 \(x\) 为任意点
令 \(x_\perp\)表示 \(x\) 到决策表面的正交投影
?
\[
\notag x=x_\perp + r\frac{w}{||w||} \text { where } r \text{ denote the distance between } x_\perp \text{ and } x
\]
- 两边都乘以相同的因子 \(w^T\),则:
\[ \notag g(x)=0+\frac{r}{||w||}\Rightarrow r=\frac{g(x)}{||w||} \]
2.2 决策区域的凸性
简单的说，就是两个点 \(x_a\) 和 \(x_b\)在区域 \(R_k\)中，则两点连线上的所有点，均在这个区域内。
2.3 向量增强
对公式(2)如下操作：
- 增加一维 \(x_0=1\)
- \(x \leftarrow (x_0,x)\)
- \(w\leftarrow (\omega_0, w)\)
于是:
\[
g(x)=w^Tx
\]
显然这个决策边界在增强的 \(D+1\) 维样本空间中穿过原点
2.4 模型小结
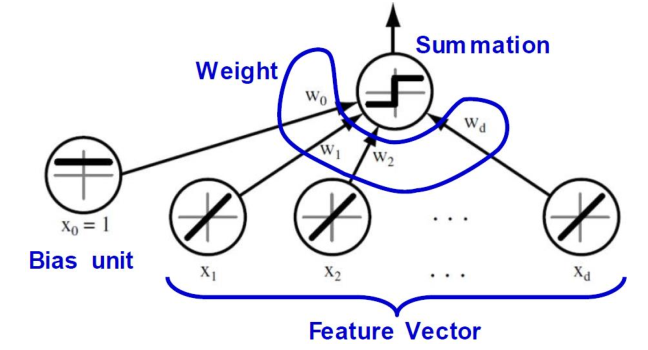
- 判别函数表示向量\(x\)(代表一个待分类的数据)各个分量的线性组合，视作每个独立单元
- 每个单元都具有输入输出
- 输入单元精确输出与输入相同的值
- 如果加权输入之和大于0，则输出单元输出1，否则输出-1
2.5 感知器算法
输入向量 \(x\) 通过一个固定的非线性变化得到一个特征向量 \(\phi(x)\)
\[
\notag g(x)=f(w^T\phi(x))
\]
\(f\) 是一个符号函数
\[
\notag f(a)=\left\{
\begin{array} {ll}
+1,a\geq0\-1, a<0
\end{array}
\right.
\]
+1和-1分别表示向量 \(x\) 属于两个类。根据这个设定，我们可以得到损失函数。
2.5.1 感知器标准
使用标签 \(y_n\in\{+1,-1\}\)，每个模式需要满足:
\[
\notag w^T\phi(x_n)y_n>0
\]
对每个分错的样本，感知器标准试图最小化:
\[
E(w)=-w^T\phi(x_n)y_n
\]
2.5.2 算法流程
随机梯度下降梯度更新公式:
\[
\begin{array}{ll}
w^{k+1}&=w^k-\eta\nabla E(w)\&=w^k+\eta\phi(x_n)y_n
\end{array}
\]
其中，\(\eta\) 是学习率，\(k\) 是steps
算法训练循环以下步骤：
- 如果样本错分为\(C_1(y_n=+1)\)，增加权重
- 如果样本错分为\(C_2(y_n=-1)\)，减小权重
2.6 最小二乘分类
主要思想，最小化投影距离：
\[
J_s(w)=\sum_{i=1}^n(w^Tx_i-b_i)^2
\]
其中 \(b_i\) 是任意选取的。
对公式(6)进一步化简:
\[
J_s(w)=||Xw-b||^2
\]
其中矩阵符号:
\[
\notag w=\begin{pmatrix}
w_0 \\ w_1 \\ \vdots \\ w_d
\end{pmatrix},X=\begin{pmatrix}
x_{10} &x_{11} & \cdots &x_{1d} \\
x_{20}&x_{21} & \cdots & x_{2d}\ \vdots & \vdots & \ddots & \vdots \\
x_{n0}& x_{n1} & \cdots & x_{nd}
\end{pmatrix},b=\begin{pmatrix}
b_0 \\ b_1 \\ \vdots \\ b_d
\end{pmatrix}
\]
最小化 \(J\), 显然 \(Xw=b\)，所以有：
\[
\notag w = X^{-1}b
\]
然而，矩阵 \(X\) 可能是奇异的，也就是说，没有逆矩阵。
2.6.1 违逆法pseudo-inverse method
对于公式(7)，求梯度：
\[
\notag \nabla J_s(w)=2X^T(Xw-b)
\]
极值必要条件：
\[
\notag X^TXw=X^Tb
\]
可以求得：
\[
w=(X^TX)^{-1}X^Tb
\]
2.6.2 最小均方算法least-Mean-Squared
相比于违逆法，该方法的优势在于
- 违逆法在 \(X^TX\) 奇异的时候有问题
- 避免了矩阵很大的时候计算复杂
- 违逆法训练时间更长
回顾公式(6)，直接求其对于\(w\)的梯度：
\[
\notag \nabla J_s(w)=2\sum_{i=1}^n(w^Tx_i-b_i)x_i
\]
更新公式：
\[
w(k+1)=w(k)+\eta(k)(b_i-w^Tx_i)x_i
\]
- 即使分离超平面存在，LMS方法也不需要收敛到它
- 由于梯度噪声，LMS不会达到最佳效果
2.7 广义线性模型
广义线性判别函数：
\[
g(x)=f(w^Tx+\omega_0)
\]
其中 \(f\) 是激活函数。相应的决策表面：
\[
\notag g(x)=\text{constant Or }w^Tx+\omega_0=\text{constant}
\]
所以决策边界在特征空间里是线性的，即使 \(f\) 是非线性的
广义线性判别函数：
\[
\notag g(x)=\sum_{i=1}^nw_i\phi_ix
\]
二次判别函数：
\[
\notag \begin{array}
g(x)=w_0+w_ix+w_2x^2\\text{where } \phi_1(x)=1,\phi_2(x)=x,\phi_3(x)=x^2
\end{array}
\]
对于样本 \(x_i\)，如果分类正确，则 \(g(w,x_i)y_i>0\)
定义一个判别函数 \(J(w)\),如果 \(w\)是一个解向量，则该函数达到最小值
算法流程：
随机选择初始权重 \(w_1\)
计算梯度 \(\nabla J(w(1))\)
根据负梯度计算：
\[ \notag w(k+1)=w(k)-\eta(k)\nabla J(w(k)) \text{ for }\nabla J=\frac{\partial J}{\partial w} \]
\(\eta\) 是学习率，控制步幅
3.多分类
3.1 扩展到多分类方法
- One-versus-the-rest
构建判别函数，使用 \(c\) 个分类器，每个分类器解决一个2分类问题
- One-versus-one
\(c\) 个分类，对每两个分类构建一个分类器，则共有 \(\frac{c(c-1)}{2}\) 个判别函数
3.2 多分类判别
考虑一个 \(c\) 分类问题，判别函数形式：
\[
\notag y_k(x)=w_k^Tx+w_{k0}
\]
对于给定输入 \(x\)，如果 \(y_k(x)>y_j(x) \text{ for all }j\neq k\)，则 \(x\in C_k\)，则 \(C_k\) 和 \(C_j\)之间的决策边界为：
\[
\notag y_k(x)=y_j(x)
\]
相应的超平面为：
\[
\notag (w_k-w_j)^Tx +(\omega_{k0}-\omega_{j0})=0
\]
二分类问题其实也是如此。
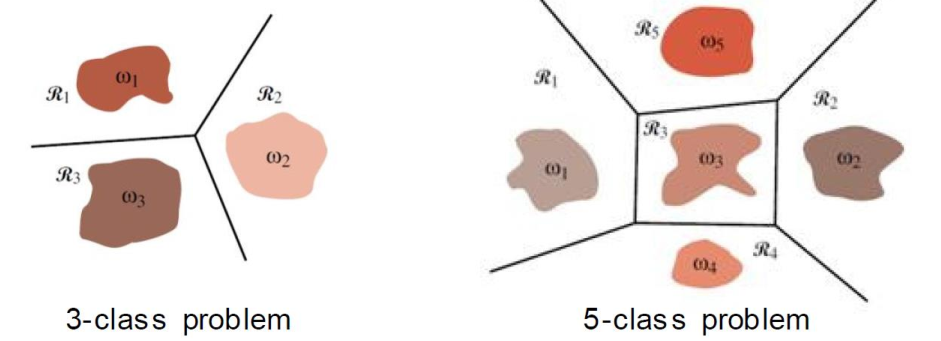
优势：
- 避免默认两可的区域
- 每个决策区域单连通
- 低复杂度
- 需要c个分类器