题目描述
参与考古挖掘的小明得到了一份藏宝图,藏宝图上标出了 n 个深埋在地下的宝藏屋, 也给出了这 n 个宝藏屋之间可供开发的 m 条道路和它们的长度。
小明决心亲自前往挖掘所有宝藏屋中的宝藏。但是,每个宝藏屋距离地面都很远, 也就是说,从地面打通一条到某个宝藏屋的道路是很困难的,而开发宝藏屋之间的道路 则相对容易很多。
小明的决心感动了考古挖掘的赞助商,赞助商决定免费赞助他打通一条从地面到某 个宝藏屋的通道,通往哪个宝藏屋则由小明来决定。
在此基础上,小明还需要考虑如何开凿宝藏屋之间的道路。已经开凿出的道路可以 任意通行不消耗代价。每开凿出一条新道路,小明就会与考古队一起挖掘出由该条道路 所能到达的宝藏屋的宝藏。另外,小明不想开发无用道路,即两个已经被挖掘过的宝藏 屋之间的道路无需再开发。
新开发一条道路的代价是:
L×K
L代表这条道路的长度,K代表从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的 宝藏屋的数量(包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋) 。
请你编写程序为小明选定由赞助商打通的宝藏屋和之后开凿的道路,使得工程总代 价最小,并输出这个最小值。
思路
首先,肯定能发现应该是要枚举每一个点作为起点,然后计算最小值,但是怎么计算最小值就是成了一个问题(╯▔皿▔)╯
注意到n小于等于12,能联想到状压dp,另外,题目中给的m小于等于1000其实是没有什么卵用的2333333,因为最优情况下应该是一个树形结构,所以开始应该先处理好边,排序后选最小值。
另外,我们大概能想到dp的状态应该是每个藏宝屋是否到达过。但是,题目中描述每个藏宝屋到根节点的路径上的藏宝屋个数不同,所需的价值也就不同,所以这一维dp肯定是不够用的,还需要一维状态来表示到根节点的距离,所以dp[i][j]的意义就是当前在树的第i层,到的屋子状态为j时的最小代价。然后进行暴力枚举即可(●‘?‘●)
步骤
1.首先用最基本的贪心思想来保留两点之间权值最小的道路。
2.枚举一个点到一个集合的最小代价
3.借用第二步中的数据来计算一个集合到另一个集合的最小代价
4.进行dp
正确性证明
枚举dp时首先枚举当前层数,然后枚举当前状态,然后枚举下一步的状态,进行转移。
但是!!! (╯‵□′)╯︵┻━┻
在状态转移时不能保证下一层的所有房子道路全部都连接在这一层中,因为在贪心时只知道这个房子的集合到另一个集合的最小代价,而此时并不知道练到的是第几层的房子,那么应该怎么证明呢??( ̄_, ̄ )
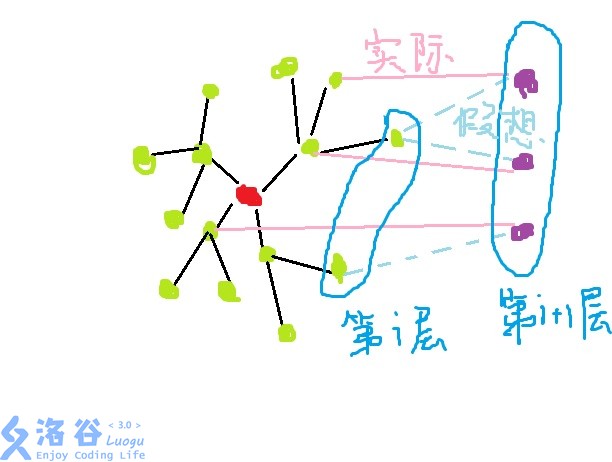
即使当前的连接方式不是正确的,但是计算的时候还是按连接在i来计算的,因为每次都枚举了所有的情况,所以在前面的时候已经枚举过了这种情况,并且乘的层数要比当前小,因此不会漏过最佳答案qwq
代码
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 long long dp[15][1<<13]; 7 long long dj[15][1<<13],jj[1<<13][1<<13]; 8 long long dis[15][15]; 9 const long long INF=9999999999999LL; 10 int main(){ 11 for(register int i=0;i<=14;i++){ 12 for(register int j=0;j<=14;j++){ 13 if(i!=j)dis[i][j]=INF; 14 } 15 } 16 int n,m; 17 cin>>n>>m; 18 long long tot=(1<<n)-1; 19 for(register int i=1;i<=m;i++){ 20 register int f,t,v; 21 scanf("%d%d%d",&f,&t,&v); 22 dis[f][t]=min(dis[f][t],(long long)v); 23 dis[t][f]=min(dis[t][f],(long long)v); 24 } 25 for(register int i=1;i<=n;i++){ 26 for(register int j=0;j<=tot;j++){ 27 dj[i][j]=INF; 28 } 29 } 30 31 for(register int i=0;i<=tot;i++){ 32 for(register int j=0;j<=tot;j++){ 33 jj[i][j]=INF; 34 } 35 } 36 37 //dian dao ji he 38 39 for(register int i=1;i<=n;i++){ 40 for(register int j=0;j<=tot;j++){ 41 for(register int k=1;k<=n;k++){ 42 if(j&(1<<(k-1))){ 43 dj[i][j]=min(dj[i][j],dis[i][k]); 44 } 45 } 46 } 47 } 48 49 //ji he dao ji he 50 for(register int i=0;i<=tot;i++){ // mei ju di yi ge ji he 51 int C=tot^i; //ji suan bu ji 52 for(register int j=C;j;j=(j-1)&C){ 53 long long xx=0; 54 for(register int k=1;k<=n;k++){ 55 if((j|(1<<(k-1)))==j){ 56 xx+=dj[k][i]; 57 } 58 } 59 if(xx<INF){ 60 jj[j][i]=xx; 61 } 62 else jj[j][i]=INF; 63 } 64 } 65 //jin xing dp 66 long long ans=999999999; 67 for(register int root=1;root<=n;root++){ 68 //chu shi hua 69 for(register int j=0;j<=n;j++){ 70 for(register int k=0;k<=tot;k++){ 71 dp[j][k]=INF; 72 } 73 } 74 dp[0][(1<<(root-1))]=0; 75 for(register int i=0;i<n;i++){ // 枚举层数 76 for(register int j=0;j<=tot;j++){ //mei ju dang qian zhuang tai 77 if(dp[i][j]==INF)continue; 78 int C=tot^j; //ji suan bu ji 79 for(register int k=0;k<=tot;k++){ 80 if((k|C)==C){ 81 dp[i+1][k|j]=min(dp[i+1][k|j],dp[i][j]+jj[k][j]*(i+1)); 82 } 83 } 84 } 85 } 86 for(register int i=0;i<=n;i++){ 87 ans=min(ans,dp[i][tot]); 88 } 89 } 90 cout<<ans<<endl; 91 }