[Code Plus#4] 最短路

Posted 2020-10-29 蒟蒻JHY

题目背景

在北纬 91° ，有一个神奇的国度，叫做企鹅国。这里的企鹅也有自己发达的文明，称为企鹅文明。因为企鹅只有黑白两种颜色，所以他们的数学也是以二进制为基础发展的。

比如早在 1110100111101001 年前，他们就有了异或这样一个数学概念。如果你不知道异或是什么，请出门过墙左转到这里。

再比如早在 10000101000010 年前，他们的大科学家 Penguin. Tu 就提出了图和最短路径这样一些概念。

题目描述

企鹅国中有 NN 座城市，编号从 11 到 NN 。

对于任意的两座城市 ii 和 jj ，企鹅们可以花费 (i~\\mathrm{xor}~j) \\times C(i xor j)×C 的时间从城市 ii 走到城市 jj ，这里 CC 为一个给定的常数。

当然除此之外还有 MM 条单向的快捷通道，第 ii 条快捷通道从第 F_iFi​ ​​ 个城市通向第 T_iTi​ ​​ 个城市，走这条通道需要消耗 V_iVi​ ​​ 的时间。

现在来自 Penguin Kingdom University 的企鹅豆豆正在考虑从城市 AA 前往城市 BB 最少需要多少时间？

输入输出格式

输入格式：

 

从标准输入读入数据。

输入第一行包含三个整数 N,M,CN,M,C ，表示企鹅国城市的个数、快捷通道的个数以及题面中提到的给定的常数CC 。

接下来的 MM 行，每行三个正整数 F_i,T_i,V_iFi​,Ti​,Vi​ ​ (1 \\leq F_i \\leq N1≤Fi​≤N ,1 \\leq T_i \\leq N ,1\\leq V_i \\leq 1001≤Ti​≤N,1≤Vi​≤100 )，分别表示对应通道的起点城市标号、终点城市标号和通过这条通道需要消耗的时间。

最后一行两个正整数 A,BA,B (1 \\leq C \\leq 100)(1≤C≤100) ，表示企鹅豆豆选择的起点城市标号和终点城市标号。

 

输出格式：

 

输出到标准输出。

输出一行一个整数，表示从城市 AA 前往城市 BB 需要的最少时间。

 

输入输出样例

输入样例#1： 

4 2 1
1 3 1
2 4 4
1 4

输出样例#1： 

5

输入样例#2： 

7 2 10
1 3 1
2 4 4
3 6

输出样例#2： 

34

说明

样例1解释

直接从 11 走到 44 就好了。

样例2解释

先从 33 走到 22 ，再从 22 通过通道到达 44 ，再从 44 走到 66 。

 

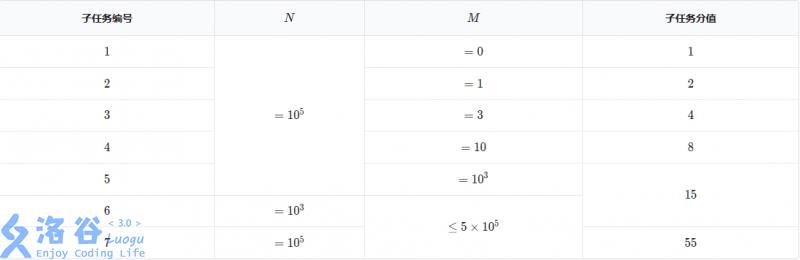
活泼可爱的出题人给大家留下了下面这张图。

Credit: https://www.luogu.org/discuss/show/38908

 

 

    如果暴力把图建出来的话，边的级别是O(N^2)的，肯定不行。。。暴力的局限在于没有用到异或的特殊性

    如果我们从一个点i，每次直走到变某一位的点，最后走到j，那么满足至少存在一条 边权和= i xor j的路径，这个是比较显然的。

    所以我们把这个图建出来然后再直接跑最短路就好啦。

但是要注意，要把n补到 2^i-1，因为有一些中间点会>n。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=200005;
int ci[33],n,m,d[maxn],val[maxn*37],C,S,T;
int hd[maxn],to[maxn*37],ne[maxn*37],num;
bool v[maxn];
struct node{
	int x,dis;
	bool operator <(const node &u)const{
		return dis>u.dis;
	}
};
priority_queue<node> q;

inline void add(int u,int v,int w){
	to[++num]=v,ne[num]=hd[u],hd[u]=num,val[num]=w;
}

inline void dij(){
	memset(d,0x3f,sizeof(d));
	d[S]=0,q.push((node){S,0});
	node x;
	
	while(!q.empty()){
		x=q.top(),q.pop();
		if(v[x.x]) continue;
		
		v[x.x]=1;
		for(int i=hd[x.x];i;i=ne[i]) if(d[x.x]+val[i]<d[to[i]]){
			d[to[i]]=d[x.x]+val[i];
			q.push((node){to[i],d[to[i]]});
		}
	}
	
	printf("%d\\n",d[T]);
}

int main(){
	ci[0]=1;
	for(int i=1;i<=20;i++) ci[i]=ci[i-1]<<1;
	
	scanf("%d%d%d",&n,&m,&C);
	int uu,vv,ww;
	for(int i=1;i<=m;i++){
		scanf("%d%d%d",&uu,&vv,&ww);
		add(uu,vv,ww);
	}
	scanf("%d%d",&S,&T);
	
	int U=n;
	for(n=1;n<=U;n<<=1);
	n--;
	
	for(int L=0;ci[L]<=n;L++)
	    for(int i=1,TO;i<=n;i++){
	    	TO=i^ci[L];
	    	if(TO) add(i,TO,ci[L]*C);
		}
		
	dij();
	
	return 0;
}