题意:给一棵带边权的树,多次询问$(x,y,l)$表示如果加一条连接$x$和$y$的长为$l$的边,所有点到$x$和到$y$的最短路减少了多少
先把题目中的图放上来(雾

考虑用lct维护,先把路径提出来,然后在splay上二分找到最短路大小改变的临界点$p$,再统计答案
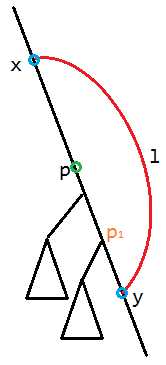
容易看出$p\\rightarrow y$上的所有点的子树都对答案有贡献,对于一个点$p_1$,它和它的虚子树对答案的贡献都是$dis_{x,p_1}-dis_{p_1,y}-l$,即$dis_{x,y}-2dis_{p_1,y}-l$,于是我们可以维护每个点在splay中往左往右的答案(因为要换根,有区间翻转操作),再维护一下虚子树大小即可
车万题吼啊!
#include<stdio.h>
#include<string.h>
typedef long long ll;
template<class C>void swap(C&a,C&b){a^=b^=a^=b;}
int ch[100010][2],fa[100010],r[100010],siz[100010],vsiz[100010];
ll lsum[100010],rsum[100010],s[100010],v[100010];
#define ls ch[x][0]
#define rs ch[x][1]
void rev(int x){
r[x]^=1;
swap(ls,rs);
swap(lsum[x],rsum[x]);
}
void pushdown(int x){
if(r[x]){
if(ls)rev(ls);
if(rs)rev(rs);
r[x]=0;
}
}
void pushup(int x){
siz[x]=siz[ls]+siz[rs]+vsiz[x];
s[x]=s[ls]+s[rs]+v[x];
lsum[x]=lsum[ls]+lsum[rs]+(s[ls]+v[x])*siz[rs]+vsiz[x]*s[ls];
rsum[x]=rsum[ls]+rsum[rs]+(s[rs]+v[x])*siz[ls]+vsiz[x]*s[rs];
}
void rot(int x){
int y,z,f,b;
y=fa[x];
z=fa[y];
f=ch[y][0]==x;
b=ch[x][f];
fa[x]=z;
fa[y]=x;
if(b)fa[b]=y;
ch[x][f]=y;
ch[y][f^1]=b;
if(ch[z][0]==y)ch[z][0]=x;
if(ch[z][1]==y)ch[z][1]=x;
pushup(y);
pushup(x);
}
bool isrt(int x){return ch[fa[x]][0]!=x&&ch[fa[x]][1]!=x;}
void gao(int x){
if(!isrt(x))gao(fa[x]);
pushdown(x);
}
void splay(int x){
gao(x);
int y,z;
while(!isrt(x)){
y=fa[x];
z=fa[y];
if(!isrt(y))rot((ch[z][0]==y&&ch[y][0]==x)||(ch[z][1]==y&&ch[y][1]==x)?y:x);
rot(x);
}
}
void access(int x){
int y=0;
while(x){
splay(x);
vsiz[x]+=siz[rs];
rs=y;
vsiz[x]-=siz[y];
pushup(x);
y=x;
x=fa[x];
}
}
void makert(int x){
access(x);
splay(x);
rev(x);
}
int find(int x,ll d){
int c=0;
ll al=s[x];
while(x){
pushdown(x);
if((s[ls]+v[x])*2<=al+d){
c=x;
d-=(s[ls]+v[x])*2;
x=rs;
}else
x=ls;
}
return c;
}
ll query(int x,int y,ll z){
if(x==y)return 0;
makert(x);
access(y);
splay(y);
if(s[y]<=z)return 0;
x=find(y,z);
splay(x);
return siz[rs]*(s[x]-z)-rsum[rs]*2;
}
int h[100010],nex[200010],to[200010],M;
void add(int a,int b){
M++;
to[M]=b;
nex[M]=h[a];
h[a]=M;
}
void dfs(int x){
for(int i=h[x];i;i=nex[i]){
if(to[i]!=fa[x]){
fa[to[i]]=x;
dfs(to[i]);
siz[x]+=siz[to[i]];
}
}
vsiz[x]=siz[x];
}
int main(){
int n,m,i,x,y,z;
while(~scanf("%d",&n)){
memset(h,0,sizeof(h));
memset(fa,0,sizeof(fa));
memset(ch,0,sizeof(ch));
memset(siz,0,sizeof(siz));
memset(r,0,sizeof(r));
memset(lsum,0,sizeof(lsum));
memset(rsum,0,sizeof(rsum));
memset(s,0,sizeof(s));
memset(v,0,sizeof(v));
M=0;
for(i=1;i<=n;i++)siz[i]=1;
for(i=1;i<n;i++){
scanf("%d%d%d",&x,&y,&z);
v[n+i]=s[n+i]=z;
add(x,n+i);
add(n+i,x);
add(y,n+i);
add(n+i,y);
}
dfs(1);
scanf("%d",&m);
while(m--){
scanf("%d%d%d",&x,&y,&z);
printf("%lld\\n",query(x,y,z)+query(y,x,z));
}
}
}