测评中的编程题组合数相关的问题

Posted 2020-10-29 xiao-gan

最近做测评的过程中碰到两类求组合数的问题：

1. 求组合数的值的大小

2. 求组合数的排列情况

下面分别来讨论

1. 求组合数的值的大小

^{第一种最直接能想到的办法，就是用排列组合公式}

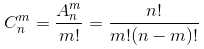
这样求固然很快，但是无法对中间值进行操作。换句话说，最后求得的结果会很大，可能导致溢出。

当需要对中间值进行操作的时候，如对进行中间值取模操作，就可以用下面的方法。

第二种方法，利用关系式逐层推导

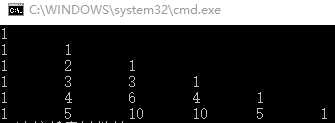
 1 int zuhe(int n, int m)
 2 {
 3     if (n < m)
 4         return zuhe(m, n);
 5     vector<vector<int>> v(n + 1, vector<int>(n + 1, 0));
 6     for (int i = 0;i <= n;i++)
 7         v[i][0] = 1;    //第0列的初始值为1，C(n,0)也返回1
 8     cout << 1 << endl;
 9     for (int i = 1;i <= n;i++)
10     {
11         cout << 1;
12         for (int j = 1;j <= i;j++)
13         {
14             v[i][j] = v[i - 1][j] + v[i - 1][j - 1];
15             cout << ‘    ‘ << v[i][j];
16         }
17         cout << endl;
18     }
19     return v[n][m];
20 }

以C(5,2)为例，打印出如下的表，在每一步的计算过程中都可以进行取模操作，不用担心最后结果会非常大。

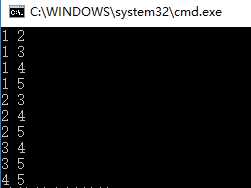
2. 求组合数的排列情况

思路：利用递归，类似dfs

 1 void help(int n, int m, set<int> s = set<int>(), int cnt = 0, int from = 1)
 2 {
 3     if (cnt == m)
 4     {
 5         for (auto item : s)
 6             cout << item << ‘ ‘;
 7         cout << endl;
 8         return;
 9     }
10     else
11     {
12         for (int i = from;i <= n;i++)
13         {
14             if (s.find(i) == s.end())
15             {
16                 s.insert(i);
17                 help(n, m, s, cnt + 1, i + 1);    //cnt表示set中加入数字的数量（递归轮数），from表示下一轮递归从数字几开始
18                 s.erase(i);
19             }
20         }
21     }
22 }

同样以C(5,2)为例，输出结果如下