机器学习--层次聚类从初识到应用

Posted 2020-10-29 L先生AI课堂

一、前述

聚类就是对大量未知标注的数据集，按数据的内在相似性将数据集划分为多个类别，使类别内的数据相似度较大而类别间的数据相似度较小.

数据聚类算法可以分为结构性或者分散性,许多聚类算法在执行之前，需要指定从输入数据集中产生的分类个数。

1.分散式聚类算法，是一次性确定要产生的类别，这种算法也已应用于从下至上聚类算法。

2.结构性算法利用以前成功使用过的聚类器进行分类，而分散型算法则是一次确定所有分类。

结构性算法可以从上至下或者从下至上双向进行计算。从下至上算法从每个对象作为单独分类开始，不断融合其中相近的对象。而从上至下算法则是把所有对象作为一个整体分类，然后逐渐分小。

3.基于密度的聚类算法，是为了挖掘有任意形状特性的类别而发明的。此算法把一个类别视为数据集中大于某阈值的一个区域。DBSCAN和OPTICS是两个典型的算法。

4.层次聚类，是一种很直观的算法。顾名思义就是要一层一层地进行聚类，可以由上向下把大的类别（cluster）分割，叫作分裂法；也可以由下向上对小的类别进行聚合，叫作凝聚法；但是一般用的比较多的是由下向上的凝聚方法。

二、具体

1、大致过程：

层次聚类方法对给定的数据集进行层次的分解，直到某种条件满足为止。
在已经得到距离值之后，元素间可以被联系起来。通过分离和融合可以构建一个结构。传统上，表示的方法是树形数据结构，

层次聚类算法，要么是自底向上聚集型的，即从叶子节点开始，最终汇聚到根节点；要么是自顶向下分裂型的，即从根节点开始，递归的向下分裂。

 

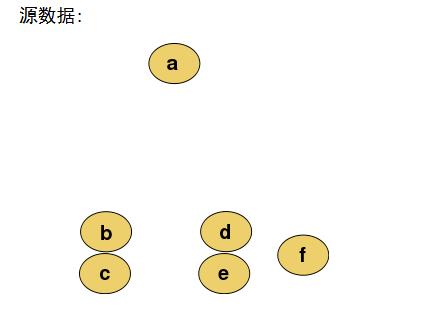
2、凝聚层次聚类：

首先将每个对象作为一个簇，然后合并这些原子簇为越来越大的簇，直到某个终结条件被满足。

AGNES算法(自底向上)（用的多些）

所谓从下而上地合并cluster，具体而言，就是每次找到距离最短的两个cluster，然后进行合并成一个大的cluster，直到全部合并为一个cluster。

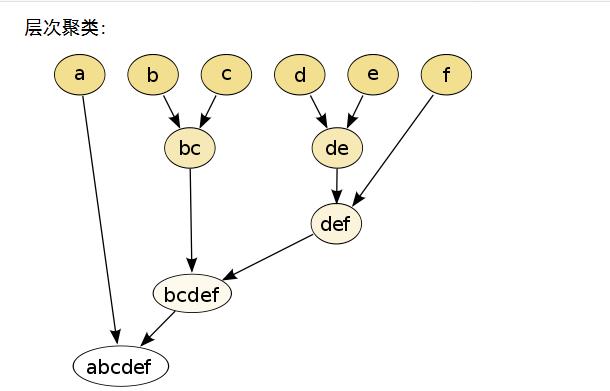
整个过程就是建立一个树结构，类似于下图。

一开始每个数据点独自作为一个类，它们的距离就是这两个点之间的距离。而对于包含不止一个数据点的cluster，就可以选择多种方法了。最常用的，就是average-linkage，即计算两个cluster各自数据点的两两距离的平均值。

 

 

凝聚法指的是初始时将每个样本点当做一个类簇，所以原始类簇的大小等于样本点的个数，然后依据某种准则合并这些初始的类簇，直到达到某种条件或者达到设定的分类数目。

用算法描述：

       输入：样本集合D，聚类数目或者某个条件（一般是样本距离的阈值，这样就可不设置聚类数目）
       输出：聚类结果

举例如下：

在平面上有6个点：p0(1,1), p1(1,2), p2(2,2), p3(4,4), p4(4,5), p5(5,6)，我现在需要对这6个点进行聚类，对应着上边的步骤我可以这样做：

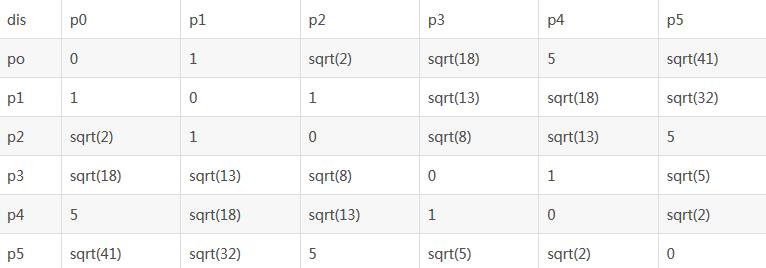
      1.首先每个样本看作是一个类簇，这样我可以得到初始的类簇有6个，分别为c1(p0),c2(p1),c3(p2),c4(p3),c5(p4),c6(p5)
       repeat：
       2.由上边的表可以得到两两类簇间的最小距离（并不是唯一，其他两个类簇间距离也可能等于最小值，但是先选取一个）是1，存在类簇c1和c2之间
       注意：这个类簇间距离的计算方法有许多种。
          (1).就是取两个类中距离最近的两个样本的距离作为这两个集合的距离，也就是说，最近两个样本之间的距离越小，这两个类之间的相似度就越大
          (2).取两个集合中距离最远的两个点的距离作为两个集合的距离
          (3).把两个集合中的点两两的距离全部放在一起求一个平均值，相对也能得到合适一点的结果。
          (4).取两两距离的中值，与取均值相比更加能够解除个别偏离样本对结果的干扰。
          (5).把两个集合中的点两两的距离全部放在一起求和然后除以两个集合中的元素个数
          (6).求每个集合的中心点(就是将集合中的所有元素的对应维度相加然后再除以元素个数得到的一个向量)，然后用中心点代替集合再去就集合间的距离

       3.合并类簇c1和c2,得到新的聚类结果c1(p0，p1),c3(p2),c4(p3),c5(p4),c6(p5)。
       util：若是我们要求聚成5个类别的话，我们这里就可以结束了。

    但是如果我们设定了一个阈值f，要求若存在距离小于阈值f的两个类簇时则将两个类簇合并并且继续迭代，我们又会回到repeat继续迭代从而得到新的聚类结果。

3、分裂层次聚类：

DIANA算法(自顶向下)

首先将所有对象置于一个簇中，然后逐渐细分为越来越小的簇，直到达到了某个终结条件。

分裂法指的是初始时将所有的样本归为一个类簇，然后依据某种准则进行逐渐的分裂，直到达到某种条件或者达到设定的分类数目。用算法描述：

    输入：样本集合D，聚类数目或者某个条件（一般是样本距离的阈值，这样就可不设置聚类数目）

    输出：聚类结果

    1.将样本集中的所有的样本归为一个类簇；

    repeat：

     2.在同一个类簇（计为c）中计算两两样本之间的距离，找出距离最远的两个样本a,b；

     3.将样本a，b分配到不同的类簇c1和c2中；

      4.计算原类簇（c）中剩余的其他样本点和a，b的距离，若是dis(a)<dis(b)，则将样本点归到c1中，否则归到c2中；

    util： 达到聚类的数目或者达到设定的条件