题目描述
小南有一套可爱的玩具小人, 它们各有不同的职业。
有一天, 这些玩具小人把小南的眼镜藏了起来。 小南发现玩具小人们围成了一个圈,它们有的面朝圈内,有的面朝圈外。如下图:
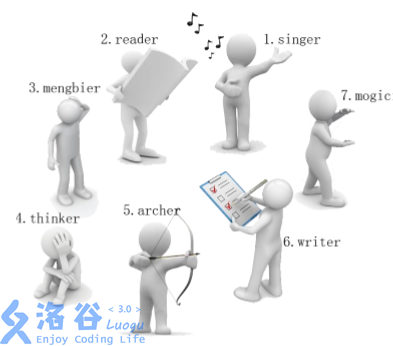
这时singer告诉小南一个谜題: “眼镜藏在我左数第3个玩具小人的右数第1个玩具小人的左数第2个玩具小人那里。 ”
小南发现, 这个谜题中玩具小人的朝向非常关键, 因为朝内和朝外的玩具小人的左右方向是相反的: 面朝圈内的玩具小人, 它的左边是顺时针方向, 右边是逆时针方向; 而面向圈外的玩具小人, 它的左边是逆时针方向, 右边是顺时针方向。
小南一边艰难地辨认着玩具小人, 一边数着:
singer朝内, 左数第3个是archer。
archer朝外,右数第1个是thinker。
thinker朝外, 左数第2个是writer。
所以眼镜藏在writer这里!
虽然成功找回了眼镜, 但小南并没有放心。 如果下次有更多的玩具小人藏他的眼镜, 或是谜題的长度更长, 他可能就无法找到眼镜了 。 所以小南希望你写程序帮他解决类似的谜題。 这样的谜題具体可以描述为:
有 n个玩具小人围成一圈, 已知它们的职业和朝向。现在第1个玩具小人告诉小南一个包含 m条指令的谜題, 其中第 z条指令形如“左数/右数第 s,个玩具小人”。 你需要输出依次数完这些指令后,到达的玩具小人的职业。
输入输出格式
输入格式:
输入的第一行包含两个正整数 n,m, 表示玩具小人的个数和指令的条数。
接下来 n行, 每行包含一个整数和一个字符串, 以逆时针为顺序给出每个玩具小人的朝向和职业。其中0表示朝向圈内, 1表示朝向圈外。保证不会出现其他的数。字符串长度不超过10且仅由小写字母构成, 字符串不为空, 并且字符串两两不同。 整数和字符串之问用一个空格隔开。
接下来 m行,其中第 z行包含两个整数 a,,s,,表示第 z条指令。若 a,= 0,表示向左数 s,个人;若a,= 1 ,表示向右数 s,个人。保证a,不会出现其他的数, 1≤ s,<n 。
输出格式:
输出一个字符串, 表示从第一个读入的小人开始, 依次数完 m条指令后到达的小人的职业。
输入输出样例
7 3 0 singer 0 reader 0 mengbier 1 thinker 1 archer 0 writer 1 mogician 0 3 1 1 0 2
writer
10 10 1 C 0 r 0 P 1 d 1 e 1 m 1 t 1 y 1 u 0 V 1 7 1 1 1 4 0 5 0 3 0 1 1 6 1 2 0 8 0 4
y
说明
【样例1说明】
这组数据就是【题目描述】 中提到的例子。
【子任务】
子任务会给出部分测试数据的特点。 如果你在解决题目中遇到了困难, 可以尝试只解决一部分测试数据。
每个测试点的数据规模及特点如下表:
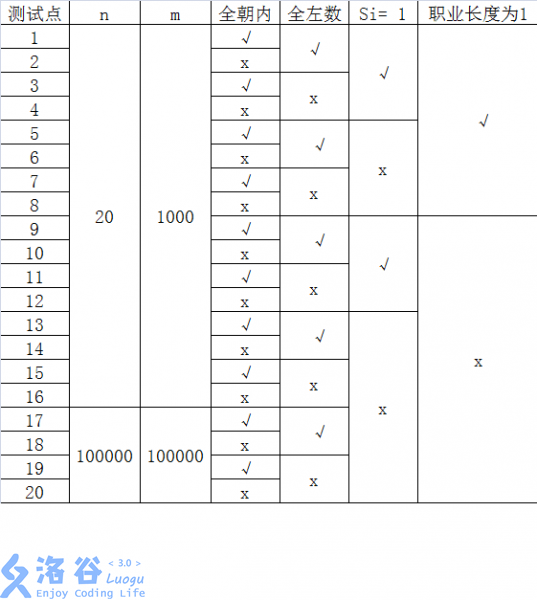
其中一些简写的列意义如下:
• 全朝内: 若为“√”, 表示该测试点保证所有的玩具小人都朝向圈内;
全左数:若为“√”,表示该测试点保证所有的指令都向左数,即对任意的
1≤z≤m, ai=0;
s,= 1:若为“√”,表示该测试点保证所有的指令都只数1个,即对任意的
1≤z≤m, si=1;
职业长度为1 :若为“√”,表示该测试点保证所有玩具小人的职业一定是一个
长度为1的字符串。
【代码】:

#include<bits/stdc++.h> using namespace std; #define eps 1e-6 #define ull unsigned long long #define N 100005 struct node { int face; string name; }a[N]; int main() { int n ,q; while(cin >> n >> q) { int op, s, now; for(int i=0; i<n; i++) { cin >> a[i].face >> a[i].name; } now = 0;//如果你这个从1存储,正好是最后一个怎么办 while( q-- ) //内右 = 外左 //%n会有结果为0的情况,然而你们都是从1开始的 { cin >> op >> s; //同为0 or 同为1 if(op ^ a[now].face == 0) now = (now-s+n)%n; //不断减少+n防止溢出 else now = (now+s)%n;; } cout<<a[now].name<<endl; } return 0; }
#include<bits/stdc++.h> using namespace std; #define eps 1e-6 #define ull unsigned long long #define N 100005 struct node { int face; string name; }a[N]; int main() { int n ,q; while(cin >> n >> q) { int op, s, now; for(int i=0; i<n; i++) { cin >> a[i].face >> a[i].name; } now = 0;//如果你这个从1存储,正好是最后一个怎么办 while( q-- ) //内右 = 外左 //%n会有结果为0的情况,然而你们都是从1开始的 { cin >> op >> s; //同为0 or 同为1 if(op ^ a[now].face == 0) now = (now-s+n)%n; //不断减少+n防止溢出 else now = (now+s+n)%n; } cout<<a[now].name<<endl; } return 0; }

#include<iostream> using namespace std; const int N=100005; int n,m,ans,dire,num; struct node{ bool face; string na; }pre[N]; //存面朝的方向和名字 int main() { cin>>n>>m; for(int i=1;i<=n;i++) cin>>pre[i].face>>pre[i].na; ans=1; //因为是从第一个人开始的 for(int i=1;i<=m;i++) { cin>>dire>>num; if(pre[ans].face) dire=1-dire; //如果面向圈外就要和面向圈内的方向相反 if(dire==0) { ans-=num; if(ans<=0) ans+=n; //维护环,如果小于等于零就要变成正数 } else { ans+=num; if(ans>n) ans-=n; //维护环,如果超过了就要缩小至人数范围内 } } cout<<pre[ans].na<<endl; return 0; }
