KDtree
What is KDtree?
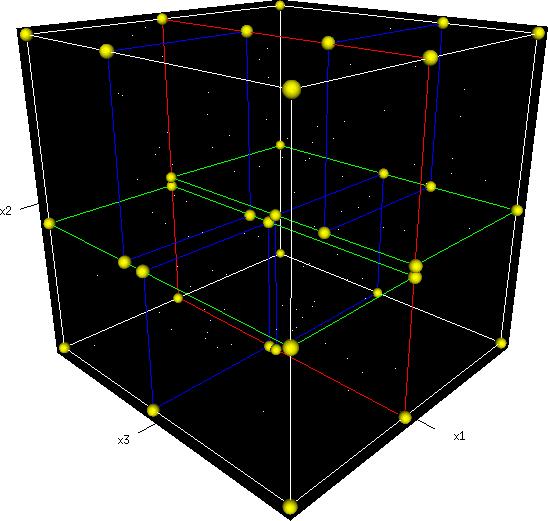
KDtree(K dimensional tree) 是一个支持多维空间的数据结构,主要是将空间内的点进行区域划分,快速维护有关空间点的操作,如空间的最远(近)点对,区间搜索。KDtree的结构与线段树类似,只是线段树是对一维空间的操作,而KDtree是多维操作的,这也导致了KDtree的灵活性没有线段树高。
树上每个点维护的信息:
- 两个儿子
- 该点表示的空间范围(超长方体,2D为矩形,3D为长方体)
- 中位点(坐标等信息)
Operations(Base on 2D)
Build
因为是空间划分,所以要交错地用平行与\\(x, y\\)轴的直线进行划分。
设\\(n\\)个点\\(p_i\\)。
假设现在要用平行于\\(y\\)轴的直线划分区间\\([L, R]\\)(\\(p_i\\)),首先初始化该点的空间范围,然后求出\\([L, R]\\)按\\(x\\)坐标从小到大排序时的中位点,这个可以用nth_element来算,记录中位点(\\(mid\\)),这就将\\([L, R]\\)分成了\\([L, mid-1], [mid+1, R]\\)两部分,然后递归两个区间,而这两个区间要用平行于\\(x\\)轴的直线进行划分,以此类推。
void build(sKDtree *&cur, int L, int R, int type)
//type==0时平行于$y$轴,type==1时平行于$x$轴
{
if (L>R) return;
cur=mem++; //新建一个点
//求空间范围
int le, ri, down, up;
le=down=inf, ri=up=0;
for (int i=L; i<=R; ++i)
{
le=min(le, p[i].x);
ri=max(ri, p[i].x);
down=min(down, p[i].y);
up=max(up, p[i].y);
}
//求中位点
int mid=(L+R)>>1;
if (type) nth_element(p+L, p+mid, p+R+1, cmpy);
else nth_element(p+L, p+mid, p+R+1, cmpx);
//点初始化
cur->init(type, le, ri, down, up);
cur->p=p[mid];
build(cur->son[0], L, mid-1, type^1);
build(cur->son[1], mid+1, R, type^1);
}
ask(以查找欧拉距离最远点为例)
假设要找离\\(p_0\\)欧拉距离最远的点。优先递归答案较优的区间,然后在递归另一个区间,这样剪枝的时候就能减掉更多的区间。例如:假设\\(A\\)是当前的最远点,则灰色区间是不用递归的。我们选择区间的四个角作为区间的代表。

inline int calc_maxdis(sKDtree *cur, Point &p0)
//选择四个角中离p0最远的那个点作为区间的代表
{
if (!cur) return 0;
int ans=sqr(cur->x1-p0.x)+sqr(cur->y1-p0.y);
ans=max(ans, sqr(cur->x1-p0.x)+sqr(cur->y2-p0.y));
ans=max(ans, sqr(cur->x2-p0.x)+sqr(cur->y1-p0.y));
ans=max(ans, sqr(cur->x2-p0.x)+sqr(cur->y2-p0.y));
return ans;
}
void ask(sKDtree *&cur, Point &p0, int &dis)
{
if (!cur) return;
if (calc_maxdis(cur, p0)<=dis) return; //dis是当前最远距离
dis=max(dis, sqr(cur->p.x-p0.x)+sqr(cur->p.y-p0.y));
//判断哪个区间更优
int nid=1;
int d[2];
d[0]=calc_maxdis(cur->son[0], p0);
d[1]=calc_maxdis(cur->son[1], p0);
if (d[0]>d[1]) nid^=1;
//大于当前最优答案的区间进行搜索
if (d[nid]>dis) ask(cur->son[nid], p0, dis);
if (d[nid^1]>dis) ask(cur->son[nid^1], p0, dis);
}
k近邻
\\(k\\)近邻是指找到第\\(k\\)近的点,查找的时候与找最近邻类似,只不过要维护一个大根堆,维护当前\\(k\\)个点中的最远距离,如果当前点比最远距离要小,则更新大根堆,而且利用最远距离可以减掉那些不在当前第\\(k\\)距离内的区间。
注意:由于建树方式的特殊性,使得KDtree难以支持插入操作。
附上模板:Base Stations
#include <bits/stdc++.h>
using namespace std;
const int inf=int(1e9);
const int maxn=int(1e5)+100;
const int maxm=105;
struct base
{
int x, y, type;
bool operator < (const base b) const
{
return type<b.type;
}
};
struct sKDtree
{
sKDtree *son[2];
base p;
int sum[maxm];
int total;
int x1, x2, y1, y2;
int type;
inline void init(int _type=0, int _x1=0, int _x2=0, int _y1=0, int _y2=0)
{
total=0;
for (int i=0; i<maxm; ++i) sum[i]=0;
son[0]=son[1]=NULL;
x1=_x1; y1=_y1; x2=_x2; y2=_y2;
type=_type;
}
void updata()
{
if (son[0])
{
for (int i=0; i<maxm; ++i)
sum[i]+=son[0]->sum[i];
total+=son[0]->total;
}
if (son[1])
{
for (int i=0; i<maxm; ++i)
sum[i]+=son[1]->sum[i];
total+=son[1]->total;
}
}
};
int n;
base station[maxn];
sKDtree memory[maxn*2];
sKDtree *mem=memory;
sKDtree *KDtree;
inline int sqr(int x)
{
return x*x;
}
void read()
{
for (int i=1; i<=n; ++i)
{
base &cur=station[i];
scanf("%d%d%d", &cur.x, &cur.y, &cur.type);
}
}
inline bool cmp0(base &b, base &c)
{
return b.x<c.x;
}
inline bool cmp1(base &b, base &c)
{
return b.y<c.y;
}
void build(sKDtree *&cur, int L, int R, int type)
{
if (L>R) return;
cur=mem++;
int le, ri, down, up;
le=down=inf, ri=up=0;
for (int i=L; i<=R; ++i)
{
base &cur=station[i];
le=min(le, cur.x);
ri=max(ri, cur.x);
down=min(down, cur.y);
up=max(up, cur.y);
}
int mid=(L+R)>>1;
if (type) nth_element(station+L, station+mid, station+R+1, cmp1);
else nth_element(station+L, station+mid, station+R+1, cmp0);
cur->init(type, le, ri, down, up);
cur->p=station[mid];
cur->sum[station[mid].type]++;
cur->total=1;
build(cur->son[0], L, mid-1, type^1);
build(cur->son[1], mid+1, R, type^1);
cur->updata();
if (cur->son[0])
{
for (int i=0; i<maxm; ++i)
cur->sum[i]+=cur->son[0]->sum[i];
cur->total+=cur->son[0]->total;
}
if (cur->son[1])
{
for (int i=0; i<maxm; ++i)
cur->sum[i]+=cur->son[1]->sum[i];
cur->total+=cur->son[1]->total;
}
}
inline int calc_maxdis(sKDtree *cur, base &psta)
{
if (!cur) return 0;
int ans=sqr(cur->x1-psta.x)+sqr(cur->y1-psta.y);
ans=max(ans, sqr(cur->x1-psta.x)+sqr(cur->y2-psta.y));
ans=max(ans, sqr(cur->x2-psta.x)+sqr(cur->y1-psta.y));
ans=max(ans, sqr(cur->x2-psta.x)+sqr(cur->y2-psta.y));
return ans;
}
void ask(sKDtree *&cur, base &psta, int &dis)
{
if (!cur) return;
if (cur->total==cur->sum[psta.type]) return;
if (calc_maxdis(cur, psta)<=dis) return;
if (cur->p.type!=psta.type)
dis=max(dis, sqr(cur->p.x-psta.x)+sqr(cur->p.y-psta.y));
int nid=1;
int d[2];
d[0]=calc_maxdis(cur->son[0], psta);
d[1]=calc_maxdis(cur->son[1], psta);
if (d[0]>d[1]) nid^=1;
if (d[nid]>dis) ask(cur->son[nid], psta, dis);
if (d[nid^1]>dis) ask(cur->son[nid^1], psta, dis);
}
void solve()
{
for (int i=0; i<=n; ++i) (memory+i)->init();
mem=memory;
KDtree=NULL;
int ans=0;
build(KDtree, 1, n, 0);
for (int i=1; i<=n; ++i)
ask(KDtree, station[i], ans);
printf("%d\\n", ans);
}
int main()
{
while(scanf("%d", &n)==1 && n)
{
read();
solve();
}
return 0;
}