NOIP2015 信息传递

Posted 2020-10-29 Neworld2002

Description

有\(n\)个同学（编号为\(1\)到\(n\)）正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象，其中，编号为\(i\)的同学的信息传递对象是编号为\(Ti\)同学。

游戏开始时，每人都只知道自己的生日。之后每一轮中，所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象（注意：可能有人可以从若干人那里获取信息，但是每人只会把信息告诉一个人，即自己的信息传递对象）。当有人从别人口中得知自己的生日时，游戏结束。请问该游戏一共可以进行几轮？

Input

输入共2行。

第1行包含1个正整数\(n\)表示\(n\)个人。

第2行包含n个用空格隔开的正整数\(T1,T2,……,Tn\)其中第\(i\)个整数\(Ti\)示编号为\(i\)的同学的信息传递对象是编号为\(Ti\)的同学，\(Ti≤n\)且\(Ti≠i\)

数据保证游戏一定会结束。

Output

输出共 1 行，包含 1 个整数，表示游戏一共可以进行多少轮。

Sample Input

5
2 4 2 3 1

Sample Output

3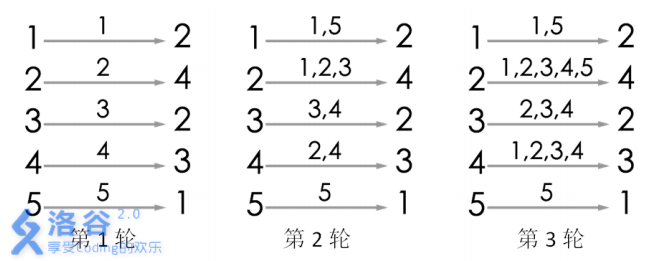

游戏的流程如图所示。当进行完第 3 轮游戏后， 4 号玩家会听到 2 号玩家告诉他自己的生日，所以答案为 3。当然，第 3 轮游戏后， 2 号玩家、 3 号玩家都能从自己的消息来源得知自己的生日，同样符合游戏结束的条件。

对于 30%的数据， n ≤ 200；

对于 60%的数据， n ≤ 2500；

对于 100%的数据， n ≤ 200000。

---

一个找最小环的问题。

暴力+DFS是会超时的。

于是想着来一点优化。

分析：

因为每个人到另一个人只有一条直接相连的边

不难想出每条联通块最多只有一个环！

因为如果有多个环，那么有一个节点必须有多条边，不然无法连到其他节点。

所以如果在某个联通块上找到一个环，那么所有联通块上的节点都不需要DFS了！

#include <cstdio>
#include <cstring>
#define MAXN 200005

int link[MAXN];
int vis[MAXN];
int c[MAXN];
int N;

inline bool dfs(int u,int step){
    
    if(vis[u]==2147483647)return false;
    if(vis[u] != 0){
        c[u] = step - vis[u];
        return true;
    }
    
    vis[u] = step;
    bool flag = dfs(link[u],step+1);
    if(!flag)vis[u] = 0;
    else vis[u] = 2147483647;
    return flag;
}

int main(){
    
    std::memset(vis,0,sizeof(vis));
    std::memset(c,0,sizeof(c));
    
    scanf("%d",&N);
    for(register int i=1;i<=N;++i){
        scanf("%d",&link[i]);
    }
    
    int min = 2147483647;
    
    for(register int i=1;i<=N;++i){
        if(vis[i]==0)dfs(i,1);
    }
    
    for(register int i=1;i<=N;++i){
        if(c[i]!=0&&c[i]<min)min=c[i];
    }
    printf("%d",min);
    return 0;
}