水题（并查集+判断是否是树）(详细测试数据)

Posted 2020-10-29 萧魂不散

A tree is a well-known data structure that is either empty (null, void, nothing) or is a set of one or more nodes connected by directed edges between nodes satisfying the following properties.
There is exactly one node, called the root, to which no directed edges point.

Every node except the root has exactly one edge pointing to it.

There is a unique sequence of directed edges from the root to each node.

For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.



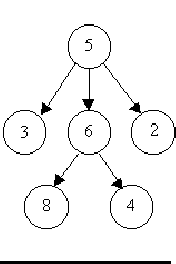
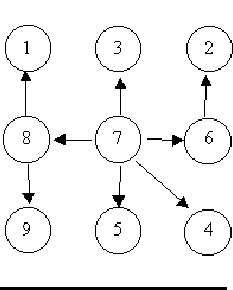
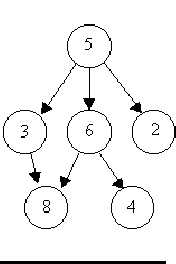
In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.

 

 

Input

The input will consist of a sequence of descriptions (test cases) followed by a pair of negative integers. Each test case will consist of a sequence of edge descriptions followed by a pair of zeroes Each edge description will consist of a pair of integers; the first integer identifies the node from which the edge begins, and the second integer identifies the node to which the edge is directed. Node numbers will always be greater than zero.

 

 

Output

For each test case display the line ``Case k is a tree." or the line ``Case k is not a tree.", where k corresponds to the test case number (they are sequentially numbered starting with 1).

 

 

Sample Input

6 8 5 3 5 2 6 4 5 6 0 0 8 1 7 3 6 2 8 9 7 5 7 4 7 8 7 6 0 0 3 8 6 8 6 4 5 3 5 6 5 2 0 0 -1 -1

 

 

Sample Output

Case 1 is a tree. Case 2 is a tree. Case 3 is not a tree.

 

 

Source

North Central North America 1997 

题意：判断给出的数据是否是一棵树

注意点：

1：空树也是树（0，0）

2：小心成环（1，2，2，1，0，0）

3：只有一个点入度为零（根节点），其他节点入度只能为1（只能有一个根节点，也就是一个集合）

4：是以负数为结束标志

例：

6 8 5 3 5 2 6 4 5 6 0 0

8 1 7 3 6 2 8 9 7 5 7 4 7 8 7 6 0 0

3 8 6 8 6 4 5 3 5 6 5 2 0 0

0 0

1 2 3 4 4 3 0 0

1 2 3 4 0 0

1 2 2 1 0 0

1 1 0 0

2 3 0 0

1 2 2 3 3 1 5 6 0 0

1 2 2 3 3 4 4 1 0 0

yes

yes

no

yes

no

no

no

no

yes

no

no

如果这些数据都对了的话差不多就过了

代码：

#include<stdio.h>
#include<map>
#include<string.h>
#include<queue>
using namespace std;
map<int,int> mp;
queue<int> v;
int lg;
int fz[100050],vt[100050];
int add(int b)
{
　　if(mp.count(b))//记录入度是否超过1
　　lg=0;
　　else
　　mp[b]=1;
　　return 0;
}
int find(int a)
{
　　if(fz[a]==a||fz[a]==-1)
　　return fz[a]=a;//因为一开始fz全赋值为-1，所以在这要赋为它自己
　　return fz[a]=fz[fz[a]];
}
int main()
{
　　int i,j,k;
　　j=0;
　　int a,b;
　　while(scanf("%d%d",&a,&b)!=EOF&&(a>=0||b>=0))
　　{
　　　　lg=1;
　　　　j++;
　　　　k=0;
　　　　mp.clear();//记得清空mp
　　　　memset(fz,-1,sizeof(fz));
　　　　memset(vt,0,sizeof(vt));
　　　　add(b);//计算入度
　　　　if(vt[a]==0)
　　　　v.push(a),vt[a]=1;//记录有哪些点，节省时间
　　　　if(vt[b]==0)
　　　　v.push(b),vt[b]=1;
　　　　int c,d;
　　　　c=find(a);
　　　　d=find(b);
　　　　if(c!=d);//将两个合并为一个集合
　　　　fz[c]=d;
　　　　if(a!=0||b!=0)//判断是否为空树
　　　　while(scanf("%d%d",&a,&b)!=EOF&&(a+b))
　　　　{
　　　　　　if(vt[a]==0)
　　　　　　v.push(a),vt[a]=1;
　　　　　　if(vt[b]==0)
　　　　　　v.push(b),vt[b]=1;
　　　　　　add(b);
　　　　　　int c,d;
　　　　　　c=find(a);
　　　　　　d=find(b);
　　　　　　if(c!=d);
　　　　　　fz[c]=d;
　　　　}
　　　　else
　　　　k=1;
　　　　int sum=0;
　　　　int cnt=0;
　　　　while(!v.empty())
　　　　{
　　　　　　int y=v.front();
　　　　　　v.pop();
　　　　　　//printf("w%d %d\n",y,fz[y]);
　　　　　　if(y==fz[y])
　　　　　　sum++;
　　　　　　if(!mp.count(y))//小心环，例1 2 2 1 0 0，如果没有这条语句则显示是树，而它不是
　　　　　　cnt++;
　　　　}
　　　　//printf("%d %d\n",lg,sum);
　　　　if(k==1)//判断是否是空树
　　　　printf("Case %d is a tree.\n",j);
　　　　else if(lg&&sum==1&&cnt==1)//判断是否是树
　　　　printf("Case %d is a tree.\n",j);
　　　　else
　　　　printf("Case %d is not a tree.\n",j);
　　}
　　return 0;
}