[从头学数学] 第215节 带着计算机去高考

Posted 2020-07-09 mwsister

剧情提要：
[机器小伟]在[工程师阿伟]的陪同下进入了[九转金丹]之第八转的修炼。设想一个场景：
如果允许你带一台不连网的计算机去参加高考，你会放弃选择一个手拿计算器和草稿本吗
？阿伟决定和小伟来尝试一下用计算机算高考题会是怎样的感觉。

正剧开始：

星历2016年05月20日 17:13:35, 银河系厄尔斯星球中华帝国江南行省。
[工程师阿伟]正在和[机器小伟]一起做着2006年的江苏省数学高考题]。

这一年，江苏重新使用了全国卷，并且这张试卷的难度也比较高，可以说，

也是打了考生一个措手不及。因为前两年试题太简单了，各学校又忘了

2003年的滑铁卢之痛了。

不过这次题目的难度前移到客观题部分了，也就说你就算蒙也能蒙点分回来，

后面的大题少了一个，选择题让了两题给填空，大致也就这样了。

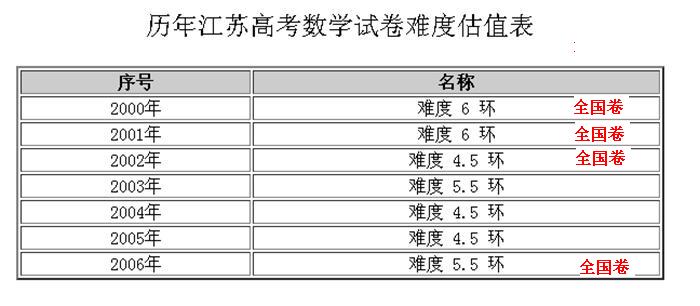
总的来说，主观题难度在五环以下，而选择题、填空题却有非常难的。

其实就拿分的容易度来说，这张卷子比03年卷好拿分多了。

但这里还是给它评以5.5环的难度吧，其实阿伟觉得给5环难度更合适。

<span style="font-size:18px;">//题1
	if (1) {      
        var r = 20;            
        config.setSector(1,1,1,1);              
        config.graphpaper2D(0, 0, r);            
        config.axis2D(0, 0,180);              
                
        //坐标轴设定        
        var scaleX = 2*r, scaleY = 2*r;          
        var spaceX = 2, spaceY = 2;           
        var xS = -10, xE = 10;          
        var yS = -20, yE = 20;          
        config.axisSpacing(xS, xE, spaceX, scaleX, 'X');            
        config.axisSpacing(yS, yE, spaceY, scaleY, 'Y');            
                    
        var transform = new Transform();            
        //存放函数图像上的点        
        var a = [], b = [], c = [], d = [];          
                  
        //需要显示的函数说明    
                    //希腊字母表(存此用于Ctrl C/V  
            //ΑΒΓΔΕΖΗΘΙΚΛΜΝΞΟΠΡΣΤΥΦΧΨΩ  
            //αβγδεζηθικλμνξοπρστυφχψω  
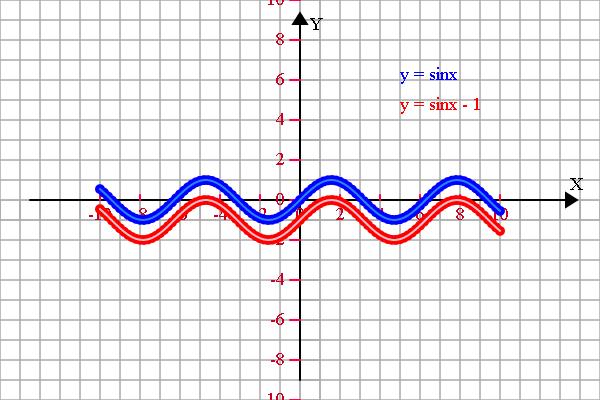
        var f1 = 'y = sinx - 1', f2 = 'y = sinx', f3 = '', f4 = '';        
        var  y1 = y2 = 0;
		//(1-(x+2)^2)^0.5
		for (var x = xS; x <= xE; x+=0.2) { 
				y1 = Math.sin(x)-1;
				y2 = Math.sin(x);
				
				a.push([x, y1]);
				b.push([x, y2]);

        }  
          
                  
        //存放临时数组        
        var tmp = [];        
                  
        //显示变换        
        if (a.length > 0) {        
            a = transform.scale(transform.translate(a, 0, 0), scaleX/spaceX, scaleY/spaceY);         
            //函数1        
            tmp = [].concat(a);            
            shape.pointDraw(tmp, 'red');            
           
			tmp = [].concat(a);            
            shape.multiLineDraw(tmp, 'pink');          
                      
            plot.setFillStyle('red');        
            plot.fillText(f1, 100, -90, 200);          
        }  
		
		        //显示变换        
        if (b.length > 0) {        
            b = transform.scale(transform.translate(b, 0, 0), scaleX/spaceX, scaleY/spaceY);         
            //函数1        
            tmp = [].concat(b);            
            shape.pointDraw(tmp, 'blue');            
           
			tmp = [].concat(b);            
            shape.multiLineDraw(tmp, '#2288FF');          
                      
            plot.setFillStyle('blue');        
            plot.fillText(f2, 100, -120, 200);          
        }  

    } 
	</span>

<span style="font-size:18px;">//题2
	if (1) {      
        var r = 20;            
        config.setSector(1,1,1,1);              
        config.graphPaper2D(0, 0, r);            
        config.axis2D(0, 0,180);              
                
        //坐标轴设定        
        var scaleX = 2*r, scaleY = 2*r;          
        var spaceX = 0.8, spaceY = 0.8;           
        var xS = -10, xE = 10;          
        var yS = -20, yE = 20;          
        config.axisSpacing(xS, xE, spaceX, scaleX, 'X');            
        config.axisSpacing(yS, yE, spaceY, scaleY, 'Y');            
                    
        var transform = new Transform();            
        //存放函数图像上的点        
        var a = [], b = [], c = [], d = [];          
                  
        //需要显示的函数说明    
                    //希腊字母表(存此用于Ctrl C/V  
            //ΑΒΓΔΕΖΗΘΙΚΛΜΝΞΟΠΡΣΤΥΦΧΨΩ  
            //αβγδεζηθικλμνξοπρστυφχψω  
		var f1 = '(x-1)^[2]+(y+1.732)^[2] = 1';
		
		a = shape.nEdge(0, 0, 1, 36);
          
                  
        //存放临时数组        
        var tmp = [];        
                  
        //显示变换        
        if (a.length > 0) {        
            a = transform.scale(transform.translate(a, 1, -1.732), scaleX/spaceX, scaleY/spaceY);         
            //函数1        
            tmp = [].concat(a);            
            shape.pointDraw(tmp, 'red');            
           
			tmp = [].concat(a);            
            shape.multiLineDraw(tmp, 'pink');          
                      
            plot.setFillStyle('red');        
            plot.fillText(f1, 100, -90, 200);          
        }  
	}
		</span>

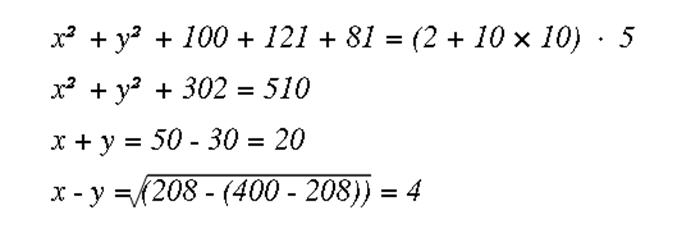
<span style="font-size:18px;">//题3
	if (1) {
		var mathText = new MathText();
		
		//希腊字母表(存此用于Ctrl C/V
			//ΑΒΓΔΕΖΗΘΙΚΛΜΝΞΟΠΡΣΤΥΦΧΨΩ
			//αβγδεζηθικλμνξοπρστυφχψω
		
		
		var s = [
			'x^[2] + y^[2] + 100 + 121 + 81 = (2 + 10*10) * 5',
			'x^[2] + y^[2] + 302 = 510',
			'x + y = 50-30 = 20',
			'|x-y| = (208-(400-208))^[0.5] = 4'
			
			
		];
		
		var x =40, y=40;
		var r1 = 40;
			
		var len = s.length;
		for (var i = 0; i < len; i++) {
		
			if (s[i] == '') {
				if (x < 100) {
					x += 300;
					y-=r1*3;
				}
				else {
					x = 20;
					y += r1;
				}
			}
			else {			
				mathText.print(s[i], x, y, '@');
				y+=r1;
			}
		}		
	
	}</span>

<span style="font-size:18px;">//题4
	if (1) {      
        var r = 20;            
        config.setSector(1,1,1,1);              
        config.graphPaper2D(0, 0, r);            
        config.axis2D(0, 0,180);              
                
        //坐标轴设定        
        var scaleX = 2*r, scaleY = 2*r;          
        var spaceX = 90, spaceY = 1;           
        var xS = -720, xE = 720;          
        var yS = -10, yE = 10;          
        config.axisSpacing(xS, xE, spaceX, scaleX, 'X');            
        config.axisSpacing(yS, yE, spaceY, scaleY, 'Y');            
                    
        var transform = new Transform();            
        //存放函数图像上的点        
        var a = [], b = [], c = [], d = [];          
                  
        //需要显示的函数说明    
                    //希腊字母表(存此用于Ctrl C/V  
            //ΑΒΓΔΕΖΗΘΙΚΛΜΝΞΟΠΡΣΤΥΦΧΨΩ  
            //αβγδεζηθικλμνξοπρστυφχψω  
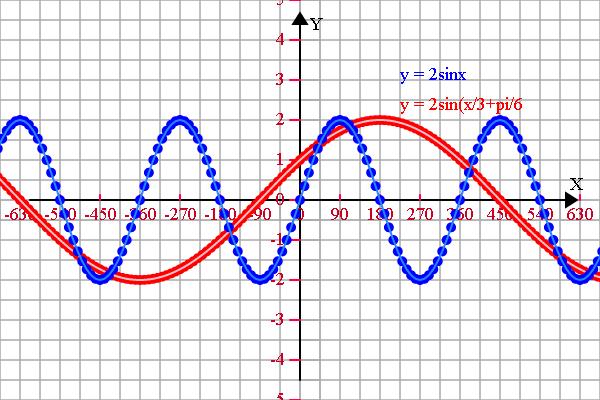
        var f1 = 'y = 2sin(x/3+pi/6)', f2 = 'y = 2sinx', f3 = '', f4 = '';        
        var  y1 = y2 = 0;
		//(1-(x+2)^2)^0.5
		for (var x = xS; x <= xE; x+=10) { 
				y1 = 2*Math.sin(x/3/180*Math.PI+1/6*Math.PI);
				y2 = 2*Math.sin(x/180*Math.PI)
				a.push([x, y1]);
				b.push([x, y2]);

        }  
          
                  
        //存放临时数组        
        var tmp = [];        
                  
        //显示变换        
        if (a.length > 0) {        
            a = transform.scale(transform.translate(a, 0, 0), scaleX/spaceX, scaleY/spaceY);         
            //函数1        
            tmp = [].concat(a);            
            shape.pointDraw(tmp, 'red');            
           
			tmp = [].concat(a);            
            shape.multiLineDraw(tmp, 'pink');        
                      
            plot.setFillStyle('red');        
            plot.fillText(f1, 100, -90, 200);          
        }  
		
		//显示变换        
        if (b.length > 0) {        
            b = transform.scale(transform.translate(b, 0, 0), scaleX/spaceX, scaleY/spaceY);         
            //函数1        
            tmp = [].concat(b);            
            shape.pointDraw(tmp, 'blue');            
           
			tmp = [].concat(b);            
            shape.multiLineDraw(tmp, '#2288FF');          
                      
            plot.setFillStyle('blue');        
            plot.fillText(f2, 100, -120, 200);          
        }  

    } 
	</span>

<span style="font-size:18px;">#题5
def tmp5():
    a = alg.strformat(['x^[0.5]', '(1/3)*x^[-1]']);

    a = alg.strpow_n(a, 10);
    a = alg.strcombine(a);
    print(a);
	
>>> 
['(1)*x^[5.0]', '(3.33333)*x^[3.5]', '(4.999995)*x^[2.0]', '(4.44444)*x^[0.5]', 
'(2.59266)*x^[-1.0]', '(1.03698)*x^[-2.5]', '(0.28812)*x^[-4.0]', '(0.05484)*x^[-5.5]', 
'(0.00684)*x^[-7.0]', '(0.00051)*x^[-8.5]', '(1.7e-05)*x^[-10]']
</span>

<span style="font-size:18px;">#题6
def tmp6():
    P = ['x', 'y'];
    abs_MN = 4;
    abs_MP_2 = ['x^[2]', '4x', '4', 'y^[2]']; #'((x+2)^[2]+y^[2])^[0.5]';
    
    MN = ['4x', '-8'] #'(4, 0)*(x-2, y) = 4x-8

    abs_MP_2 = alg.strformat(abs_MP_2);
    MN = alg.strformat(MN);

    MN_2 = alg.strpow_n(MN, 2);
    MN_2 = alg.strcombine(MN_2);

    MN_2 = alg.minus(MN_2);

    abs_MP_2 = alg.strdot(abs_MP_2, ['16']);
    result = alg.stradd(abs_MP_2 , MN_2);
    result = alg.strcombine(result);
    print(result);

#这个多项式 = 0
>>> 
['(0)', '(128)*x^[1]', '(0)', '(16)*y^[2]']</span>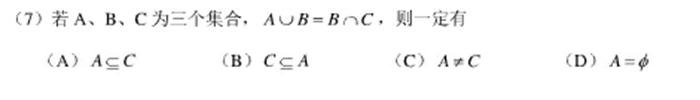

<span style="font-size:18px;">#题8
def tmp8():
    num = [1, 2, 3];

    answer = 'ABCD';

    for i in range(3):
        a = num[(i)%3];
        b = num[(i+1)%3];
        c = num[(i+2)%3];

        if (abs(a-b) <= abs(a-c)+abs(b-c)):
            print('A');

        if (a**2+1/(a**2) >= a + 1/a):
            print('B');

        if (abs(a-b) + 1/(a-b) >= 2):
            print('C');

        if (math.sqrt(a+3) - math.sqrt(a+1) <= math.sqrt(a+2) - math.sqrt(a)):
            print('D');

        print('----');
		
>>> 
A
B
D
----
A
B
D
----
A
B
C
D
----
</span>

<span style="font-size:18px;">#题10
def tmp10():
	#下面是错误的解答，但是知道哪些思考是错的也重要
	
    #只要所有线路的开头和结尾的序号都不一样，就可以全部连通

    #总连接数
    total = (alg.arrangement(6, 6))**2;
    print(total);

    #目标连接数
    #源
    t_0 = 6*5;
    t_1 = 5*4;
    t_2 = 4*3;
    t_3 = 3*2;
    t_4 = 2*1;

    choice = t_0*t_1*t_2*t_3*t_4;
    print(choice/total); #1/6

    #现在分成三组，左边先任意分，不用管
    #右边要保证任意一组都不能两个头和左边完全一样，
    #至少要有一个不一样

    #0个位置相同
    p_0 = alg.arrangement(5, 5);
    #6个位置只有一个相同
    p_1 = 6 * alg.arrangement(4, 4);
    #6个位置有两个相同，但不能在一组
    p_2 = alg.combination(3, 2)*alg.arrangement(3, 3);
    #有3个相同
    p_3 = alg.arrangement(2, 2);

    res = (p_0+p_1+p_2+p_3)
    total = alg.arrangement(6, 6);
    print(res);
    print(res/total);
	
	#正确答案是8/15，让人吐血的题</span>

<span style="font-size:18px;">#题12
def tmp12():
    BC = 12;
    A = 60;
    B = 45;
    
    tri_ABC = geo.solveTriangle([BC, '?', '?', A, B, '?']);

    AC = tri_ABC[1];
    print(AC);
	
>>> 
9.797958971132712</span>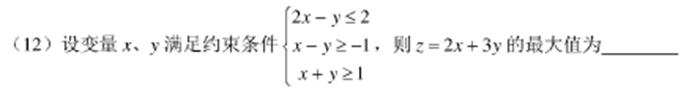

<span style="font-size:18px;">#题13
def tmp13():
    total = alg.arrangement(9, 9);
    red = alg.arrangement(2,2);
    yellow = alg.arrangement(3, 3);
    white = alg.arrangement(4, 4);

    total /= (red*yellow*white);
    print(total);
	
>>> 
1260.0</span>

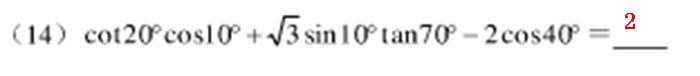
<span style="font-size:18px;">#题14
def tmp14():
    a = 70/180*math.pi;
    b = 10/180*math.pi;
    c = 40/180*math.pi;
    
    result = math.tan(a)*math.cos(b)+1.732*math.sin(b)*math.tan(a)-2*math.cos(c);
    print(result);</span>

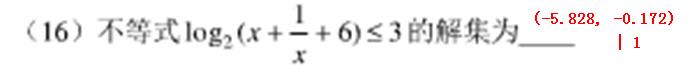
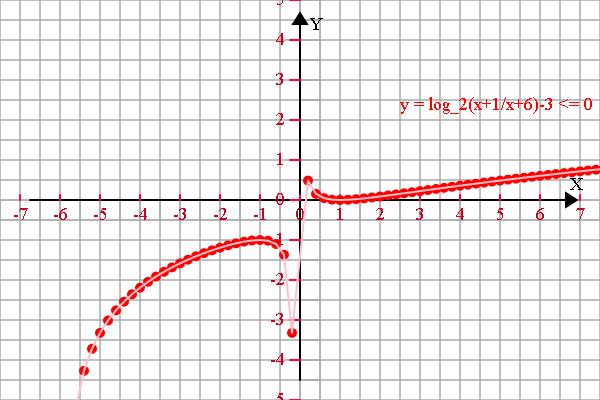
这个题有定义域的问题。

<span style="font-size:18px;">//题17
	if (1) {      
        var r = 20;            
        config.setSector(1,1,1,1);              
        config.graphPaper2D(0, 0, r);            
        config.axis2D(0, 0,180);              
                
        //坐标轴设定        
        var scaleX = 2*r, scaleY = 2*r;          
        var spaceX = 1, spaceY = 5;           
        var xS = -10, xE = 10;          
        var yS = -20, yE = 20;          
        config.axisSpacing(xS, xE, spaceX, scaleX, 'X');            
        config.axisSpacing(yS, yE, spaceY, scaleY, 'Y');            
                    
        var transform = new Transform();            
        //存放函数图像上的点        
        var a = [], b = [], c = [], d = [];          
                  
        //需要显示的函数说明    
                    //希腊字母表(存此用于Ctrl C/V  
            //ΑΒΓΔΕΖΗΘΙΚΛΜΝΞΟΠΡΣΤΥΦΧΨΩ  
            //αβγδεζηθικλμνξοπρστυφχψω  
        var f1 = 'y = log_2(x+1/x+6)-3 <= 0', f2 = '', f3 = '', f4 = '';        
        var  y1 = y2 = 0;
		//(1-(x+2)^2)^0.5
		for (var x = xS; x <= xE; x+=0.2) { 
				y1 = Math.log(x+1/x+6)/Math.log(2) - 3;
				
				a.push([x, y1]);


        }  
          
                  
        //存放临时数组        
        var tmp = [];        
                  
        //显示变换        
        if (a.length > 0) {        
            a = transform.scale(transform.translate(a, 0, 0), scaleX/spaceX, scaleY/spaceY);         
            //函数1        
            tmp = [].concat(a);            
            shape.pointDraw(tmp, 'red');            
           
			tmp = [].concat(a);            
            shape.multiLineDraw(tmp, 'pink');          
                      
            plot.setFillStyle('red');        
            plot.fillText(f1, 100, -90, 200);          
        }  
		
		        //显示变换        
        if (b.length > 0) {        
            b = transform.scale(transform.translate(b, 0, 0), scaleX/spaceX, scaleY/spaceY);         
            //函数1        
            tmp = [].concat(b);            
            shape.pointDraw(tmp, 'blue');            
           
			tmp = [].concat(b);            
            shape.multiLineDraw(tmp, '#2288FF');          
                      
            plot.setFillStyle('blue');        
            plot.fillText(f2, 100, -120, 200);          
        }  

    } </span>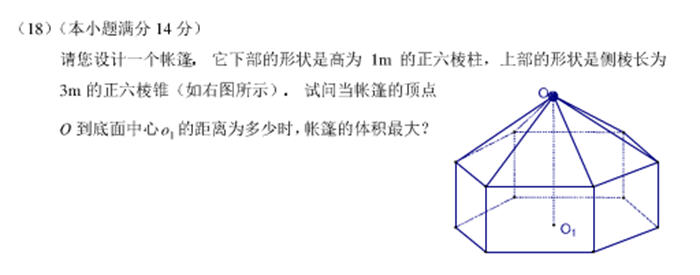

<span style="font-size:18px;">#题19
def tmp19():
    AB = AC = BC = 3;
    AE = CP = CF = 1;
    AF = BE = BP = 2;

    A = B = C = 60;

    A1E = AE;

    #设ED 是过E垂直于BP
    DE = 3*1.732/2*2/3;

    #解三角形A1DE
    tri_A1DE = geo.solveTriangle([DE, A1E, '?', '?', '?', 90]);
    #直线A1E与平面A1BP所成的角
    angle = tri_A1DE[3];
    print(angle);
	
>>> 
59.999272219172646
</span>

本节到此结束，欲知后事如何，请看下回分解。