[从头学数学] 第214节 带着计算机去高考

Posted 2020-07-09 mwsister

剧情提要：
[机器小伟]在[工程师阿伟]的陪同下进入了[九转金丹]之第八转的修炼。设想一个场景：
如果允许你带一台不连网的计算机去参加高考，你会放弃选择一个手拿计算器和草稿本吗
？阿伟决定和小伟来尝试一下用计算机算高考题会是怎样的感觉。

正剧开始：

星历2016年05月20日 11:40:58, 银河系厄尔斯星球中华帝国江南行省。
[工程师阿伟]正在和[机器小伟]一起做着2005年的江苏省数学高考题]。

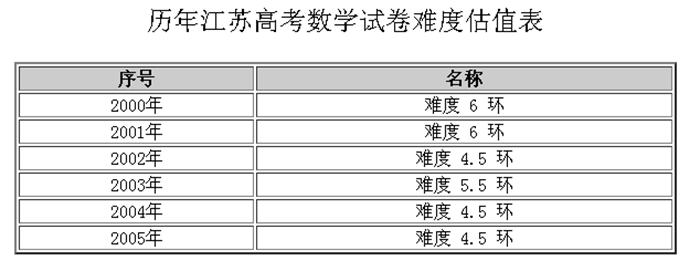
总体来说，这次的难度和上一年持平，都是很厚道的那种，

不过上一年的好多题都像闹着玩似的，这次稍微好点，不过运算量也很小。

然后最大的改变就是打破了持续N年的22题格局，用减少一个主观题为代价，添加了两个填空题。

<span style="font-size:18px;">def tmp1():
    A = set([1, 2]);
    B = set([1,2,3]);
    C = set([2,3,4]);

    D = (A.intersection(B)).union(C);
    print(D);

    E = (A & B) | C;
    print(E);
	
>>> 
{1, 2, 3, 4}
{1, 2, 3, 4}</span>

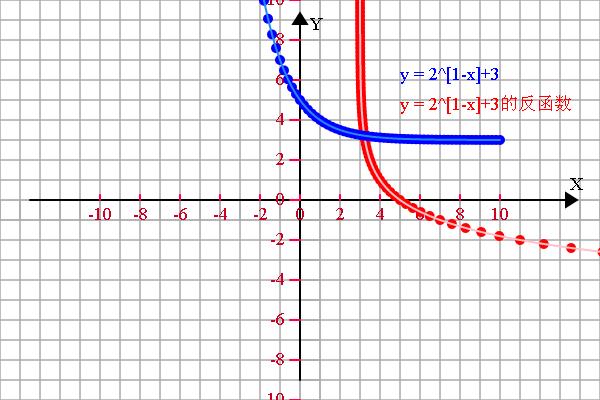
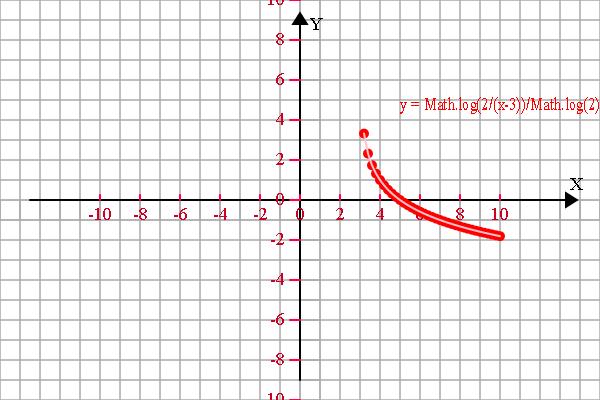
<span style="font-size:18px;">//题2
	if (1) {      
        var r = 20;            
        config.setSector(1,1,1,1);              
        config.graphpaper2D(0, 0, r);            
        config.axis2D(0, 0,180);              
                
        //坐标轴设定        
        var scaleX = 2*r, scaleY = 2*r;          
        var spaceX = 2, spaceY = 2;           
        var xS = -10, xE = 10;          
        var yS = -20, yE = 20;          
        config.axisSpacing(xS, xE, spaceX, scaleX, 'X');            
        config.axisSpacing(yS, yE, spaceY, scaleY, 'Y');            
                    
        var transform = new Transform();            
        //存放函数图像上的点        
        var a = [], b = [], c = [], d = [];          
                  
        //需要显示的函数说明    
                    //希腊字母表(存此用于Ctrl C/V  
            //ΑΒΓΔΕΖΗΘΙΚΛΜΝΞΟΠΡΣΤΥΦΧΨΩ  
            //αβγδεζηθικλμνξοπρστυφχψω  
        var f1 = 'y = 2^[1-x]+3的反函数', f2 = 'y = 2^[1-x]+3', f3 = '', f4 = '';        
        var  y1 = y2 = 0;
		//(1-(x+2)^2)^0.5
		for (var x = xS; x <= xE; x+=0.2) { 
				y1 = Math.pow(2, 1-x)+3;
				a.push([y1, x]);	
				b.push([x, y1]);

        }  
          
                  
        //存放临时数组        
        var tmp = [];        
                  
        //显示变换        
        if (a.length > 0) {        
            a = transform.scale(transform.translate(a, 0, 0), scaleX/spaceX, scaleY/spaceY);         
            //函数1        
            tmp = [].concat(a);            
            shape.pointDraw(tmp, 'red');            
           
			tmp = [].concat(a);            
            shape.multiLineDraw(tmp, 'pink');          
                      
            plot.setFillStyle('red');        
            plot.fillText(f1, 100, -90, 200);          
        }  
		
		        //显示变换        
        if (b.length > 0) {        
            b = transform.scale(transform.translate(b, 0, 0), scaleX/spaceX, scaleY/spaceY);         
            //函数1        
            tmp = [].concat(b);            
            shape.pointDraw(tmp, 'blue');            
           
			tmp = [].concat(b);            
            shape.multiLineDraw(tmp, '#2288FF');          
                      
            plot.setFillStyle('blue');        
            plot.fillText(f2, 100, -120, 200);          
        }  

    } 
	

        var f1 = 'y = Math.log(2/(x-3))/Math.log(2)', f2 = 'y = 2^[1-x]+3', f3 = '', f4 = '';        
        var  y1 = y2 = 0;
		//(1-(x+2)^2)^0.5
		for (var x = xS; x <= xE; x+=0.2) { 
				y1 = Math.log(2/(x-3))/Math.log(2)
				a.push([x, y1]);

        }  </span>

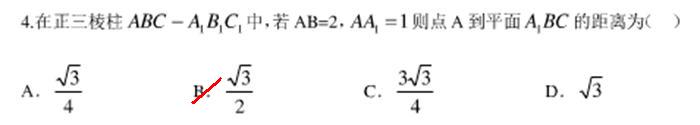
<span style="font-size:18px;">#题4
def tmp4():
    panel = Panel();

    #正三棱柱ABC-A1B1C1
    A, B, C = [0, 0, 0], [2,0,0], [1, 3**0.5, 0];
    A1, B1, C1 = [0, 0, 1], [2,0,1], [1, 3**0.5, 1];

    #平面ABC的法向量
    norm_ABC = panel.normal([A, B, C]);
    print(norm_ABC);

    #平面ABC的一般式方程
    genre_ABC = panel.genreForm([A, B, C]);
    print(genre_ABC);

    #占A到平面A1BC的距离
    dis_A_A1BC = panel.pt2panel(A, [A1, B, C]);
    print(dis_A_A1BC);

>>> 
[0.0, 0, 3.4641016151377544]
[0.0, 0, 3.4641016151377544, -0.0]
0.8660254037844386


###
# @usage   平面解析几何里的平面类，包含相关的一组计算方法
# @author  mw
# @date    2016年05月20日  星期五  09:02:31 
# @param
# @return
#
###

#涉及到平面，所有的坐标点都是空间坐标系[x, y, z]形式
class Panel():
    #平面的法向量， 由[P_[1], P_[2], P_[3]]唯一确定平面
    def normal(self, plain):
        #平面上的三个点
        point_1, point_2, point_3 = plain[0], plain[1], plain[2];
        x_1, y_1, z_1 = point_1[0], point_1[1], point_1[2];
        x_2, y_2, z_2 = point_2[0], point_2[1], point_2[2];
        x_3, y_3, z_3 = point_3[0], point_3[1], point_3[2];

        #中间变量
        a = (y_2-y_1)*(z_3-z_1) - (y_3-y_1)*(z_2-z_1);
        b = (z_2-z_1)*(x_3-x_1) - (z_3-z_1)*(x_2-x_1);
        c = (x_2-x_1)*(y_3-y_1) - (x_3-x_1)*(y_2-y_1);

        return [a, b, c];

    #平面一般式方程，由三个平面点得到Ax+By+Cz+D=0中的四个参数A,B,C,D
    def genreForm(self, plain):
        norm = self.normal(plain);
        a, b, c = norm[0], norm[1], norm[2];

        #平面上的三个点
        point_1, point_2, point_3 = plain[0], plain[1], plain[2];
        x_1, y_1, z_1 = point_1[0], point_1[1], point_1[2];
        x_2, y_2, z_2 = point_2[0], point_2[1], point_2[2];
        x_3, y_3, z_3 = point_3[0], point_3[1], point_3[2];
                                  
        d = -(a*x_1+b*y_1+c*z_1);

        return [a, b, c, d];

    #点到平面的距离
    def pt2panel(self, point, panel):
        #平面一般式的参数
        a, b, c, d = self.genreForm(panel);

        x, y, z = point[0], point[1], point[2];
        distance = abs((a*x+b*y+c*z+d)/(a**2+b**2+c**2)**0.5);

        return distance;
		</span>

<span style="font-size:18px;">#题5
def tmp5():
    #三角形ABC， 多给一条边试算
    tri_ABC = geo.solveTriangle([3, 2, '?', 60, '?', '?']);
    print(tri_ABC);

    BC, AC, AB = tri_ABC[0], tri_ABC[1], tri_ABC[2];
    #周长
    perimeter = BC+AC+AB;
    print(perimeter);

    #角B，转为弧度
    B = tri_ABC[4]/180*math.pi;

    #选项，用于对比
    choice = [4*1.732*math.sin(B+math.pi/3)+3,
              4*1.732*math.sin(B+math.pi/6)+3,
              6*math.sin(B+math.pi/3)+3,
              6*math.sin(B+math.pi/6)+3
              ];
    answer = 'ABCD';
    for i in range(4):
        if abs(choice[i]- perimeter)< 1e-6:
            print(answer[i]);

			
>>> 
[3, 2, 3.4494897427831783, 60.0, 35.264389682754654, 84.73561031724536]
8.449489742783179
D
</span>

<span style="font-size:18px;">//题7
	if (1) {
		analyze = new DataAnalyze();
		
		a = [9.4, 9.4, 9.4, 9.6, 9.7];
		
		hint(analyze.average(a));
		hint(analyze.variance(a));
	
	}

9.5
0.015999999999999886

#题7
def tmp7():
    analyze = DataAnalyze();
    
    array = [9.4, 8.4, 9.4, 9.9, 9.6, 9.4, 9.7];
    array = sorted(array);
    array = array[1:-1];

    print(array);
    array = analyze.format(array);
    sum_ = analyze.sum(array);
    print(sum_);

    aver_ = analyze.average(array);
    print('均值 ', aver_);

    variance = analyze.variance(array);
    print('方差 ', variance);

    #numpy数组的属性
    print(array.ndim);
    print(array.shape);
    print(array.size);
    print(array.dtype);
    print(array.itemsize);
    print(array.data);
	

>>> 
[9.4, 9.4, 9.4, 9.6, 9.7]
47.5
均值  9.5
方差  0.016
1
(5,)
5
float64
8
<memory at 0x0205AD50>

###
# @usage   数据的集中分析类
# @author  mw
# @date    2016年05月20日  星期五  10:06:47 
# @param
# @return
#
###

class DataAnalyze():
    #由于numpy的方法接口只对narray开放，所以，数组先要格式化一下
    #对于自己的数组而言，这个方法是必须要先调用一下，才能使用numpy方法的
    def format(self, array):
        return numpy.array(array);
    
    #求和
    def sum(self, array):        
        return array.sum();

    #均值
    def average(self, array):
        return self.sum(array)/len(array);
        
    #方差
    def variance(self, array):
        array_ = array*array;
        sum_ = array_.sum();
        aver_ = self.average(array);

        result = sum_/len(array) - aver_**2;
        return result;
    
    #标准差
    def RMS(self, array):
        return (self.variance)**0.5;
</span>

<span style="font-size:18px;">#题9
def tmp9():
    a = ['x', '2'];
    a = alg.strformat(a);

    a = alg.strpow_n(a, 5);
    a = alg.strcombine(a);

    print(a);
	
>>> 
['(1)*x^[5]', '(10)*x^[4]', '(40)*x^[3]', '(80)*x^[2]', '(80)*x^[1]', '(32)']</span>

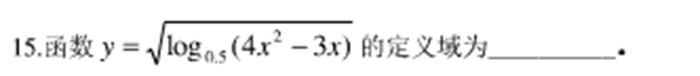
<span style="font-size:18px;">#题16
def tmp16():
    print(math.log(0.618)/math.log(3));</span>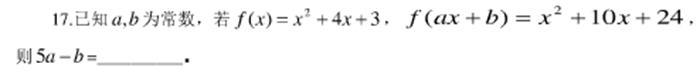

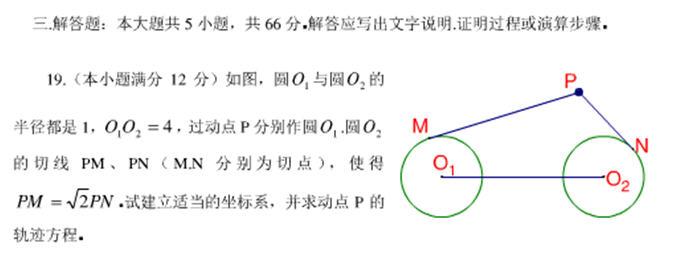
<span style="font-size:18px;">#题20
def tmp20():
    #甲、乙命中率
    p_1 = 2/3;
    p_2 = 3/4;

    #(1)
    print(1-p_1**4);

    #(2) 有组合数相乘
    a = alg.combination(4, 2)*p_1**2*(1-p_1)**2;
    b = alg.combination(4, 3)*p_2**3*(1-p_2);
    print(a*b);

    #(3)
    a12 = 1-(1-p_2)**2; #前两次，只要不是都不击中
    a3 = p_2; #第三次， 必须击中
    a45 = (1-p_2)**2; #第四五次，必须不中
    print(a12*a3*a45);

>>> 
0.8024691358024691
0.12500000000000003
0.0439453125</span>

<span style="font-size:18px;">#题21
def tmp21():
    #已知边
    AS = AB = AE = 2;
    BC = DE = 1.732;

    #已知角
    A = C = D = 120;

    #解三角形，数组是以对边对角的方式排列的
    tri_ABS = geo.solveTriangle(['?', AS, AB, 90, '?', '?']);
    BS = tri_ABS[0];
    ES = BS;

    tri_ABE = geo.solveTriangle(['?', AE, AB, A, '?', '?']);
    BE = tri_ABE[0];

    tri_BES = geo.solveTriangle([ES, BS, BE, '?', '?', '?']);
    print('CD与AB成的角：', tri_BES[3]);
	
>>> 
CD与AB成的角： 52.23875609296496
>>> math.acos(6**0.5/4)*180/3.142
52.23198356916861
>>> math.acos(6**0.5/4)*180/math.pi
52.23875609296496

    #(2)

    #角B
    B = (540-A-C-D)/2;

    #tri_BCD = geo.solveTriangle([CD, '?', BC, '?', C, '?']);
    print(B);

    '''
    >>> 
    CD与AB成的角： 52.23875609296496
    90.0
    '''


</span>

本节到此结束，欲知后事如何，请看下回分解。