网络流
网络流是省选必备算法啊……早就想学了但一直没空……现在学习一下顺便做做笔记
(PS:STO%%%手搓网络流的bGary大佬)
网址整理:
http://blog.csdn.net/ruoruo_cheng/article/details/51815257 网络流常见模型☆
https://www.cnblogs.com/gengchen/p/6605548.html 网络流24题模型分析
https://baike.baidu.com/item/网络流 网络流百度百科
注:本博客可能使用了其他博客的图或者部分内容,若有未标明的麻烦告诉我一声,谢谢
什么是网络流?
图论中的一种理论与方法,研究网络上的一类最优化问题 。
很多系统中涉及流量问题,例如公路系统中车流量,网络中的数据信息流,供油管道的油流量等。我们可以将有向图进一步理解为“流网络”(flow
network),并利用这样的抽象模型求解有关流量的问题。
……
看不懂啊喂
算了还是举栗子好用
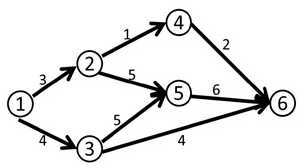
可以类比水流,从1点注水,从6点接收水。每条路即为一个管道,该管道有一定容量(那我们注入的水肯定不能超过这个容量)。求最大的接水量.。
源点:只出不进的点,即上图1点
汇点:只进不出的点,即上图6点
容量:最大承受的量,即上图的边的边权
流量:实际上流过的量。
最小割:从图上拆掉几个边,使源点和汇点不连通的最小花费
(最大流=最小割)
网络流之最大流
一、EK算法(必须理解)
(n*m^2)
求解思路:
首先引入一个概念:可行流。即为各边上的流量都没超过容量的流。
最简单的例子:零流。这个一定是一个可行流。
那么我们就从零流考虑如何找最大流。
(1) 假如有一条源点到汇点的路,路径上的流量都严格小于容量
(2) 那么我们就可以给这条路径增加流量。增加的量delta为各边(容量-流量)中的最小值。
(3) 这样我们就可以找到一个更大的流了。而在(2)中的那条路,就叫做增广路。简单理解就是流量可以在原先基础上增加的路径
(4) 找不到增广路时,当前的流量就是最大流。
那么问题来了:上面的方法并不是完全正确的(?)比如下面的网络流模型:
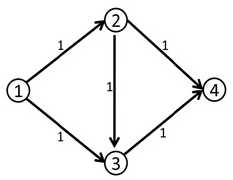
第一次找增广路后就成了下图
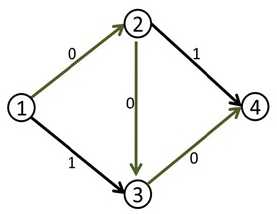
这样的话找一次就没有增广路了,求得最大流为1。
但这显然是错的。因为走(1-2-4)和(1-3-4)才是正确答案,最大流为2.
很显然,我们第一次找增广路的时候将最优的走法堵上了,所以无法求得最优解。
为了解决这个问题,网络流就有一个特别巧妙的方法解决这个问题:反向边
反向边,顾名思义,就是在原有的每条边上建一条方向相反的边,初始值为0。
我们用c[x][y]存x点到y点的容量。每一次找到增广路后,我们在路径上每一条边的容量减少delta的同时,给每条反向边加上delta。
C[x][y]+=delta
C[y][x]-=delta
那上面的例子就可以正确求解了。
一开始找到(1-2-3-4)这条增广路,修改成如下图
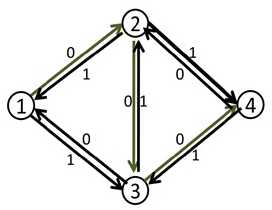
然后再找(1-3-2-4)这条增广路,修改成下图,即可得到最大流2
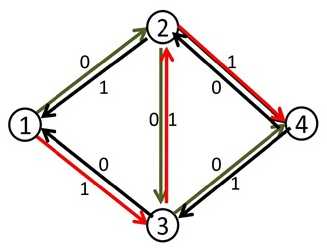
简单理解就是第二次找增广路的时候我们将正向边(2-3)的流量利用反向边“退”了回去。
代码实现:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #include<queue> 6 #define INF (0x7fffffff) 7 #define MAXN (10000+10) 8 #define MAXM (100000+10) 9 using namespace std; 10 bool visit[MAXN]; 11 int pre[MAXN]; 12 int n,m,s,t,Ans; 13 int num_edge,head[MAXN]; 14 int q[MAXN]; 15 struct node 16 { 17 int to; 18 int next; 19 int Flow;//残留网络 20 }edge[MAXM*2]; 21 22 void add(int u,int v,int l) 23 { 24 edge[++num_edge].to=v; 25 edge[num_edge].next=head[u]; 26 edge[num_edge].Flow=l; 27 head[u]=num_edge; 28 } 29 30 bool Bfs(int s,int t) 31 { 32 int Head=0,Tail=1; 33 memset(pre,-1,sizeof(pre)); 34 memset(visit,false,sizeof(visit)); 35 visit[s]=true; 36 q[1]=s; 37 while (Head<Tail) 38 { 39 ++Head; 40 int x=q[Head]; 41 for (int i=head[x];i!=0;i=edge[i].next) 42 if (edge[i].Flow>0 && !visit[edge[i].to]) 43 { 44 pre[edge[i].to]=i; 45 visit[edge[i].to]=true; 46 if (edge[i].to==t) return true; 47 q[++Tail]=edge[i].to; 48 } 49 } 50 return false; 51 } 52 53 int EK(int s,int t) 54 { 55 while (Bfs(s,t)) 56 { 57 int d=INF; 58 for (int i=t;i!=s;i=edge[((pre[i]-1)^1)+1].to) 59 d=min(d,edge[pre[i]].Flow); 60 for (int i=t;i!=s;i=edge[((pre[i]-1)^1)+1].to) 61 { 62 edge[pre[i]].Flow-=d; 63 edge[((pre[i]-1)^1)+1].Flow+=d; 64 } 65 Ans+=d; 66 } 67 return Ans; 68 } 69 70 int main() 71 { 72 int u,v,l; 73 scanf("%d%d%d%d",&n,&m,&s,&t); 74 for (int i=1;i<=m;++i) 75 { 76 77 scanf("%d%d%d",&u,&v,&l); 78 add(u,v,l); 79 add(v,u,0); 80 } 81 printf("%d",EK(s,t)); 82 }
二、Dinic算法
(n^2*m)
求解思路:
只要理解EK,Dinic就很好理解了。在EK中,每找一条增广路就要BFS一次,然后重新BFS,这样的时间复杂度肯定是很大的。这里我们用一个技巧来优化:分层图
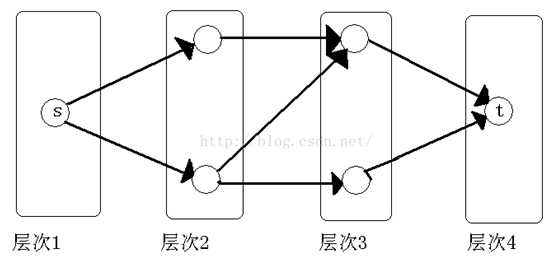
每个点的层次即为其到源点的最短距离,BFS实现。
每次我们BFS构建分层图。如果BFS后发现有增广路,那么我们DFS在这个分层图上找所有可行增广路(多路增广)。
注意:DFS时只能往比自己深1的点走。
代码实现:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #define MAXM (100000+10) 6 #define MAXN (10000+10) 7 using namespace std; 8 struct node 9 { 10 int Flow; 11 int next; 12 int to; 13 } edge[MAXM*2]; 14 int Depth[MAXN],q[MAXN]; 15 int head[MAXN],num_edge; 16 int n,m,s,e; 17 18 void add(int u,int v,int l) 19 { 20 edge[++num_edge].to=v; 21 edge[num_edge].Flow=l; 22 edge[num_edge].next=head[u]; 23 head[u]=num_edge; 24 } 25 26 bool Bfs(int s,int e) 27 { 28 int Head=0,Tail=1; 29 memset(Depth,0,sizeof(Depth)); 30 Depth[s]=1; 31 q[1]=s; 32 while (Head<Tail) 33 { 34 ++Head; 35 int x=q[Head]; 36 for (int i=head[x]; i!=0; i=edge[i].next) 37 if (!Depth[edge[i].to] && edge[i].Flow>0) 38 { 39 Depth[edge[i].to]=Depth[x]+1; 40 q[++Tail]=edge[i].to; 41 } 42 } 43 if (Depth[e]>0) return true; 44 return false; 45 } 46 47 int Dfs(int x,int low) 48 { 49 int Min,f=0; 50 if (x==e || low==0) 51 return low; 52 for (int i=head[x]; i!=0; i=edge[i].next) 53 if (edge[i].Flow>0 && Depth[edge[i].to]==Depth[x]+1 && (Min=Dfs(edge[i].to , min(low,edge[i].Flow) ))) 54 { 55 edge[i].Flow-=Min; 56 edge[((i-1)^1)+1].Flow+=Min; 57 f+=Min; 58 low-=Min; 59 } 60 return f; 61 } 62 63 int Dinic(int s,int e) 64 { 65 int Ans=0,Road; 66 while (Bfs(s,e)) 67 Ans+=Dfs(s,0x7fffffff); 68 return Ans; 69 } 70 71 int main() 72 { 73 int u,v,l; 74 scanf("%d%d%d%d",&n,&m,&s,&e); 75 for (int i=1; i<=m; ++i) 76 { 77 scanf("%d%d%d",&u,&v,&l); 78 add(u,v,l); 79 add(v,u,0); 80 } 81 printf("%d",Dinic(s,e)); 82 }
网络流之费用流
一、 EK+SPFA
恩……这个还是需要EK+贪心的思想。
每次找一个最小花费的增广路,然后增广。可以证明当前费用为达到当前流量的最小花费。
至于找最小花费的增广路,用SPFA替换EK里的BFS就可以了。
注意:建边时反向边的花费要设置成正向边的相反数。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #define MAXN (5000+10) 5 #define MAXM (50000+10) 6 using namespace std; 7 int pre[MAXN],n,m,s,e,Ans,num_edge,head[MAXN],q[MAXN*100]; 8 int dis[MAXN],INF,u,v,l,c; 9 bool used[MAXN]; 10 struct node 11 { 12 int to; 13 int next; 14 int Flow;//残留网络 15 int Cost; 16 } edge[MAXM*2]; 17 18 void add(int u,int v,int l,int c) 19 { 20 edge[++num_edge].to=v; 21 edge[num_edge].next=head[u]; 22 edge[num_edge].Flow=l; 23 edge[num_edge].Cost=c; 24 head[u]=num_edge; 25 } 26 27 bool Spfa(int s,int e) 28 { 29 int Head=0,Tail=1; 30 memset(pre,-1,sizeof(pre)); 31 memset(dis,0x7f,sizeof(dis)); 32 q[1]=s; 33 dis[s]=0; 34 used[s]=true; 35 while (Head<Tail) 36 { 37 int x=q[++Head]; 38 for (int i=head[x]; i!=0; i=edge[i].next) 39 if (dis[x]+edge[i].Cost<dis[edge[i].to] && edge[i].Flow>0) 40 { 41 dis[edge[i].to]=edge[i].Cost+dis[x]; 42 pre[edge[i].to]=i; 43 if (!used[edge[i].to]) 44 { 45 used[edge[i].to]=true; 46 q[++Tail]=edge[i].to; 47 } 48 } 49 used[x]=false; 50 } 51 return (dis[e]!=INF); 52 } 53 54 void MCMF(int s,int e) 55 { 56 int Ans=0,Fee=0; 57 while (Spfa(s,e)) 58 { 59 int d=INF; 60 for (int i=e; i!=s; i=edge[((pre[i]-1)^1)+1].to) 61 d=min(d,edge[pre[i]].Flow); 62 for (int i=e; i!=s; i=edge[((pre[i]-1)^1)+1].to) 63 { 64 edge[pre[i]].Flow-=d; 65 edge[((pre[i]-1)^1)+1].Flow+=d; 66 } 67 Ans+=d; 68 Fee+=d*dis[e]; 69 } 70 printf("%d %d",Ans,Fee); 71 } 72 int main() 73 { 74 memset(&INF,0x7f,sizeof(INF)); 75 scanf("%d%d%d%d",&n,&m,&s,&e); 76 for (int i=1; i<=m; ++i) 77 { 78 scanf("%d%d%d%d",&u,&v,&l,&c); 79 add(u,v,l,c); 80 add(v,u,0,-c); 81 } 82 MCMF(s,e); 83 }
网络流之有上下界的最大流
(以后来填坑)
网络流之多源点汇点的最大流
啊这个很简单啊……
增设一个超级源点一个超级汇点
分别连接各个源点和各个汇点
同时连接的这些边容量设置为INF
正确性……
一看就是对的好吗(逃)
网络流之顶点有容量限制的最大流
这个就有个很重要的思想了:
化边为点
而这个思想不止在网络流,在很多其他地方也有重要的应用
所以这里我们就参照多源点和多汇点的最大流
将题目中的点化为边就好了啊
Emmmmmmmmm……
网络流之二分图
二分图的最大匹配
二分图匹配是二分图里面最最基础的。也有两种求解方法。
一种是匈牙利算法,此处就不再赘述了。
另一种就可以建立网络流模型,用Dinic求最大流。求出来最大流即为最大匹配。
模型的建立,就是给原本的二分图增加一个源点和一个汇点,边权全部为1,然后求最大流。
(如下图)
有一种类型的匹配题目,由于做到过,也在这里提一下。
要求三种物品匹配,给出对应关系,求最大匹配个数。
这里就要用到拆点的思想了。具体参见luogu https://www.luogu.org/problemnew/show/1231
若要求一组最大匹配可行方案,则可以循环看边的流量是否为0。
二分图的覆盖集
覆盖集:对于每条边,至少选一个端点,即至多不选一个端点。
1、 点权之和最小的覆盖
建立网络流模型:
源点--X点:容量为X点权 X点--Y点:容量为INF Y点到汇点:容量为Y点权
证明:什么叫覆盖集?对于每条边,其两端点至少有一个被选中。而割的定义为:任何一条源到汇的路径不连通。而X-Y边肯定不是属于最小割(INF)。故任何一条X-Y边一定和源点或汇点之一有且仅有一条连边。毕竟反正路径都不连通达到割的要求了,多割一条也没什么用。故二分图的最小割是点权之和最小的覆盖集。
2、 顶点数最多且点权之和尽量大的覆盖
建立网络流模型:
源点--X点:容量为1,费用为点权相反数
X点--Y点:容量为INF,费用为0
Y点到汇点:容量为1,费用为点权相反数
二分图的独立集
独立集:对于每条边,至多选一个端点,即至少不选一个端点。
最大匹配=最小覆盖=总点数-最大独立集
最大独立集和最小覆盖集是互补问题。
求最大独立集,等价于求其补集,也就是说每条边刨出至少一个端点,并且刨出的点的权和最小,这样才使剩下的最多。|最大独立集|+|最小覆盖集|=所有点的权值之和。
网络流之常见模型
1、 二分图
上面有……
2、 最大权闭合子图
所谓闭合图,就是在一张图中选出一个点的集合,保证这些点的出边所连向的点也在该集合中。最大权闭合子图指点权值最大的闭合子图。
这一性质类似这道题目的要求:
s与所有正权值的点相连,所有负权值的点与t相连。这些边的容量设为点的权值。若一个『实验』需要某个『仪器』,就在它们之间连一条无穷大的边。
最后的『收益』是用『总收益』减去『损失』(摘自gty学长课件)
裸题:luoguP3140
不明白就把样例画出来对着图理解……
Update:突然觉得当成最小割理解可能好理解
3、 DAG的最小路径覆盖
其实这个也是用二分图实现的。可以发现,每个点除了终点外,都有且仅有一条出边。
如果无匹配,显然要n条路径才能覆盖所有点,两个点匹配意味着将可以把它们用一条路径覆盖,路径数就可以减1(hzwer)
建立二分图求最大匹配即可。
4、 最多/最大权不相交路径
瞎拆点然后边的容量乱搞限制一下就好了。
5、 最短路
6、 区间k覆盖
http://blog.csdn.net/LOI_DQS/article/details/50847776
对于blog里的二方法,每个区间连了一条费用为长度相反数的边,所以跑这条路肯定是要比跑那些费用为0的路更优。不过由于源点和汇点的限制,如果覆盖超过k,则强制取k。
7、 二分法
例如HNOI2007紧急疏散,看看题解就很好懂了。
当然有时候也用枚举代替二分