1.题目选择
本次作业我选择的是题目1最大连续子数组和(最大子段和)问题: 给定n个整数(可能为负数)组成的序列a[ 1 ],a[ 2 ],a[ 3 ],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为:
Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如,当(a[ 1 ],a[ 2 ],a[ 3 ],a[ 4 ],a[ 5 ],a[ 6 ])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
2.算法分析
根据作业中所给的博客参考,我选择了材料中的暴力解法:
对数组内每一个数A[i]进行遍历,然后遍历以它们为起点的子数组,比较各个子数组的大小,找到最大连续子数组。此程序的时间复杂度为O(n3)。
流程图
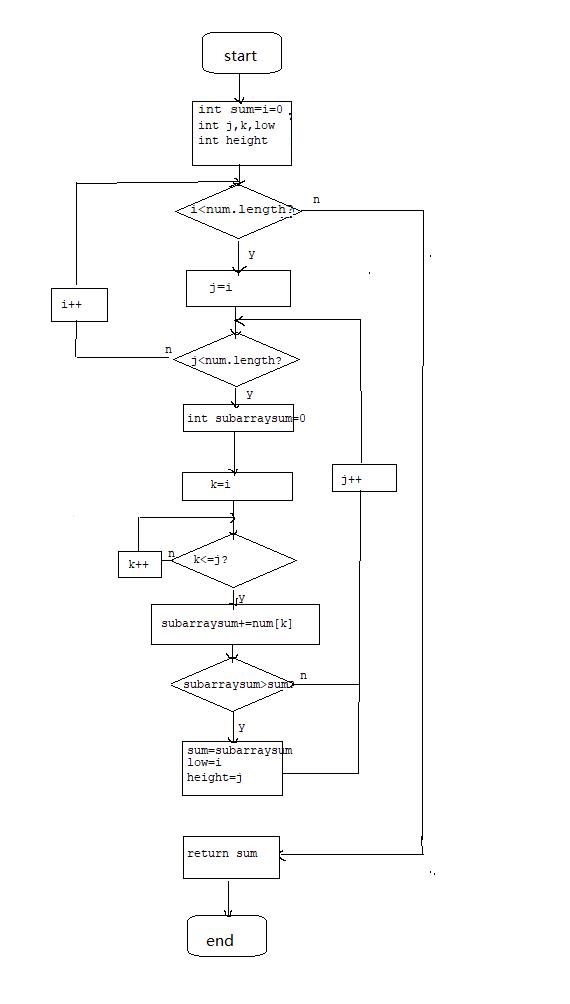
其实本来想用markdown直接画的,结果不会用,最后用的画图来解决这个问题,虽然的确是不太美观。
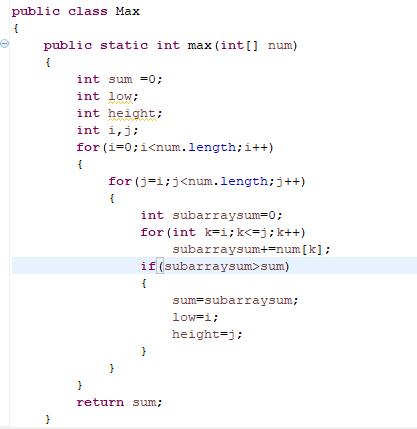
3.程序截图
以下是主要程序部分截图,有了材料给的例子,其实还蛮好理解:
4.测试结果
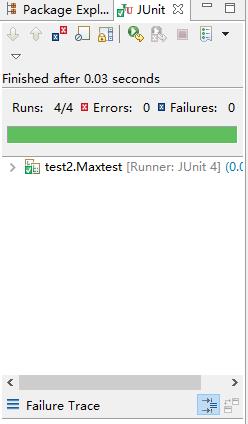
以下是测试程序截图,我用了判定/条件覆盖,共四个测试样例:全部负数;全部正数;以及两个不同测试样例;

测试结果如下:
5.总结
老实说,这道题对我来说最难的并不是程序的设计这方面,因为有了老师给的例子,只要思考一下就可以理解,真正难道我的其实是这点:我对eclipse实在是太不了解了。以前只是单纯的用C来写程序,第二次作业的完成也全是材料的功劳,等到自己再去用一遍eclipse的时候,发现并没有那么得心应手,但是还不甘心就这么放弃。后来还是通过别的同学帮助以及自己再去复习第二次作业的过程才搞定的,真的是感触颇深。通过这次教训,更加了解了自己的不足,希望以后可以通过练习,彻底熟悉这种方法。
附件:代码网址