莫队算法~讲解
Posted Misaka_Azusa
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了莫队算法~讲解相关的知识,希望对你有一定的参考价值。
用了大约1h搞定了基础的莫队算法。写篇博客算是检验下自己的学习成果。
一.什么是莫队算法?
莫队算法是用来处理一类无修改的离线区间询问问题。——(摘自前国家队队长莫涛在知乎上对莫队算法的解释。)
莫队算法是前国家队队长莫涛在比赛的时候想出来的算法。
传说中能解决一切区间处理问题的莫队算法。
准确的说,是离线区间问题。但是现在的莫队被拓展到了有树上莫队,带修莫队(即带修改的莫队)。这里只先讲普通的莫队。
还有一点,重要的事情说三遍!莫队不是提莫队长!莫队不是提莫队长!!莫队不是提莫队长!!!

二.为什么要使用莫队算法?
看一个例题:给定一个n(n<50000)元素序列,有m(m<200000)个离线查询。每次查询一个区间L~R,问每个元素出现次数为k的有几个。(必须恰好是k,不能大于也不能小于)
我们很容易想到用线段树或者树状数组直接做,但是我们想,如果是用线段树或者树状数组做而且我们不会优化的话(请dalao无视掉,您可以直接线段树做了。)每次修改和维护会很麻烦,线
段树和树状数组的优势体现不出来。
这时候就要使用莫队算法了。
三.莫队算法的思想怎么理解?
接着上面的例题,直接暴力怎么样??
肯定会T的啊。(luogu P1972 [SDOI2009]HH的项链 原数据居然可以mn模拟过......当然现在不行了)
但是如果这个暴力我们给优化一下呢?
我们想,有两个指针curL和curR,curL指向L,curR指向R。
L和R是一个区间的左右两端点。
利用cnt[]记录每个数出现的次数,每次只是cnt[a[curL]] cnt[a[curR]]修改。
举个栗子:

我们现在处理了curL—curR区间内的数据,现在左右移动,比如curL到curL-1,只需要更新上一个新的3,即curL-1。
那么curL到curL+1,我们只需要去除掉当前curL的值。因为curL+1是已经维护好了的。
curR同理,但是要注意方向哦!curR到curR+1是更新,curR到cur-1是去除。
我们先计算一个区间[curL curR]的answer,这样的话,我们就可以用O(1)转移到[curL-1 curR] [curL+1 curR] [curL curR+1] [curL curR-1]上来并且求出这些区间的answer。
我们利用curL和curR,就可以移动到我们所需要求的[L R]上啦~
这样做会快很多,但是......
如果有个**数据,让你在每个L和R间来回跑,而且跨度很大呢??
我们每次只动一步,岂不是又T了??
但是这其实就是莫队算法的核心了。我们的莫队算法还有优化。
这就是莫队算法最精明的地方(我认为的qwq),也正是有了这个优化,莫队算法被称为:优雅的暴力
我们想,因为每次查询是离线的,所以我们先给每次的查询排一个序。
排序的方法是分块。
我们把所有的元素分成多个块(即分块)。分了块跑的会更快。再按照右端点从小到大,左端点块编号相同按右端点从小到大。
这样对于不同的查询
例如:
我们有长度为9的序列。
1 2 3 4 5 6 7 8 9 分为1——3 4——6 7——9
查询有7组。[1 2] [2 1000] [1 3] [6 9] [5 8] [3 8] [8 9]
排序后就是:[1 2] [1 3] [3 8] [2 1000] | [5 8] [6 9] | [8 9]
然后我们按照这个顺序移动指针就好啦~
这样,不断地移动端点指针+精妙的排序,就是普通莫队的思想啦~
时间复杂度证明
关于时间复杂度的证明:给一个角度,其实从不同的角度看,证法很多: 对于左端点在一个块中时,右端点最坏情况是从尽量左到尽量右,所以右端点跳时间复杂度O(n),左端点一共可以在n0.5个块中,所以总时间复杂度O(n*n0.5) = (n1.5)。
四.具体代码实现:
1.对于每组查询的记录和排序:
l,r为左右区间编号,p是第几组查询的编号
1 struct query{ 2 int l, r, p; 3 }e[maxn]; 4 5 bool cmp(query a, query b) 6 { 7 return (a.l/bl) == (b.l/bl) ? a.r < b.r : a.l < b.l; 8 }
2.处理和初始变量:
answer就是所求答案,bl是分块数量,a[]是原序列,ans[]是记录原查询序列下的答案,cnt[]是记录对于每个数i,cnt[i]表示i出现过的次数,curL和curR不再解释,nmk题意要求。
1 int answer, a[maxn], m, n, bl, ans[maxn], cnt[maxn], k, curL = 1, curR = 0; 2 void add(int pos)//添加 3 { 4 //do sth... 5 } 6 void remove(int pos)//去除 7 { 8 //do sth... 9 } 10 //一般写法都是边处理 边根据处理求答案。cnt[a[pos]]就是在pos位置上原序列a出现的次数。
3.主体部分及输出:
预处理查询编号,用四个while移动指针顺便处理。
在这里着重说下四个while
我们设想有一条数轴:
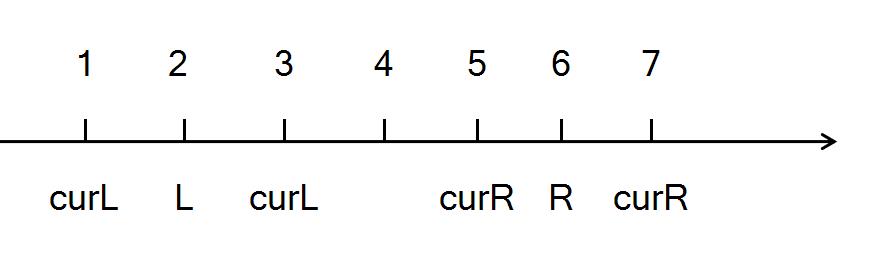
当curL < L 时,我们当前curL是已经处理好的了。所以remove时先去除当前curL再++
当curL > L 时,我们当前curL是已经处理好的了。所以 add 时先--再加上改后curL
当curR > R 时,我们当前curR是已经处理好的了。所以remove时先去除当前curR再--
当curR < R 时,我们当前curR是已经处理好的了。所以 add 时先++再加上改后curR
1 n = read(); m = read(); k = read(); 2 bl = sqrt(n); 3 4 for(int i = 1; i <= n; i++) 5 a[i] = read(); 6 7 for(int i = 1; i <= m; i++) 8 { 9 e[i].l = read(); e[i].r = read(); 10 e[i].p = i; 11 } 12 13 sort(e+1,e+1+m,cmp); 14 15 for(int i = 1; i <= m; i++) 16 { 17 int L = e[i].l, R = e[i].r; 18 while(curL < L) 19 remove(curL++); 20 while(curL > L) 21 add(--curL); 22 while(curR > R) 23 remove(curR--); 24 while(curR < R) 25 add(++curR); 26 ans[e[i].p] = answer; 27 } 28 for(int i = 1; i <= m; i++) 29 printf("%d\\n",ans[i]); 30 return 0;
五.实战莫队:
【luogu P1972 [SDOI2009]HH的项链】
https://www.luogu.org/problemnew/show/P1972
因为原来数据被大模拟过了,所以数组50000要多开。add和remove根据不同情况处理,如果当前有相同的了再++肯定不是1,如果当前相同的不止一个,remove--的时候肯定不是0,不会造成影响。反之则可以判断有多少是不同元素。
1 //HH的项链 2 #include <cstdio> 3 #include <algorithm> 4 #include <iostream> 5 #include <cmath> 6 using namespace std; 7 const int maxn = 200001; 8 const int maxm = 500001; 9 int m, n, bl, answer, curL = 1, curR = 0, ans[maxn], a[maxn], cnt[maxm];//a是原序列 cnt是记录每个数字出现的次数 10 inline int read() 11 { 12 int k=0; 13 char c; 14 c=getchar(); 15 while(!isdigit(c))c=getchar(); 16 while(isdigit(c)){k=(k<<3)+(k<<1)+c-\'0\';c=getchar();} 17 return k; 18 } 19 struct query{ 20 int l, r, p;//l 左区间 r 右区间 p 位置的编号 21 /*friend bool operator < ( query a, query b ) { 22 return (a.l/bl) == (b.l/bl) ? a.r < b.r : a.l<b.l ; 23 }*/ 24 }e[maxn]; 25 bool cmp(query a, query b) 26 { 27 return (a.l/bl) == (b.l/bl) ? a.r < b.r : a.l<b.l; 28 } 29 void add(int pos) 30 { 31 if((++cnt[a[pos]]) == 1) ++answer; 32 } 33 void remove(int pos) 34 { 35 if((--cnt[a[pos]]) == 0) --answer; 36 } 37 int main() 38 { 39 n = read(); 40 for(int i = 1; i <= n; i++) 41 a[i] = read(); 42 43 m = read(); 44 45 bl = sqrt(n); 46 47 for(int i = 1; i <= m; i++) 48 { 49 e[i].l = read(); e[i].r = read(); 50 e[i].p = i; 51 } 52 sort(e+1,e+1+m,cmp); 53 54 for(int i = 1; i <= m; i++) 55 { 56 int L = e[i].l, R = e[i].r; 57 while(curL < L) 58 remove(curL++); 59 while(curL > L) 60 add(--curL); 61 while(curR > R) 62 remove(curR--); 63 while(curR < R) 64 add(++curR); 65 ans[e[i].p] = answer; 66 } 67 for(int i = 1; i <= m; i++) 68 printf("%d\\n",ans[i]); 69 return 0; 70 }
【luogu P2709 小B的询问】
https://www.luogu.org/problemnew/show/P2709#sub
add和remove对于平方相加减的运算利用完全平方式逆回去。
1^2 = 1;
2^2 = (1+1)^2 = 1 + 1*2 + 1;
3^2 = (1+2)^2 = 1 + 2*2 + 4;
4^2 = (1+3)^2 = 1 + 3*2 + 9;
......
//小B的询问 #include <cstdio> #include <algorithm> #include <iostream> #include <cmath> using namespace std; const int maxn = 50001; int answer, a[maxn], m, n, bl, ans[maxn], cnt[maxn], k, curL = 1, curR = 0; void add(int pos) { answer+=(((cnt[a[pos]]++)<<1)+1);//完全平方式展开 } void remove(int pos) { answer-=(((--cnt[a[pos]])<<1)+1);//完全平方式展开 } inline int read() { int k=0; char c; c=getchar(); while(!isdigit(c))c=getchar(); while(isdigit(c)){k=(k<<3)+(k<<1)+c-\'0\';c=getchar();} return k; } struct query{ int l, r, p; }e[maxn]; bool cmp(query a, query b) { return (a.l/bl) == (b.l/bl) ? a.r < b.r : a.l < b.l; } int main() { n = read(); m = read(); k = read(); bl = sqrt(n); for(int i = 1; i <= n; i++) a[i] = read(); for(int i = 1; i <= m; i++) { e[i].l = read(); e[i].r = read(); e[i].p = i; } sort(e+1,e+1+m,cmp); for(int i = 1; i <= m; i++) { int L = e[i].l, R = e[i].r; while(curL < L) remove(curL++); while(curL > L) add(--curL); while(curR > R) remove(curR--); while(curR < R) add(++curR); ans[e[i].p] = answer; } for(int i = 1; i <= m; i++) printf("%d\\n",ans[i]); return 0; }
这两个题我都用了快读在里面。可以摘下来当板子背。
最后!我要吐槽一句!!luogu试炼场线段树和树状数组的题!我线段树一个也过不了!(我真是太蒟蒻了)所以还是莫队大法好!
这是几篇我学莫队时参考的博客,如果觉得我讲的不够详细,可以借鉴。
https://blog.csdn.net/wzw1376124061/article/details/67640410
以上是关于莫队算法~讲解的主要内容,如果未能解决你的问题,请参考以下文章