poj1734（floyd求最小环）

Posted 2020-10-29 lmjer

Sightseeing trip

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 7483		Accepted: 2827		Special Judge

Description

There is a travel agency in Adelton town on Zanzibar island. It has decided to offer its clients, besides many other attractions, sightseeing the town. To earn as much as possible from this attraction, the agency has accepted a shrewd decision: it is necessary to find the shortest route which begins and ends at the same place. Your task is to write a program which finds such a route.

In the town there are N crossing points numbered from 1 to N and M two-way roads numbered from 1 to M. Two crossing points can be connected by multiple roads, but no road connects a crossing point with itself. Each sightseeing route is a sequence of road numbers y_1, ..., y_k, k>2. The road y_i (1<=i<=k-1) connects crossing points x_i and x_{i+1}, the road y_k connects crossing points x_k and x_1. All the numbers x_1,...,x_k should be different.The length of the sightseeing route is the sum of the lengths of all roads on the sightseeing route, i.e. L(y_1)+L(y_2)+...+L(y_k) where L(y_i) is the length of the road y_i (1<=i<=k). Your program has to find such a sightseeing route, the length of which is minimal, or to specify that it is not possible,because there is no sightseeing route in the town.

Input

The first line of input contains two positive integers: the number of crossing points N<=100 and the number of roads M<=10000. Each of the next M lines describes one road. It contains 3 positive integers: the number of its first crossing point, the number of the second one, and the length of the road (a positive integer less than 500).

Output

There is only one line in output. It contains either a string \'No solution.\' in case there isn\'t any sightseeing route, or it contains the numbers of all crossing points on the shortest sightseeing route in the order how to pass them (i.e. the numbers x_1 to x_k from our definition of a sightseeing route), separated by single spaces. If there are multiple sightseeing routes of the minimal length, you can output any one of them.

Sample Input

5 7
1 4 1
1 3 300
3 1 10
1 2 16
2 3 100
2 5 15
5 3 20

Sample Output

1 3 5 2

Source

CEOI 1999

 

此题为求最小环问题

 

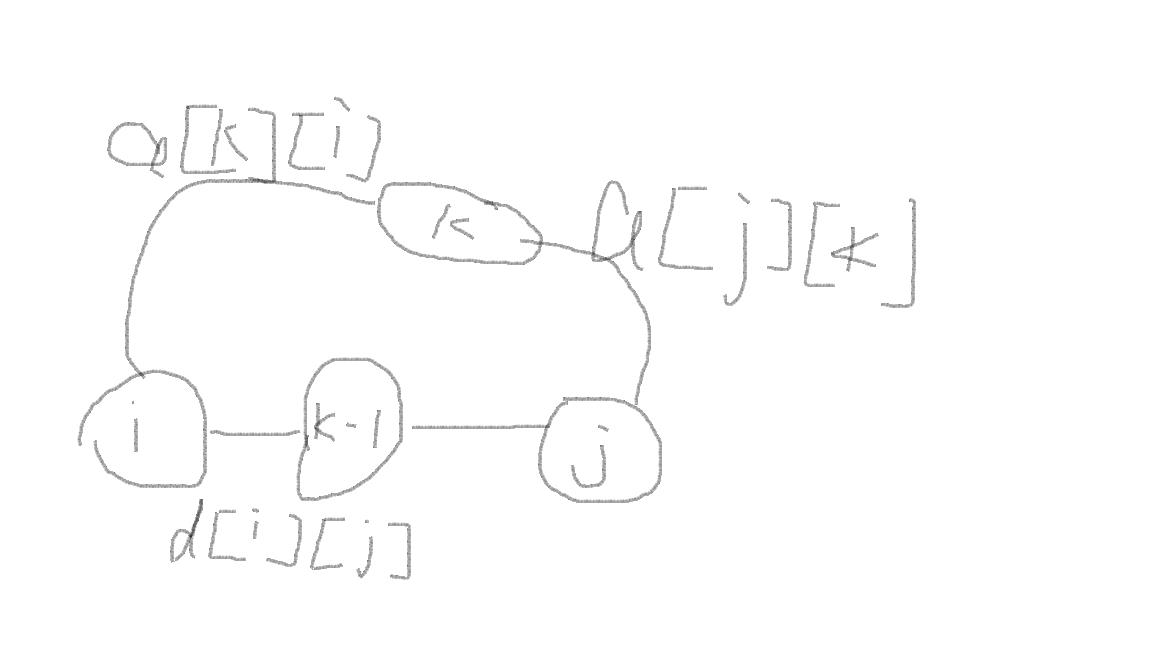
考虑的floyd中 ，d[i][j]表示求经过不超过k-1的最短路

所以，最小环可由min{d[i][j]+a[k][i]+a[j][k]}求的；

如图

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;

const int maxn=300+10;
int ans=0x3f3f3f3f;
int a[maxn][maxn],d[maxn][maxn],pos[maxn][maxn];
vector<int>path;

void getpath(int x,int y){
     if(pos[x][y]==0) return ;
     getpath(x,pos[x][y]);
     path.push_back(pos[x][y]);
     getpath(pos[x][y],y);
}

int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    int u,v,w;
    memset(d,0x3f3f3f3f,sizeof(d));
    memset(a,0x3f3f3f3f,sizeof(a));
    while(m--){
       scanf("%d%d%d",&u,&v,&w);
       a[u][v]=a[v][u]=d[u][v]=d[v][u]=min(a[u][v],w);
    }
    for (int k=1;k<=n;k++){
        for (int i=1;i<k;i++){
            for (int j=i+1;j<k;j++){
                if((long long)d[i][j]+a[k][i]+a[j][k]<ans){
                    ans=d[i][j]+a[k][i]+a[j][k];
                    path.clear();
                    path.push_back(i);
                    getpath(i,j);
                    path.push_back(j);
                    path.push_back(k);
                }
            }
        }
        for (int i=1;i<=n;i++){
            for (int j=1;j<=n;j++){
                if(d[i][j]>d[i][k]+d[k][j]){
                    d[i][j]=d[i][k]+d[k][j];
                    pos[i][j]=k;
                }
            }
        }
    }
    if(ans==0x3f3f3f3f) printf("No solution.\\n");
    else {
        for (int i=0;i<path.size();i++){
            printf("%d ",path[i]);
        }
        printf("\\n");
    }
 return 0;
}