深度学习——神经网络
Posted 记性不好,多记记吧
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了深度学习——神经网络相关的知识,希望对你有一定的参考价值。
目录
- 神经网络表示
- 激活函数
- 不要把所有参数都初始化为0
- 反向计算求导
一、神经网络表示
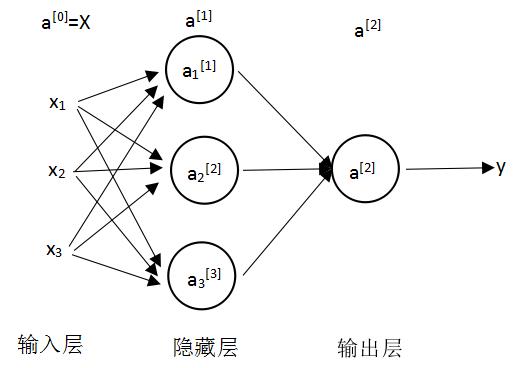

神经网络层数= 隐藏数+输出层(1)
输入不算是一层,可以说是第0层
第i层的值:W[1]可以用来表示是第1层的参数
激活值:当前层会传递给下一层的值如a[0]表示输入层会传给第一层的值
每一层中有多个神经元,然后它们可以做相同的事,比如第一层中有3个参数,用下标来区分
二、激活函数
sigmoid: $a = \\frac{1}{1+e^{-z}}$ 只用于二元分类输出层
缺点:不是以0为中心;当$x$很大/小时,梯度趋于0
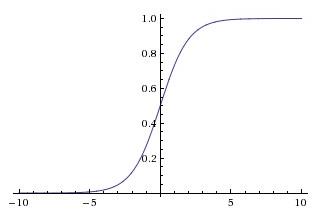
tanh: $a = \\frac{e^z - e^{-z}}{e^z + e^{-z}}$
分布以0为中心点
缺点:和sigmoid一样当z很大/小时斜率趋于0,使得梯度下降效果弱
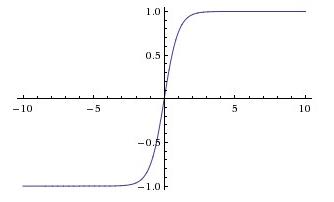
ReLU:$a = max(0,z)$ 一般会采用这个
优点:右侧是线性的,求梯度简单且收敛速度快
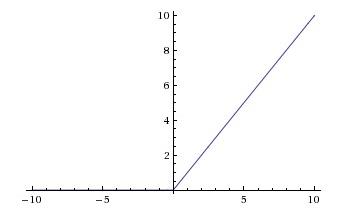
为什么要用非线性激活函数:线性函数得出的关系比较简单,不足以描述现实中复杂的关系
三、不能把所有参数都初始化为0
如果把w初始化为0,那么多个神经元的计算就会是一样的(对称性),归纳可得不管多少次后也是一样的结果,则一层中多个神经元也变得没有意义
随机初始化:W=np.randm.radn((2,2))*0.01 这里0.01是因为希望得到的W不要太大,因为激活函数在变量绝对值较大的位置变化比较平缓
四、反向计算求导
正向计算(黑色),反向求导计算(红色)
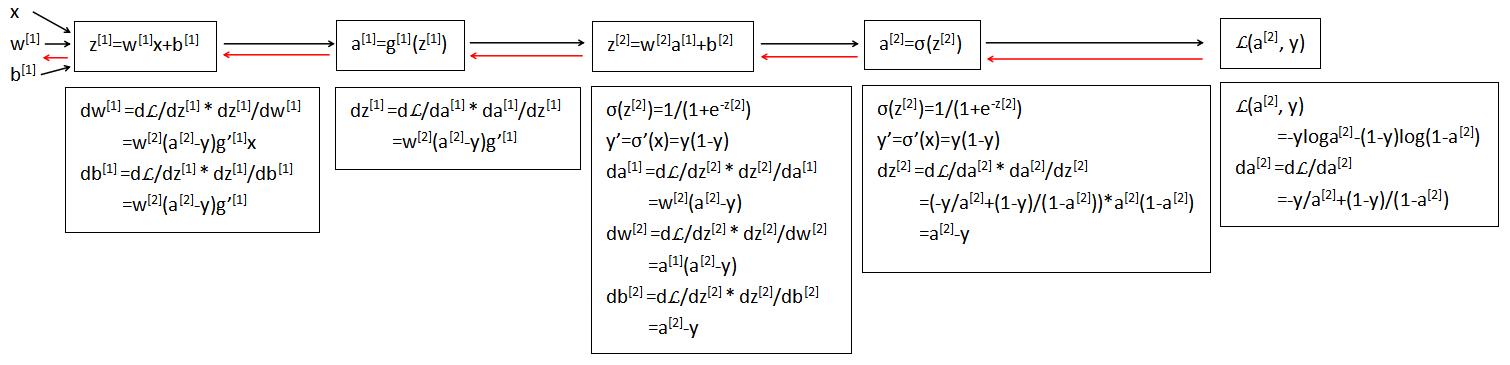
以上是关于深度学习——神经网络的主要内容,如果未能解决你的问题,请参考以下文章