蓝桥杯剪邮票

Posted 2020-10-28 努力的程序媛

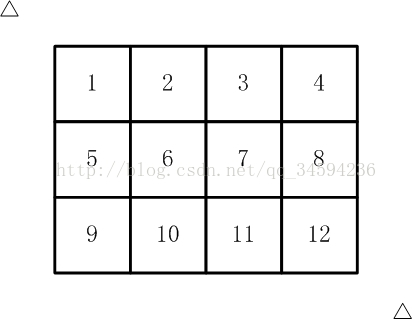
如【图1.jpg】, 有12张连在一起的12生肖的邮票。

现在你要从中剪下5张来，要求必须是连着的。
（仅仅连接一个角不算相连）
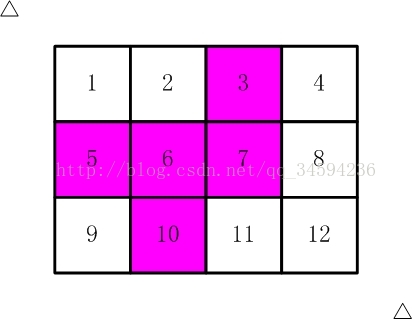
比如，【图2.jpg】，【图3.jpg】中，粉红色所示部分就是合格的剪取。

请你计算，一共有多少种不同的剪取方法。
请填写表示方案数目的整数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

题目答案：

116

 

思路：

先枚举一下组合数，也就是C（12,5）=792种可能，然后判断每一种可能是否连通，那怎么判连通呢？因为我的num[1]~num[5]存储的是那五个数，所以我们判断如果从num[1]能走到num[2]~num[5]中的任意一个点的话，就证明这一片区域是连通的，用一个flag变量来记录从num[1]走到其他点成功的次数，总共有四种可能（1~2,1~3,1~4,1~5）,如果都能走到的话，那么flag的值应该是4，这样的话就证明连通一个去区域了,所以就把sum++，最后输出sum的值就行,(j,k)代表的是起始点的坐标，（p,q）代表终点的坐标，注意实时更新

代码

#include <iostream>
#include <cstring>
using namespace std;
const int n=12,m=5;
int sum=0,j,k,q,p,flag;  //sum计总数,(j,k)代表的是起始点的坐标，（p,q）代表终点的坐标,注意实时更新
int a[20];  　　　　　　　　//存放组合数
int s[3][4];　　　　　　　　//标记是否走过
int go[4][2]={           //右下左上四个方向
              {0,1},
              {1,0},
              {0,-1},
              {-1,0},
              };
int judge(int x,int y) //判断是否在五个点之内
{
    int k=x*4+y+1;
    for(int i=0;i<5;i++)
        if(a[i]==k)
          return 1;
    return 0;
}
void dfs(int x,int y) //判断联通
{
    if(x==p&&y==q)
    {
        flag++;
    
        return;
    }
    for(int i=0;i<=3;i++)
    {
        int xx=x+go[i][0];
        int yy=y+go[i][1];

        if(xx>=0&&xx<3&&yy>=0&&yy<4&&judge(xx,yy)&&s[xx][yy]==0)
        {
            s[xx][yy]=1;
            dfs(xx,yy);
        }
    }
    return;
}
void init(int d,int cnt) //生成组合数
{
    if(cnt==m)
    {
        flag=0;
        j=(a[0]-1)/4;
        if(a[0]%4==0)
            k=3;
        else
        k=a[0]%4-1;
        for(int i=1;i<m;i++)
        {
            p=(a[i]-1)/4;
            if(a[i]%4==0)
            q=3;
            else
            q=a[i]%4-1;
            memset(s,0,sizeof(s)); //注意这里
            s[j][k]=1;
            dfs(j,k);
        }
        if(flag==4)
            sum++;  
        return;
    }
    for(int i=d;i<=n;i++)
    {
        a[cnt]=i;
        init(i+1,cnt+1);
    }
    return ;
}
int main()
{
   memset(book,0,sizeof(book));
   memset(s,0,sizeof(s));
   init(1,0);
   cout<<sum;
}

这题卡了我一整天,终于A了,但我却一点都高兴不起来,

什么嘛,我怎么这么简单的题都做不对

卡在坐标上,卡在变量名写错上

我,,,,

真的是自己太急躁了吗

唉.