神经网络反向传播
首先理解一个基础前提,神经网络只是一个嵌套的,非线性函数(激活函数)复合线性函数的函数。对其优化,也同一般机器学习算法的目标函数优化一样,可以用梯度下降等算法对所有函数参数进行优化。
但因为前馈神经网络的函数嵌套关系,对其优化求偏导时,存在一个沿着网络反方向的链式关系。
以一个两个隐藏层的网络为例:
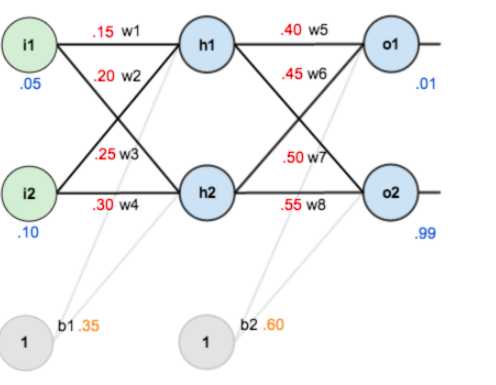
对最终的误差函数求偏导,沿着嵌套函数的方向,存在求偏导的一个链条,如下图:
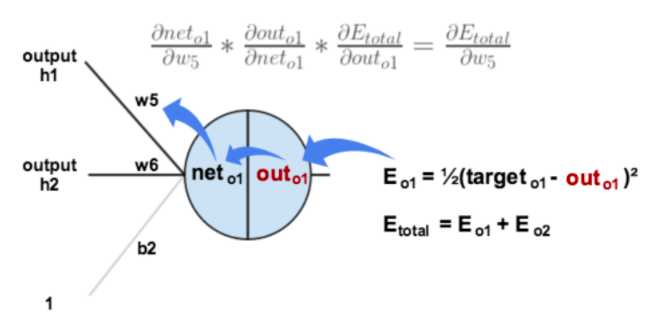
沿着这个链条去求得误差函数相对w5的偏导(也就是梯度),就可以对w5进行优化更新。到这儿看起来也只是体现为普通的求梯度去优化目标函数,虽然存在链式的求偏导过程。而反向传播的优势在于,沿网络反方向求偏导的过程中,前期已经的计算的偏导值可以为后期传播到的节点求偏导过程所用。
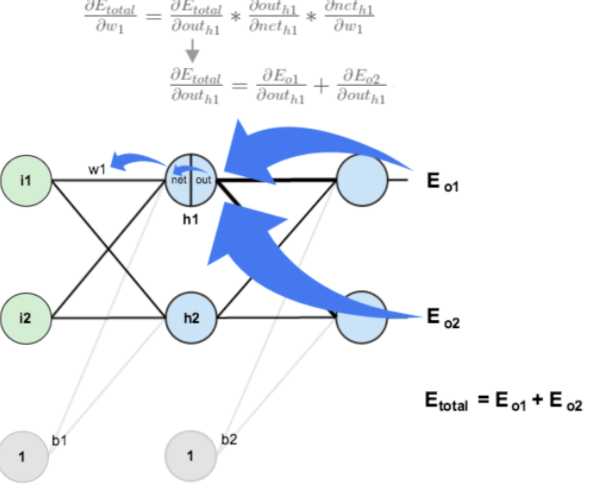
例如下图,继续计算目标函数对w1的偏导的过程中,之前计算w5偏导的时候,已经得到的链条中偏导值可以继续使用,而不用相对w1再次重新计算,从而提高整体优化速度。