决策树（chap3）Machine Learning In Action学习笔记

Posted 2020-07-08 woaielf

优点：计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据。

缺点：可能会产生过度匹配问题。

适用数据类型：数值型（必须离散化）和标称型。

决策树创建分支的伪代码函数createBranch()：

检测数据集中的每个子项是否属于同一分类：

    If so return 类标签；

    Else

        寻找划分数据集的最好特征

        划分数据集

        创建分支节点

            for 每个划分的子集

                调用函数createBranch并增加返回结果到分支节点中

        return 分支节点

决策树的一般流程 

收集数据：可以使用任何方法。

准备数据：树构造算法只适用于标称型数据，因此数值型数据必须离散化。

分析数据：可以使用任何方法，构造树完成之后，我们应该检查图形是否符合预期。

训练算法：构造树的数据结构。（ID3算法）

测试算法：使用经验树计算错误率。

使用算法：此步骤可以适用于任何监督学习算法，而使用决策树可以更好地理解数据的内在含义。

划分数据集的大原则是：将无序的数据变得更加有序。

组织杂乱无章数据的一种方法就是使用信息论度量信息。

信息增益：划分数据集之前之后信息发生的变化。（计算每个特征值划分数据集获得的信息增益，获得信息增益最高的特征就是最好的选择。）

集合信息的度量方式称为香农熵或者简称为熵（信息的期望值）。熵越大则数据越无序。

待分类的事务可能划分在多个分类之中，则符号xi 的信息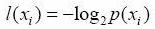： （p(xi)是选择该分类的概率）

熵（信息的期望值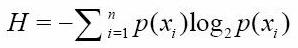）：（n是分类的数目）

对每个特征划分数据集的结果计算一次信息熵，然后判断按照哪个特征划分数据集是最好的划分方式。

递归构建决策树：

工作原理如下：得到原始数据集，然后基于最好的属性值划分数据集，由于特征值可能多于两个，因此可能存在大于两个分支的数据集划分。第一次划分之后，数据将被向下传递到树分支的下一个节点，在这个节点上，我们可以再次划分数据。因此我们可以采用递归的原则处理数据集。

递归结束的条件是：程序遍历完所有划分数据集的属性，或者每个分支下的所有实例都具有相同的分类。如果所有实例具有相同的分类，则得到一个叶子节点或者终止块。任何到达叶子节点的数据必然属于叶子节点的分类。

构造决策树是很耗时的任务，即使处理很小的数据集，如前面的样本数据，也要花费几秒的时间，如果数据集很大，将会耗费很多计算时间。然而用创建好的决策树解决分类问题，则可以很快完成。因此，为了节省计算时间，最好能够在每次执行分类时调用已经构造好的决策树。为了解决这个问题，需要使用Python模块pickle序列化对象。

本章代码：（略去画图部分，太繁琐了……）

# -*- coding:utf-8 -*-
from math import log
from numpy import *
import operator
def createDataSet():
    dataSet = [[1, 1, \'yes\'],
               [1, 1, \'yes\'],
               [1, 0, \'no\'],
               [0, 1, \'no\'],
               [0, 1, \'no\']]
    labels = [\'no surfacing\', \'flippers\']
    # change to discrete values
    return dataSet, labels
# 测量给定数据集的信息熵，度量数据的无序程度，熵越大则数据越无序。
def calcShannonEnt(dataSet):
    numEntries = len(dataSet)
    labelCounts = {}
    for featVec in dataSet:
        currentLabel = featVec[-1]
        labelCounts[currentLabel] = labelCounts.get(currentLabel, 0) + 1
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key]) / numEntries
        shannonEnt -= prob * log(prob, 2)
    return shannonEnt
# 按照给定特征划分数据集(当我们按照某个特征划分数据集时，就需要将所有符合要求的元素抽取出来)
# axis：用来划分数据集的特征(索引值), value：该特征选取的属性值(需要返回的值)
def splitDataSet(dataSet, axis, value):
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:]
            reducedFeatVec.remove(value)
            retDataSet.append(reducedFeatVec)
    return retDataSet
# 选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0
    bestFeature = -1
    for i in range(numFeatures):
        # 创建唯一的分类标签列表
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntropy = 0.0
        # 计算每种划分方式的信息熵
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet) / float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy
        # 计算最好的信息增益
        if infoGain > bestInfoGain:
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature
def majorityCnt(classList):
    classCount = {}
    for vote in classList:
        classCount[vote] = classCount.get(vote, 0) + 1
    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]
def createTree(dataSet, labels):
    classList = [example[-1] for example in dataSet]
    # 两个结束条件：类别完全相同或者遍历完所有特征
    if len(set(classList)) == 1:
        return classList[0]
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel: {}}
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
    return myTree
def classify(inputTree, featLabels, testVec):
    firstStr = inputTree.keys()[0]
    secondDict = inputTree[firstStr]
    featIndex = featLabels.index(firstStr)
    for key in secondDict.keys():
        if testVec[featIndex] == key:
            if type(secondDict[key]).__name__ == \'dict\':
                classLabel = classify(secondDict[key], featLabels, testVec)
            else:
                classLabel = secondDict[key]
    return classLabel
# 使用pickle模块存储决策树
def storeTree(inputTree, filename):
    import pickle
    fw = open(filename, \'w\')
    pickle.dump(inputTree, fw)
    fw.close()
def grabTree(filename):
    import pickle
    fr = open(filename)
    return pickle.load(fr)

参考资料：

1. Peter Harrington《机器学习实战》第三章

来自为知笔记(Wiz)