学习算法的预测误差（泛化误差），分解为三部分：bias，variance，noise。
对于测试样本x，令yD为x在数据集中的标记（可能存在噪声导致标记值和真实值不同），y为x的真实值，f(x;D)在训练集D上学得模型f在x上的输出。以回归任务为例：
学习算法的期望预测：就是在不同的数据集（同一来源）上得到的模型 f 对 x 做预测，取其平均，
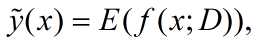
产生的方差的计算为：
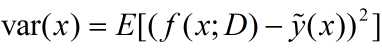
我们需要明确：方差是多个模型间的比较，而非对于一个模型而言的（多个数据集产生多个模型，理想情况下希望这些模型其实都是同一个），所以方差的定义也是对于多个数据集而言的，每个模型对于样本 x 做预测，和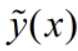
做差再求平方，再取期望得到了所谓的variance。
对于噪声定义为：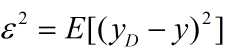
，标记值与真实值之间的平方差期望。
偏差则定义成期望输出与真实标记的差别，偏差的平方定义为：
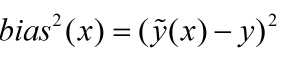
对于偏差而言，可以是单个的数据集中的偏差，也可以是多个数据集中的偏差。一般来说，variance和bias是从同一个数据集中，用科学的采样方法得到几个不同的子数据集，用这些子数据集得到的模型，就可以讨论他们的方差和偏差的情况了。
泛化误差的推理：
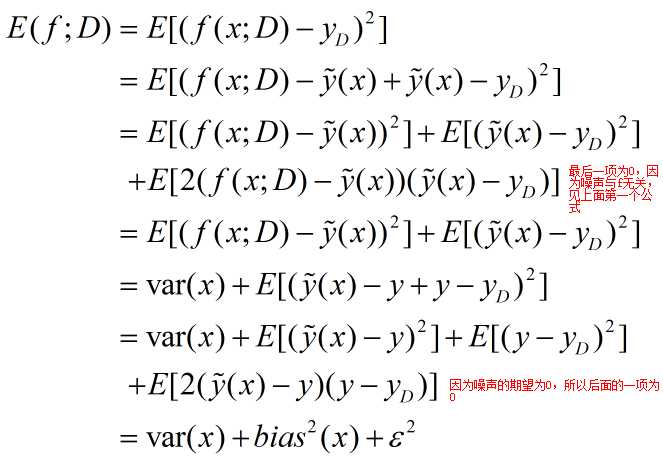
这是为了我更好的理解bias和variance而写，不知是否会有误区，参考于博客：
https://www.cnblogs.com/daguankele/p/6561419.html