一、PTA实验作业
题目一:7-1 最长连续递增子序列
给定一个顺序存储的线性表,请设计一个算法查找该线性表中最长的连续递增子序列。例如,(1,9,2,5,7,3,4,6,8,0)中最长的递增子序列为(3,4,6,8)。
1、设计思路
/*求最长递增子序列*/
定义变量 position 、len 记录子列的开始位置和长度
定义变量 maxposi 、maxlen 记录最长递增子列的位置和长度
while i < L->length
do
if 不为递增
then 重新记录子列初始位置和长度
else len++
if 当前长度 > 最大长度
then maxposi、maxlen ← position、len
end
for 0 to maxlen
顺序表 L ← 最长递增子列
end
L 的长度 ← maxlen
2、实验代码
- 主函数
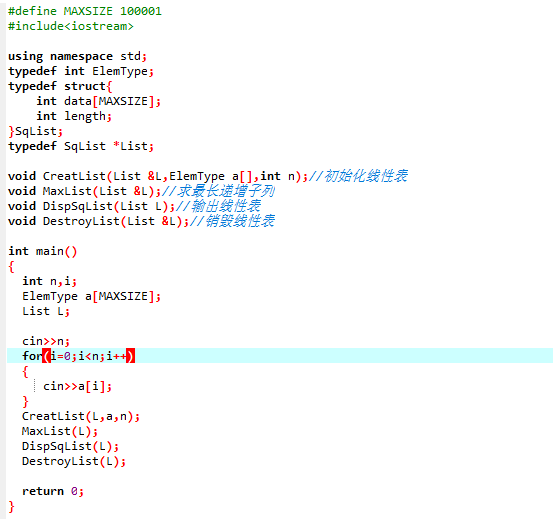
- 求最长递增子列
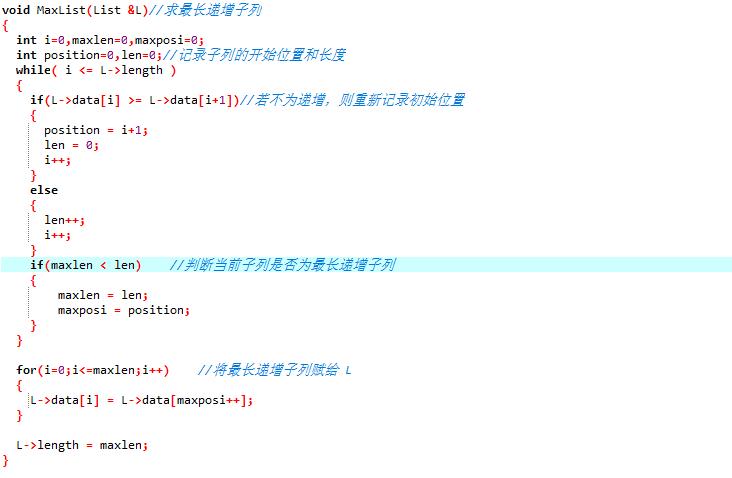
3、 遇到问题及解决方法
- 编译错误:用 c 的编译器运行 c++ 文件
解决方法:将上传选项改为 c++ - 答案错误:随机最大 n 的测试点过不去
解决方法:将#define MAXSIZE 100000改为#define MAXSIZE 100001防止数据溢出

题目二:7-3 两个有序序列的中位数
已知有两个等长的非降序序列S1, S2, 设计函数求S1与S2并集的中位数。
1、设计思路
- 1)合并链表
- 2)输出合并链表的第 n 个数 ( n 为单个链表的表长 )
/* 链表的合并 */
定义指针变量 p1 指向 L1
定义指针变量 p2 指向 L2
while p1 不空 and p2 不空
do
if ( p1->data ≤ p2->data )
then L ← p1
else L ← p2
end
L ← 剩余的 L1 or L2
2、实验代码
- 主函数

- 链表合并
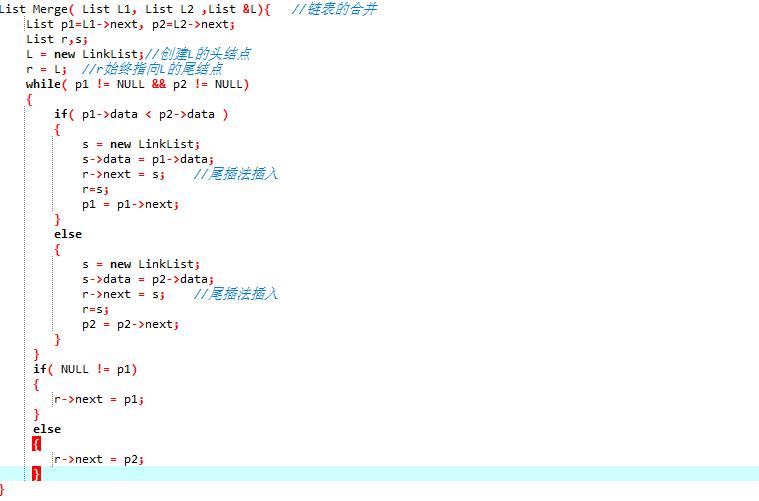
- 求中位数
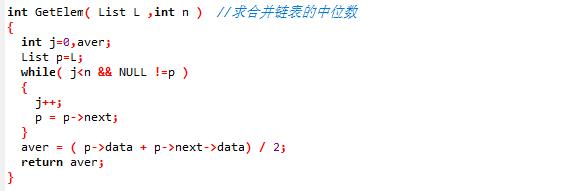
3、 遇到问题及解决方法
- 运行超时:多写了对单个子列的排序函数
解决方法:子列本为非降序,无需排序 - 编译错误:函数的声明放在了结构体之前,导致 List 未定义
解决方法:将函数声明置于结构体定义之后
题目三:7-2 一元多项式的乘法与加法运算
设计函数分别求两个一元多项式的乘积与和。
1、设计思路
/*多项式加法*/
定义结构体指针 ha hb 分别指向 链表 a b
定义结构体指针 c 用于存储新链表
定义整型变量 temp 用于判断系数是否为零
while a不空 and b不空
do
if ha->index ≠ hb->index
then 按顺序存入新链表
else 合并同类项
end
if a不为空 or b 不为空
then c ← 剩余结点
返回 c
/*多项式乘法*/
定义结构体指针 ha hb 分别指向 链表 a b
定义结构体指针 c 用于存储新链表
定义 tmpC 暂存 乘法运算结果
if a空 or b空
then 返回空的 c
while ha
do 遍历乘以 b 中元素
end
调用加法函数,进行合并同类项,并将结果赋于 c
返回 c
2、实验代码
- 主函数

- 多项式加法


- 多项式乘法

3、 遇到问题及解决方法
- 答案错误:没有考虑同类项合并问题
解决方法:增加了指数相同,系数相加的代码行 - 段错误:在
if ( p ->coeff > p->next->coeff )时没有判断 p->next 是否存在
解决方法:将循环条件while ( p )改为while ( p->next ) - 答案错误:系数为零时不输出
解决方法:判断系数非零时才加入新链表中
二、截图本周题目集的PTA最后排名
- 1.顺序表PTA排名

- 2.链表PTA排名

- 3.我的总分:2.5
2.5分(必做题全部做完,选做题做部分 )
本周学习总结
1、数据结构的学习时间和自我感觉
- 本周数据结构学习时间:对于数据结构的学习时间基本都花在打 PTA 上 ,PTA 的内容有很多不懂,花了很多时间。
- 对自己的安排不满意,觉得这样效率不高,但是 PTA 又要完成,有点赶鸭子上架的感觉。
- 对于不懂的问题,一般问同学或者是百度。
- 应该做出的改变:先巩固基本知识,再来做实际编程。
2、对线性表的认识
- 顺序表 & 优点: 对数据的访问方便,无需未表示表中元素逻辑关系而占用内存
缺点:插入和删除元素需要大量移动元素 ; 无法充分利用零碎空间,容易造成空间浪费 - 链表 & 优点:在插入、删除元素时只需要对单个结点进行操作,不需移动元素
缺点:在访问数据时需要遍历,存储密度较小
3.代码Git提交记录截图
