一、冒泡排序
1、思路:首先,列表每两个相邻的数比较大小,如果前边的比后边的大,那么这两个数就互换位置。就像是冒泡一样
2、代码关键点:
- 趟数:n-1趟
- 无序区
3、图示说明:依次类推就会得到排序结果。冒泡排序的效率还是很低的
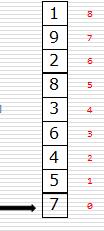
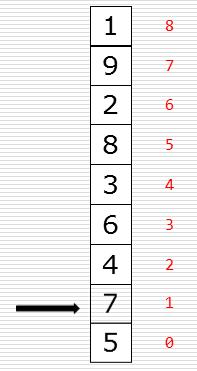
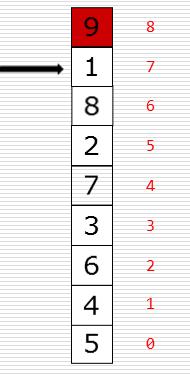
4、代码示例

# 思路:列表中两个相邻的数比较大小,如果前边的比后边的大,那么这两个就互换位置 def bubblr_sort(li): for i in range(1,len(li)-1):#表示趟数 change = True for j in range(len(li)-i): #表示无序区,无序区的范围为0,len(li)-i if li[j] > li[j+1]: li[j],li[j+1] = li[j+1],li[j] change = True if not change: return li = list(range(10)) import random random.shuffle(li) print(li) bubblr_sort(li) print(li) 冒泡排序
时间复杂度:O(n2)
二、选择排序
1、思路:一趟遍历完记录最小的数,放到第一个位置;在一趟遍历记录剩余列表中的最小的数,继续放置
2、代码关键点:
- 无序区
- 最小数的位置
3、问题:怎么选出最小的数?

import random def select_sort(li): for i in range(len(li)-1): #i 表示躺数,也表示无序区开始的位置 min_loc = i #最小数的位置 for j in range(i+1,len(li)): #i ,i+1,就是后一个位置的范围 # [9, 2, 1, 6, 5, 8, 3, 0, 7, 4] # [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] if li[j] <li[min_loc]: #两个位置进行比较,如果后面的一个比最小的那个位置还小,说明就找到最小的了 min_loc = j #找到最小的位置 li[i],li[min_loc] = li[min_loc],li[i] #吧找到的两个值进行互换位置 li = list(range(10)) random.shuffle(li) print(li) select_sort(li) print(li) 选择排序
4、时间复杂度:O(n2)
三、插入排序
1、思路:元素被分为有序区和无序区两部分。最初有序区只有一个元素。每次从无序区中选择一个元素,插入到有序区的位置,直到无序区变空。
2、代码关键点:
- 摸到的牌
- 手里的牌
3、图示说明
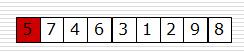

插入后:
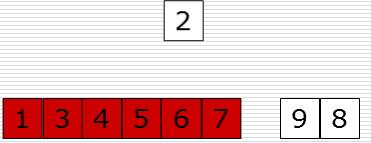
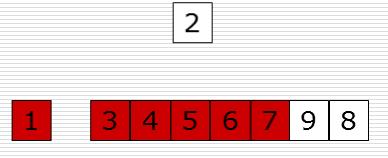

4、代码示例

1 import random 2 def insert_sort(li): 3 for i in range(1,len(li)): 4 #i 表示无序区的第一个数 5 tmp = li[i] #摸到的牌 6 j = i-1 #指向有序区最后一个位置 7 while li[j] >tmp and j>=0: 8 #循环终止条件 li[j]<=tmp and j==-1 9 li[j+1] = li[j] #向后移动 10 j-=1 11 li[j+1] = tmp 12 13 li = list(range(10)) 14 random.shuffle(li) 15 print(li) 16 insert_sort(li) 17 print(li)
四、快速排序
1、思路:1、取一个元素p(第一个元素),是元素p归位(去它该去的地方);
2、列表被p分成两部分,左边的都比p小,右边的都比p大;
3、递归完成排序
2、算法关键点
- 归位
- 递归
3、图示说明



4、怎么归并呢?先把5取出来,这时候就会有一个空位,从右边找比5小的数填充过来,现在右边有一个空位了,从左边找比5大的放到右边的空位上。依次类推,
只要left和right碰在一起,这样就找打5的位置了
如图示:
图一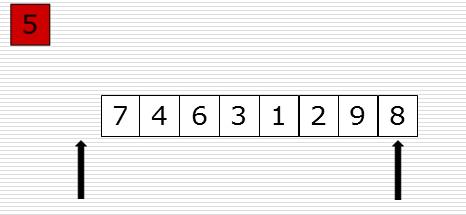 图二
图二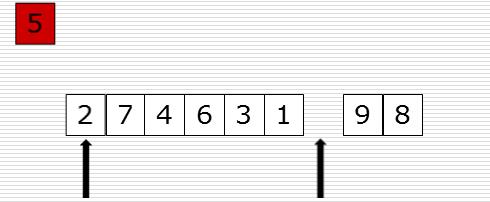
图三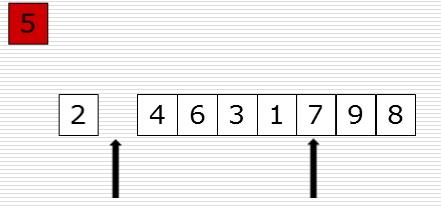 图四
图四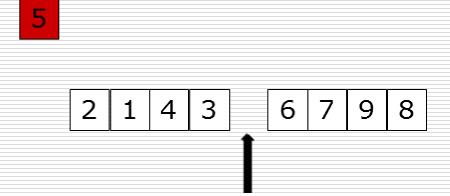
这样在把找到的5的位置放进去去ok了
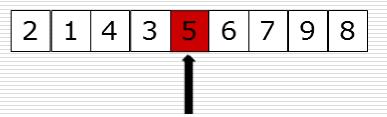
5、代码示例

1 import time 2 def wrapper(func): 3 def inner(*args,**kwargs): 4 start = time.time() 5 ret = func(*args,**kwargs) 6 end = time.time() 7 print(\'%s running time :%s\'%(func.__name__,start-end)) 8 return ret 9 return inner 10 11 12 def partition(li,left,right): 13 \'\'\'归位函数\'\'\' 14 tmp = li[left] #先把5取出来 15 while left < right: 16 while left < right and li[right] >= tmp: #如果降序排列修改li[right] <= tmp 17 right -= 1 #从右边找比5小的数,填充到5的位置 18 li[left] = li[right] 19 while left < right and li[left] <= tmp: #如果降序排列修改li[right] >= tmp 20 left += 1# 从左边找比5大的数字放在右边的空位 21 li[right] = li[left] 22 li[left] = tmp #当跳出循环条件的时候说明找到了,并且把拿出来的5在放进去 23 return left 24 25 26 def _quick_sort(li,left,right): 27 \'\'\'快速排序的两个关键点:归位,递归\'\'\' 28 if left < right: #至少有两个元素,才能进行递归 29 mid = partition(li,left,right) #找到归位的位置 30 _quick_sort(li,left,mid-1) #递归,右边的-1 31 _quick_sort(li,mid+1,right) #递归,左边的+1 32 33 @wrapper 34 def quick_sort(li): 35 return _quick_sort(li, 0, len(li)-1) 36 37 @wrapper 38 def sys_sort(li): 39 \'\'\'系统排序\'\'\' 40 li.sort() 41 42 import random 43 li = list(range(100000)) 44 random.shuffle(li) 45 # print(li) 46 quick_sort(li) 47 # print(li) 48 49 sys_sort(li) 50 51 #结论:系统的排序要比快排的时间快的多 52 # quick_sort running time :-0.6240355968475342 53 # sys_sort running time :-0.002000093460083008
6、快速排序的时间复杂度O(nlogn)
五、堆排序
有关对的了解:http://www.cnblogs.com/haiyan123/p/8400537.html
1、堆排序过程:
- 1、建立堆
- 2、得到堆顶元素,为最大元素
- 3、去掉堆顶,将堆最后一个元素放在堆顶,此时可通过一次调整重新使堆有序
- 4、堆顶元素为第二大元素
- 5、重复步骤3,直到堆变空
代码示例

1 import random 2 3 def _sift(li, low, high): 4 """ 5 :param li: 6 :param low: 堆根节点的位置 7 :param high: 堆最有一个节点的位置 8 :return: 9 """ 10 i = low # 父亲的位置 11 j = 2 * i + 1 # 孩子的位置 12 tmp = li[low] # 原省长 13 while j <= high: 14 if j + 1 <= high and li[j + 1] > li[j]: # 如果右孩子存在并且右孩子更大 15 j += 1 16 if tmp < li[j]: # 如果原省长比孩子小 17 li[i] = li[j] # 把孩子向上移动一层 18 i = j 19 j = 2 * i + 1 20 else: 21 li[i] = tmp # 省长放到对应的位置上(干部) 22 break 23 else: 24 li[i] = tmp # 省长放到对应的位置上(村民/叶子节点) 25 26 27 def sift(li, low, high): 28 """ 29 :param li: 30 :param low: 堆根节点的位置 31 :param high: 堆最有一个节点的位置 32 :return: 33 """ 34 i = low # 父亲的位置 35 j = 2 * i + 1 # 孩子的位置 36 tmp = li[low] # 原省长 37 while j <= high: 38 if j + 1 <= high and li[j+1] > li[j]: # 如果右孩子存在并且右孩子更大 39 j += 1 40 if tmp < li[j]: # 如果原省长比孩子小 41 li[i] = li[j] # 把孩子向上移动一层 42 i = j 43 j = 2 * i + 1 44 else: 45 break 46 li[i] = tmp 47 48 49 50 def heap_sort(li): 51 n = len(li) 52 # 1. 建堆 53 for i in range(n//2-1, -1, -1): 54 sift(li, i, n-1) 55 # 2. 挨个出数 56 for j in range(n-1, -1, -1): # j表示堆最后一个元素的位置 57 li[0], li[j] = li[j], li[0] 58 # 堆的大小少了一个元素 (j-1) 59 sift(li, 0, j-1) 60 61 62 li = list(range(10)) 63 random.shuffle(li) 64 print(li) 65 heap_sort(li) 66 print(li) 67 68 # li=[2,9,7,8,5,0,1,6,4,3] 69 # sift(li, 0, len(li)-1) 70 # print(li)
六、归并排序
假设现在的列表分两段有序,如何将其合成为一个有序列表。这种操作称为一次归并
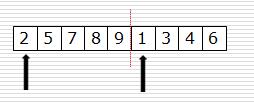
1、思路:
2、归并关键字
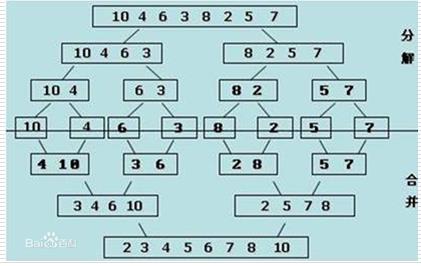
- 分解:将列表越分越小,直至分成一个元素
- 终止条件:一个元素是有序的
- 合并:将两个有序列表归并,列表越来越大
3、图实示例:https://www.cnblogs.com/chengxiao/p/6194356.html
4、代码示例:

1 import random 2 def merge(li, low, mid, high): 3 # 一次归并 4 \'\'\' 5 :param li: 列表 6 :param low: 起始位置 7 :param mid: 按照那个位置分 8 :param high: 最后位置 9 :return: 10 \'\'\' 11 i = low 12 j = mid + 1 13 ltmp = [] 14 while i <= mid and j <= high: 15 if li[i] < li[j]: 16 ltmp.append(li[i]) 17 i += 1 18 else: 19 ltmp.append(li[j]) 20 j += 1 21 while i <= mid: 22 ltmp.append(li[i]) 23 i += 1 24 while j <= high: 25 ltmp.append(li[j]) 26 j += 1 27 li[low:high+1] = ltmp 28 29 30 def _merge_sort(li, low, high): 31 if low < high: # 至少两个元素 32 mid = (low + high) // 2 33 _merge_sort(li, low, mid) 34 _merge_sort(li, mid+1, high) 35 merge(li, low, mid, high) 36 print(li[low:high+1]) 37 38 39 def merge_sort(li): 40 return _merge_sort(li, 0, len(li)-1) 41 42 43 li = list(range(16)) 44 random.shuffle(li) 45 print(li) 46 merge_sort(li) 47 48 print(li)
5、归并排序的时间复杂度:O(nlogn),空间复杂度是:O(n)
总结:
LOw B 三人组
- 冒泡排序,选择排序,直接插入排序他们的时间复杂度都是O(n^2),空间复杂度是O(1)
NB 三人组
- 快速排序,归并排序,堆排序他们的时间复杂度都是O(nlogn)
- 三种排序算法的缺点
- 快速排序:极端情况下排序效率低
- 归并排序:需要额外的内存开销
- 堆排序:在快的排序算法中相对较慢
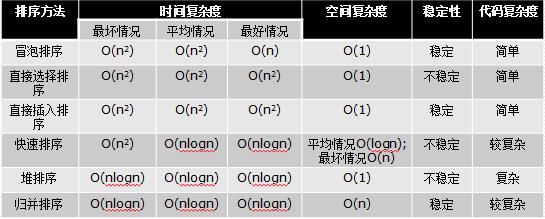
挨着换的稳定,不挨着换的不稳定
