今天闲来无事，考虑到以前都没有好好研究过卷积层、池化层等等的前向/反向传播的原理，所以今天就研究了一下，参考了一篇微信好文，讲解如下：
参考链接：https://www.zybuluo.com/hanbingtao/note/485480
https://github.com/hanbt/learn_dl/blob/master/cnn.py
一、卷积层
（1）首先是卷积神经网络中的卷积操作：
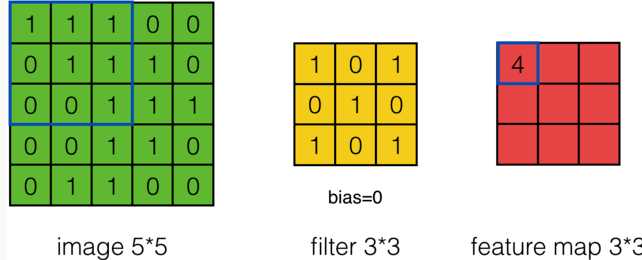
计算公式为：
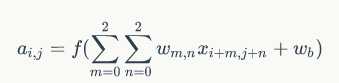
注意上式的使用场景：stride = 1 , channel = 1
我们可以将其扩展到 stride = s , channel = d时的情况，这个时候公式如下：
（2）然后，我们再来看一下数学中的卷积操作，下面引入数学中的二维卷积公式：
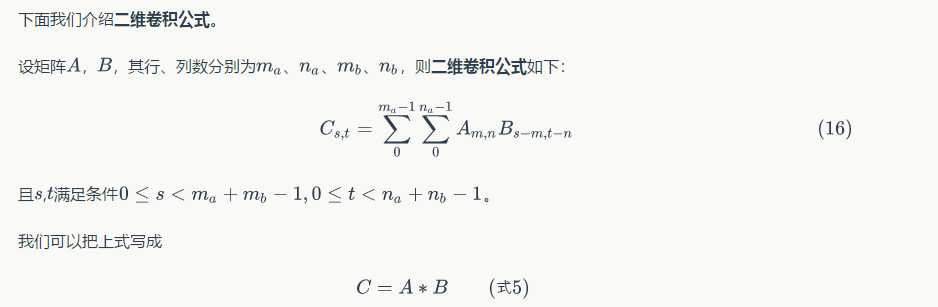
对于如下的图，数学中的卷积操作如下：
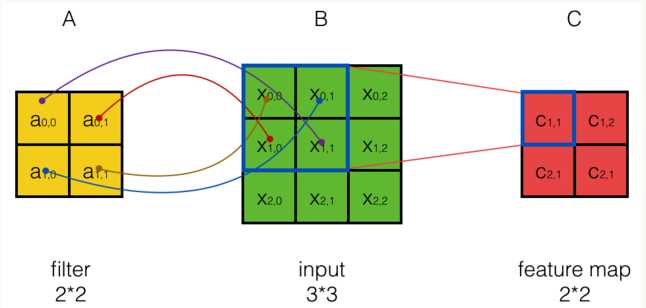
从上图可以看到，A左上角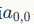
的值与B对应区块中右下角
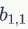的值相乘，而不是与左上角
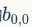的相乘。因此，数学中的卷积和卷积神经网络中的『卷积』还是有区别的，为了避免混淆，我们把卷积神经网络中的『卷积』操作叫做互相关(cross-correlation)操作。
另外：数学卷积和互相关操作是可以相互转化的，比如对于C = A * B，这里A和B的卷积就相当于将B翻转180度然后与A做互相关操作得到。
（3）再来说说卷积层的前向、反向传播：
首先是前向传播：很简单，直接使用互相关的公式计算即可；
然后是反向传播：可以参考我之前作的关于全连接层的反向传播过程，原理公式近似；
具体说一下反向传播过程：
首先引入一道题：
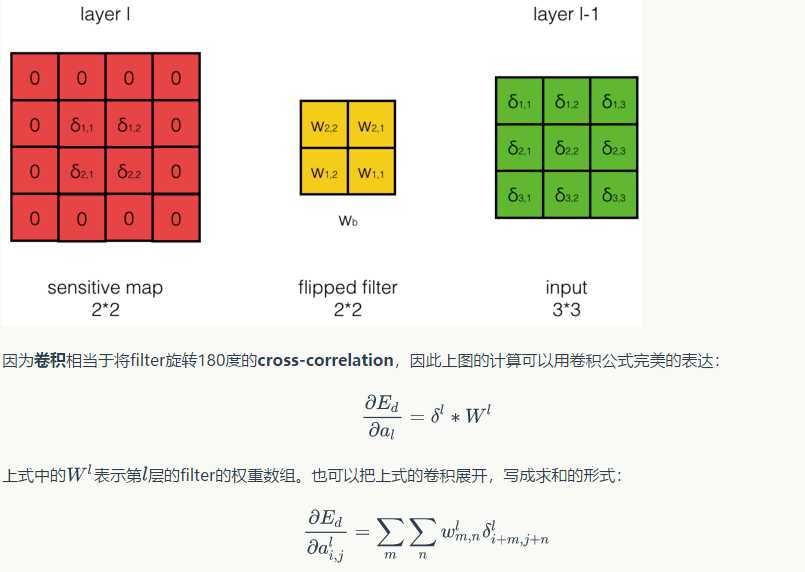
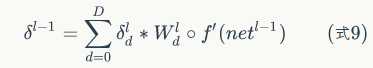
可以发现，卷积层的反向传播过程和全连接层的反向传播过程真的是神似啊，只不过公式需要对应的修改一下；
这里还要注意一点的是，步长stride = s和stride = 1时反向传播的区别：
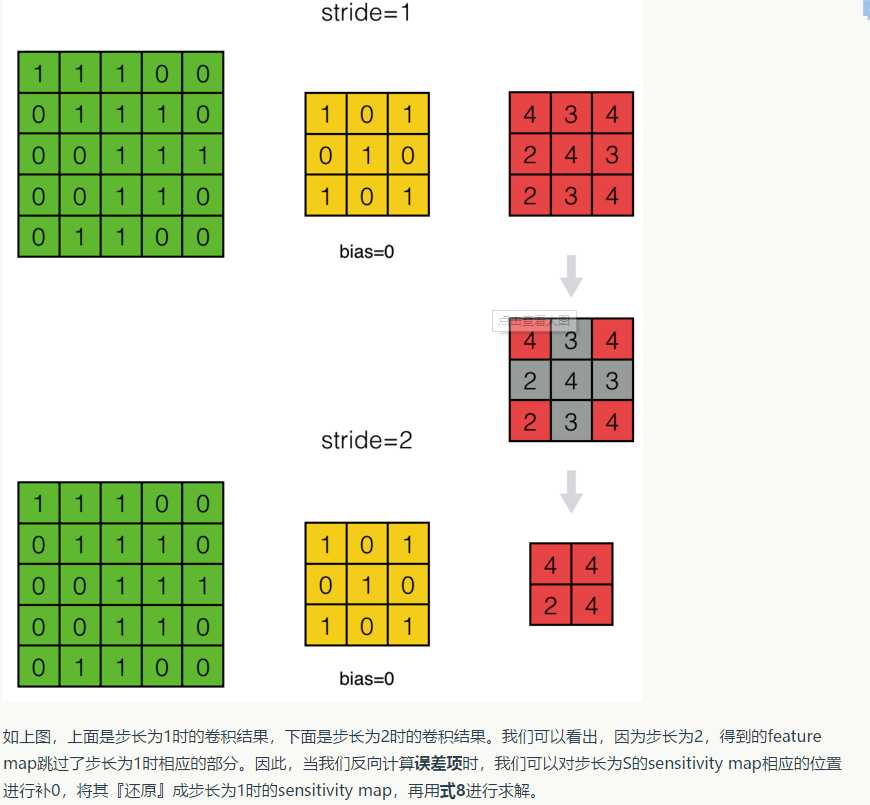
这里面就涉及到了“扩展”和"zero padding"操作，在后面代码中有所体现；
紧接着我们可以得到权重梯度和偏置项梯度如下：
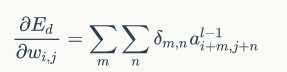
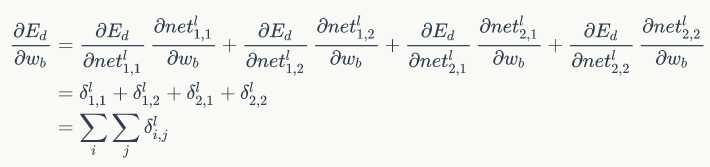
好的，放出代码了，如下：
import numpy as np from activators import ReluActivator , IdentityActivator #获取卷积区域 def get_patch(input_array , i , j , filter_width , filter_height , stride): ‘‘‘ 从输入数组中获取本次卷积的区域，自动适配输入为2D和3D的情况 ‘‘‘ start_i = i * stride start_j = j * stride if input_array.dim == 2: return input_array[start_i : start_i + filter_height , start_j : start_j + filter_width] elif input_array.dim == 3: return input_array[: , start_i : start_i + filter_height , start_j : start_j + filter_width] #获取一个2D区域的最大值的索引 def get_max_index(array): max_i = 0 max_j = 0 max_value = array[0 , 0] for i in range(array.shape[0]): for j in range(array.shape[1]): if(array[i , j] > max_value): max_value = array[i , j] max_i , max_j = i , j return max_i , max_j #计算卷积，是互相关操作 def conv(input_array , kernel_array , output_array , stride , bias): ‘‘‘ 计算卷积，自动适配输入为2D和3D的情况 ‘‘‘ channel_number = input_array.ndim output_width = output_array.shape[1] output_height = output_array.shape[0] kernel_width = kernel_array.shape[1] kernel_height = kernel_array.shape[0] for i in range(output_height): for j in range(output_width): output_array[i][j] = ( get_patch(input_array , i , j , kernel_width , kernel_height , stride) * kernel_array).sum() + bias #对数组增加zero padding def padding(input_array , zp): ‘‘‘ 对数组增加zero padding，自动适配2D的情况 ‘‘‘ if zp == 0: retrun input_array else: if(input_array.ndim == 3): input_width = input_array.shape[2] input_height = input_array.shape[1] input_depth = input_array.shape[0] padded_array = np.zeros((input_depth , input_height + 2 * zp , input_width + 2 * zp)) padded_array[: , zp : zp + input_height , zp : zp + input_width] = input_array return padded_array elif (input_array.ndim == 2): input_width = input_array.shape[1] input_height = input_array.shape[0] padded_array = np.zeros((input_height + 2 * zp , input_width + 2 * zp)) padded_array[zp : zp + input_height , zp : zp + input_width] = input_array return padded_array #对numpy数组进行element wise操作 def element_wise_op(array , op): for i in np.nditer(array , op_flags = [‘readwrite‘]): i[...] = op(i) #卷积核类 class Filter(object): def __init__(self , width , height , depth): self.weights = np.random.uniform(-1e-4 , 1e-4 , (depth , height , width)) self.bias = 0 self.weights_grad = np.zeros(self.weights.shape) self.bias_grad = 0 def __repr__(self): return ‘filter weights : \\n%s\\nbias : \\n%s‘ % (repr(self.weights) , repr(self.bias)) def get_weights(self): return self.weights def get_bias(self): return self.bias def update(self , learning_rate): self.weights -= learning_rate * self.weights_grad self.bias -= learning_rate * self.bias_grad #卷积层类 class ConvLayer(object): def __init__(self , input_width , input_height , channel_number, filter_width , filter_height , filter_number , zero_padding , stride , activator , learning_rate): self.input_width = input_width self.input_height = input_height self.channel_number = channel_number self.filter_width = filter_width self.filter_height = filter_height self.filter_number = filter_number self.zero_padding = zero_padding self.stride = stride self.output_width = ConvLayer.calculate_output_size(self.input_width , filter_width , zero_padding , stride) self.output_height = ConvLayer.calculate_output_size(self.input_height , filter_height , zero_padding , stride) self.output_array = np.zeros((self.filter_number , self.output_height , self.output_width)) self.filters = [] for i in range(filter_number): self.filters.append(Filter(filter_width , filter_height , filter_number)) self.activator = activator self.learning_rate = learning_rate def forward(self , input_array): ‘‘‘ 计算卷积层的输出 输出结果保存在self.output_array ‘‘‘ self.input_array = input_array self.padded_input_array = padding(input_array , self.zero_padding) for f in range(self.filter_number): filter = self.filters[f] conv(self.padded_input_array , filter.get_weights() , self.output_array[f] , self.stride , filter.get_bias()) element_wise_op(self.output_array , self.activator.forward) #对输出的每一个元素做激活操作 def backward(self , input_array , sensitivity_array , activator): ‘‘‘ 计算传递给前一层的误差项，以及计算每个权重的梯度 前一层的误差项保存在self.delta_array，梯度保存在Filter对象的weights_grad中 ‘‘‘ self.forward(input_array) self.bp_sensitivity_map(sensitivity_array , activator) self.bp_gradient(sensitivity_array) def update(self): ‘‘‘ 按照梯度下降，更新权重 ‘‘‘ for filter in self.filters: filter.update(self.learning_rate) #计算传递到上一层的误差项 def bp_sensitivity_map(self , sensitivity_array , activator): ‘‘‘ 计算传递到上一层的sensitivity_map sensitivity_array：本层的sensitivity map activator：上一层的激活函数 ‘‘‘ #处理卷积步长，对原始sensitivity map进行扩展 expanded_array = self.expand_sensitivity_map(sensitivity_array) #full卷积，对sensitivity map进行zero padding #虽然原始输入的zero padding单元也会获得残差，但这个残差不需要继续向上传播，因此就不计算了 expanded_width = expanded_array.shape[2] #zero padding的值 zp = (self.input_width + self.filter_width - 1 - expanded_width) / 2 padded_array = padding(expanded_array , zp) #初始化delta_array,用于保存传递到上一层的sensitivity map self.delta_array = self.create_delta_array() #对于具有多个filter的卷积层来说，最终传递到上一层的sensitivity map相当于所有filter的sensitivity map之和 #注意：这里的求和只是针对所有的num求和，而不是针对所有的channel求和； for f in range(self.filter_number): filter = self.filters[f] #将filter的权重翻转180度 filpped_weights = np.array(map(lambda i : np.rot90(i , 2) , filter.get_weights())) #计算与一个filter对应的delta_array delta_array = self.create_delta_array() for d in range(delta_array.shape[0]): conv(padded_array[f] , filpped_weights[d] , delta_array[d] , 1 , 0) self.delta_array += delta_array #将计算结果与激活函数的偏导数做element-wise惩罚操作 derivative_array = np.array(self.input_array) element_wise_op(derivative_array , activator.backward) self.delta_array *= derivative_array #计算传递到上一层的权重梯度 def bp_gradient(self , sensitivity_array): #处理卷积步长，对原始的sensitivity map进行扩展 expanded_array = self.expand_sensitivity_map(sensitivity_array) for f in range(self.filter_number): #计算每个权重的梯度 filter = self.filters[f] for d in range(filter.weights.shape[0]): conv(self.padded_input_array[d] , expanded_array[f] , filter.weights_grad[d] , 1 , 0) #计算偏置项的梯度 filter.bias_grad = expanded_array[f].sum() #对步长不为1的sensitivity map进行扩展，使之还原成stride=1时的情况 def expand_sensitivity_map(self , sensitivity_array): depth = sensitivity_array.shape[0] #确定扩展后sensitivity map的大小 #计算stride为1时的sensitivity map的大小，之所以这么做是因为后面对于stride不等于1的情况时，进行反向传播时，都是先还原成stride=1时的情况再做处理 expanded_width = (self.input_width - self.filter_width + 2 * zero_padding + 1) expanded_height = (self.input_height - self.filter_height + 2 * zero_padding + 1) #构建新的sensitivity map expand_array = np.zeros((depth , expanded_height , expanded_width)) #从原始的sensitivity map拷贝误差值 for i in range(self.output_height): for j in range(self.output_width): i_pos = i * self.stride j_pos = j * self.stride expand_array[: , i_pos , j_pos] = sensitivity_array[: , i , j] #stride = s还原到stride=1时的情况，通过对应位置0进行扩展 return expand_array def create_delta_array(self): return np.zeros((self.channel_number , self.input_height , self.input_width)) @staticmethod def calculate_output_size(input_size , filter_size , zero_padding , stride): return (input_size - filter_size + 2 * zero_padding) / stride + 1
二、池化层