KMP算法-从入门到进阶

Posted 2020-10-28 葡萄美酒夜光杯

题目描述

给定一个文本串text和模式串pattern，从文本串中找出模式串第一次出现的位置

先来看最简单的方法，方便理解题目，也就是暴力求解

暴力求解

放大上面的图，得到下面这个。题目要求匹配到整个字符串，从开始匹配考虑。

用模式串的首元素去匹配文本串的每一个元素，如果能匹配到，则依次向后匹配，直到所有的模式串匹配成功。

如果模式串中有一个不匹配，则pattern回到首元素匹配test中的下一元素。

这里需要注意的是，模式串首元素需要匹配的最后一个元素是text-j，因为如果匹配到最后，模式串比text长是没有意义的。

整个流程，可以想象是先把模式串与text对齐，然后相对于text依次后移一位，拖动pattern，每次移动都比较整个pattern模式串每个元素（理解这个有助于后面分析）

关键代码如下

int search(const char*s, const char*p)
{
    int i = 0;//用于标记匹配到text字符串的位置
    int j = 0;//标记模式串中匹配的位置
    int size = (int)strlen(p);
    int nLast = (int)strlen(s) - size; //此处为匹配到text中最长位置
    while((i <=  nLast) && (j < size))
    {
        if (s[i+j] == p[j])
        {
            j ++;
        }
        else{
            i++;
            j = 0; //j回到模式串首元素
        }
    }
    if(j >= size)
        return i;
    return -1;
}

记text长度为N，pattern长度为M。在这个方法中，时间复杂程度为O(M*N)，空间复杂程度为O(1)

进一步分析：

在暴力求解中，为什么模式串的索引 j 会回溯？原因是模式串需要依次匹配整个才能知道是否完全匹配。

所以，增加一个条件，如果模式串的字符两两不相等。也就意味着模式串只要一次不匹配，整个 j 的长度都不会匹配上，就可以向后拖动pattern到自身长度的位置。

即，如果发生了不匹配，则向后移动 i+j 个位置开始匹配。

现在整个算法的时间复杂度退化成了O(N)，但这是在模式串两两不等的情况下才有的结论。那这个条件可以弱化吗？

当然是可以，弱化后条件变为：模式串首字符和其他字符不相等。

继续分析：

在上图中P和D是刚好不匹配的一个元素。为了让pattern能尽可能多的往后拖动，那么拖动到一个什么样的位置是合适的呢？

如果说拖动到一个C与P开始比较的位置，那么意味着A==Q。因为只有事先知道Q==A，才能进行P与C的比较。这次拖动的上一步中P!=D匹配失败，B也刚与Q匹配完，B==Q。所以由此推出B和A是相等的。

通过上面的分析，已经得到了一个拖动模式串的规则。下面继续分析如何提前找到A==B

求解next数组

定义：如上字符串中，A为D的前缀串，B为D的后缀串。A==B且是最长串，这个最长串组成的数据即为next数组。下面列表举例：

pattern	a	b	a	a	b	c	a	b	a
next	-1	0	0	1	1	2	0	1	2

pattern的每个元素的next值，代表它前面的字符串，前缀后缀最长匹配长度。这个next数组表示就是pattern最远能滑动到的位置

那么如何求这个数组呢？下面分析next数组的递推关系：

next[j]=k，则对于模式串的位置j+1，考察Pj：

若p[k]=p[j]：则next[j+1]=next[j]+1

这个好理解，j+1的最长匹配的前后串就是在原来的基础上增加了一个 k==j 元素

若p[k]!=p[j]：则记h=next[k]；如果p[h]==p[j]，则next[j+1]=h+1，否则重复此过程

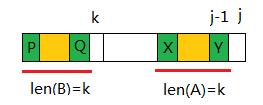
对于元素k来说，next[k]是k前面的字符串最长匹配长度，同时B和A是已经匹配的串。那么P==Q==X==Y。p[h]是P字段后面的一个元素，如果p[h]==p[j]，就是P字段加上p[h]与Y字段加上p[j]匹配。故next(j+1)=h+1

参考代码片段如下：

void GetNext(char *p, int next[])
{
	int nLen = (int)strlen(p);
	next[0] = -1;
	int k = -1;
	int j = 0;
	while (j < nLen - 1)
	{
		//这里,k表示next[j-1],且p[k]表示前缀,p[j]表示后缀
		//注:k==-1表示未找到k前缀与k后缀相等,首次分析可先忽略
		if (k == -1 || p[j] = p[k])
		{
			++j;
			++k;
			next[j] = k; //已经做了++j计算,此处不写j+1
		}else{ //p[j]与p[k]不匹配,继续递归计算前缀p[next[k]]
			k = next[k];
		}
	}
}

　　

int KMP(int n)
{
	int ans = -1;
	int i = 0;
	int j = 0;
	int pattern_len = strlen(g_pattern);
	while(i < n)
	{
		if(j == -1 || g_s[i] == g_pattern[j])
		{
			++i; ++j;
		}else
			j = g_next[j]
		if(j == pattern_len)
		{
			ans = i - pattern_len;
			break;
		}
	}
	return ans;
}