luogu 3415 祭坛

Posted 2020-10-28 jack_yyc

题目大意：

Dgeak大陆可以看成一个用平面直角坐标系表示的巨大平面。在这个平面上，有 n 个Swaryea水晶柱，每个水晶柱可以用一个点表示。

如果 4 个水晶柱依次相连可以构成一个四边形，满足其两条对角线分别平行于 x 轴和 y 轴，并且对角线的交点位于四边形内部（不包括边界），那么这 4 个水晶柱就可以建立一个结界。其中，对角线的交点称作这个结界的中心。

例如下左图中，水晶柱 ABCD 可以建立一个结界，其中心为 O。

 

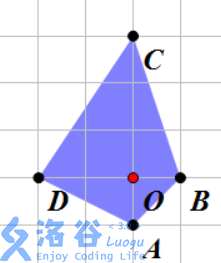
为了起到抵御Dar-dzo-nye的最佳效果，人们会把祭坛修建在最多层结界的保护中。其中不同层的结界必须有共同的中心，这些结界的边界不能有任何公共点，并且中心处也不能有水晶柱。这里共同中心的结界数量叫做结界的层数。

为了达成这个目的，人们要先利用现有的水晶柱建立若干个结界，然后在某些结界的中心建立祭坛。

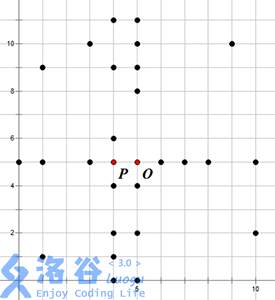
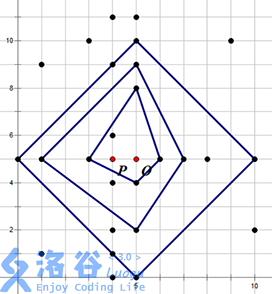
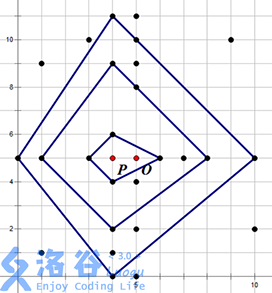
例如上右图中，黑色的点表示水晶柱（注意 P 和 O 点不是水晶柱）。祭坛的一个最佳位置为 O 点，可以建立在 3 层结界中，其结界的具体方案见下左图。当然，建立祭坛的最佳位置不一定是唯一，在上右图中，O 点左侧 1 单位的点 P 也可以建立一个在 3 层结界中的祭坛，见下右图。

 

现在人们想知道：

1. 祭坛最佳选址地点所在的结界层数；

2. 祭坛最佳的选址地点共有多少个

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cmath>
 4 #include<cstdlib>
 5 #include<cstring>
 6 #include<algorithm>
 7 #include<vector>
 8 #include<queue>
 9 #define inf 2139062143
10 #define ll long long
11 #define MAXN 100100
12 using namespace std;
13 inline int read()
14 {
15     int x=0,f=1;char ch=getchar();
16     while(!isdigit(ch)) {if(ch==‘-‘) f=-1;ch=getchar();}
17     while(isdigit(ch)) {x=x*10+ch-‘0‘;ch=getchar();}
18     return x*f;    
19 }
20 int n,up[MAXN],dn[MAXN],q[MAXN],cnt;
21 vector<int> vec[MAXN];
22 int c[MAXN],shu[MAXN];
23 int lowbit(int x) {return x&(-x);}
24 void add(int x,int val) {for(int i=x;i<=n;i+=lowbit(i)) c[i]+=val;}
25 int query(int x) {int res=0;for(int i=x;i;i-=lowbit(i)) res+=c[i];return res;}
26 int check(int x)
27 {
28     int res=0;
29     memset(shu,0,sizeof(shu)),memset(c,0,sizeof(c));
30     memset(dn,0,sizeof(dn)),memset(up,0,sizeof(up));
31     for(int i=1;i<=cnt;i++)
32         for(int j=vec[q[i]].size()-1;j>=0;j--) dn[vec[q[i]][j]]++;
33     for(int k=1;k<=cnt;k++)
34     {
35         int t=q[k];
36         for(int i=vec[t].size()-1;i>=0;i--)
37         {
38             dn[vec[t][i]]--;
39             if((dn[vec[t][i]]<x||up[vec[t][i]]<x)&&shu[vec[t][i]])
40                 shu[vec[t][i]]=0,add(vec[t][i],-1);
41         }
42         if(x-1<vec[t].size())
43         {
44             int l=vec[t][x-1],r=vec[t].size()-x;
45             if(r<0) goto ed;
46             r=vec[t][r];
47             if(r>0&&l<=r-1) res+=query(r-1)-query(l);
48         }ed:;
49         for(int i=vec[t].size()-1;i>=0;i--)
50         {
51             up[vec[t][i]]++;
52             if(dn[vec[t][i]]>=x&&up[vec[t][i]]>=x&&!shu[vec[t][i]]) {shu[vec[t][i]]=1,add(vec[t][i],1);}
53         }
54     }
55     return res;
56 }
57 int main()
58 {
59     n=read();int a,b;
60     for(int i=1;i<=n;i++)
61     {
62         a=read(),b=read();
63         vec[a].push_back(b);
64         q[++cnt]=a;
65     }
66     sort(q+1,q+cnt+1);
67     cnt=unique(q+1,q+cnt+1)-q-1;
68     for(int i=1;i<=cnt;i++) sort(vec[q[i]].begin(),vec[q[i]].end());
69     int l=1,r=n,ans=0,res=0;
70     while(l<=r)
71     {
72         int mid=l+r>>1;
73         if(a=check(mid)) ans=mid,l=mid+1,res=a;
74         else r=mid-1;
75     }
76     printf("%d\n%d",ans,res);
77 }

View Code