主成分分析法就是通过正交变换将存在相关性的原始变量变量转换成不相关的新变量,将其中贡献度低的变量舍弃掉,贡献度可以理解为变量的方差,方差越大,贡献度越高,正交变换前后变量存在的信息量是相同的,只是把更多的信息集中起来,舍弃存在少量信息的变量,达到降维的目的。
运用主成分的前提是变量之间存在相关性
主成分分析法的实质的正交变换,正交变换实质就是矩阵的对角化,使得协方差矩阵为对角矩阵,各个变量之间的相关性为0。
如何确定主成分数量,累计贡献度达到90%左右
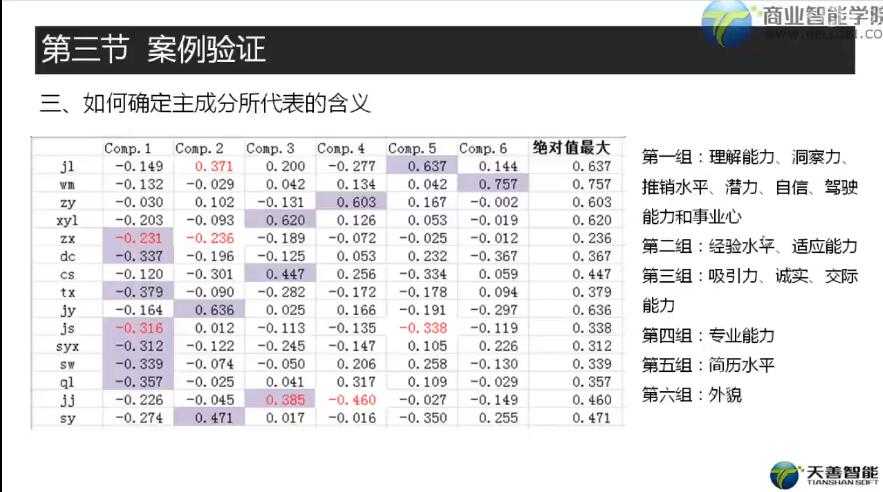
如何确定主成分所代表的的含义:通过找到荷载矩阵每一行的绝对值最大值,例如下图
小结
