本周学习的代码（数构 深度 广度 优先遍历）

Posted 2020-07-08

深度优先遍历代码：

 

#include "stdafx.h"

#include <stdio.h>

#include <string.h>

#define MVNum 100          //最大顶点数 

typedef int InfoType;              //边的权值类型

typedef char*  VexType;          //顶点数据类型

typedef struct LinkNode{     //边结点 

    int adjvex;          //该边所指向的顶点的位置 

    struct LinkNode * next;   //指向下一条边的指针 

    InfoType info;       //和边相关的信息 

}LinkNode; 

typedef struct VexNode{ 

    VexType data;                 //顶点信息 

    LinkNode * firstadj;       //指向第一条依附该顶点的边的指针 

}VexNode ; // VexNode 表示邻接表类型 

typedef struct{ 

    VexNode adjlist[MVNum];        //邻接表 

    int vexnum, arcnum;        //图的当前顶点数和边数

} AdjList;//,AdjGraph;

 

int visited[MVNum];//初始为零，表示此顶点尚未访问

void DFS(AdjList *pg,int i){

int j;

   visited[i]=1;//设置顶点已访问标志

   printf("%s ",pg->adjlist[i].data);//输出顶点数据

   LinkNode *pnode=pg->adjlist[i].firstadj;//取该顶点的连接的边

   while(pnode!=NULL) 

   {   j=pnode->adjvex;//取该顶点相邻的顶点

       pnode=pnode->next;//取该顶点的下一个连接的边

   if(visited[j]==1)//该顶点是否已访问

    continue;//已访问

   DFS(pg,j);//未访问，递归调用访问其邻接顶点

   }

}

int main(int argc, char* argv[])
{ printf(" 邻接表存储结构的深度优先搜索算法\\n");
AdjList ag; //无向图
ag.vexnum=9;
ag.adjlist[0].data="V0";
ag.adjlist[1].data="V1"; ag.adjlist[2].data="V2";
ag.adjlist[3].data="V3"; ag.adjlist[4].data="V4";
ag.adjlist[5].data="V5"; ag.adjlist[6].data="V6";
ag.adjlist[7].data="V7"; ag.adjlist[8].data="V8";
int v0=0,v1=1,v2=2,v3=3,v4=4,v5=5,v6=6,v7=7,v8=8;
LinkNode v12={v2,NULL},v21={v1,NULL}, v13={v3,NULL},v31={v1,NULL},
v24={v4,NULL},v42={v2,NULL},v25={v5,NULL},v52={v2,NULL},
v37={v7,NULL},v73={v3,NULL},v36={v6,NULL},v63={v3,NULL},
v48={v8,NULL},v84={v4,NULL},v58={v8,NULL},v85={v5,NULL},
v67={v7,NULL},v76={v6,NULL};
ag.adjlist[v0].firstadj=NULL; ag.adjlist[v1].firstadj=&v12;
ag.adjlist[v2].firstadj=&v21; ag.adjlist[v3].firstadj=&v31;
ag.adjlist[v4].firstadj=&v42; ag.adjlist[v5].firstadj=&v52;
ag.adjlist[v6].firstadj=&v63; ag.adjlist[v7].firstadj=&v73;
ag.adjlist[v8].firstadj=&v84;
v12.next=&v13;
v21.next=&v24; v24.next=&v25;
v31.next=&v36; v36.next=&v37;
v42.next=&v48; v52.next=&v58;
v63.next=&v67; v73.next=&v76;
v84.next=&v85;
BFSTraverse(&ag,4); // DFSTraverse(&ag,4);

AdjList ag2; //有向图
ag2.vexnum=9;
ag2.adjlist[0].data="V0";
ag2.adjlist[1].data="V1"; ag2.adjlist[2].data="V2";
ag2.adjlist[3].data="V3"; ag2.adjlist[4].data="V4";
ag2.adjlist[5].data="V5"; ag2.adjlist[6].data="V6";
ag2.adjlist[7].data="V7"; ag2.adjlist[8].data="V8";
LinkNode vv12={v2,NULL} ,vv13={v3,NULL}, vv24={v4,NULL}, vv36={v6,NULL},
vv48={v8,NULL}, vv67={v7,NULL}, vv85={v5,NULL};
ag2.adjlist[v0].firstadj=NULL;
ag2.adjlist[v1].firstadj=&vv12; ag2.adjlist[v2].firstadj=&vv24;
ag2.adjlist[v3].firstadj=&vv36; ag2.adjlist[v4].firstadj=&vv48;
ag2.adjlist[v5].firstadj=NULL; ag2.adjlist[v6].firstadj=&vv67;
ag2.adjlist[v7].firstadj=NULL; ag2.adjlist[v8].firstadj=&vv85;
vv12.next=&vv13;
BFSTraverse(&ag2,4);//DFSTraverse(&ag2,4);
return 0;
}

 

void DFSTraverse(AdjList *pg,int k){ //从第k个顶点开始遍历

    int i;

for(i=0;i<pg->vexnum;i++)

 visited[i]=0; //初始设置每个顶点尚未访问

i=k;

while(1){

  if( visited[i]==0)  //第i个顶点已访问否

    DFS(pg,i); //未访问，则访问此顶点

    i++;     //访问下一个顶点   

if(i>=pg->vexnum)  //到达数组尾部,则从零开始，继续访问

{ i=0;

}

 if(i==k) break;  //回到原来顶点位置，则访问结束

}

   printf("\\n");

}

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

广度优先遍历代码：

// Graph广度_邻接表.cpp : Defines the entry point for the console application.

//

 

#include "stdafx.h"

 

#include "stdafx.h"

#include <stdio.h>

#define MVNum 100          //最大顶点数 

typedef int InfoType;              //边的权值类型

typedef char* VexType;          //顶点数据类型

//#define char[10] VexType;       //顶点数据类型

typedef struct LinkNode{     //边结点 

    int adjvex;          //该边所指向的顶点的位置 

    struct LinkNode * next;   //指向下一条边的指针 

    InfoType info;       //和边相关的信息 

}LinkNode; 

typedef struct VexNode{ 

    VexType data;                 //顶点信息 

    LinkNode * firstadj;       //指向第一条依附该顶点的边的指针 

}VexNode ; // VexNode 表示邻接表类型 

typedef struct{ 

    VexNode adjlist[MVNum];        //邻接表 

    int vexnum, arcnum;        //图的当前顶点数和边数

} AdjList;//,AdjGraph;

/****************************************/

#define MAX_QUEUE MVNum        /* 队列的最大数据元素数目 */

typedef  int  Elemtype;

typedef struct queue             /* 假设当数组只剩下一个单元时认为队满 */

{

    Elemtype elem[MAX_QUEUE];  /* 存放队列中数据元素的存储单元 */

    int front,rear;                  /* 队头指针、队尾指针 */

}QUEUE;

//1）初始化队列Q

void InitQueue(QUEUE *Q)

{ Q->front=0;

  Q->rear=0;

}

//5）判断队列Q是否为空

int QueueEmpty(QUEUE Q)

{

    if(Q.front==Q.rear) return 1;//头指针相同，表示队列为空

    else return 0;

}

//2）入队

void EnQueue(QUEUE *Q,Elemtype elem)

{ if((Q->rear+1)%MAX_QUEUE==Q->front)//判断队列是否已满，

       printf("Queue is full.\\n");// 已满，则不能入队，推出

  else { Q->elem[Q->rear]=elem; //未满，数据入队

     Q->rear=(Q->rear+1)%MAX_QUEUE; //队尾指针加一

          

  }

}

//3）出队

Elemtype DeQueue(QUEUE*Q)

{   Elemtype e=-1;

if(QueueEmpty(*Q)) printf("Queue is empty.\\n");//队列为空，不能出对，

    else 

    {

        e=Q->elem[Q->front]; //队列不为空，要删除的数据保存到elem

Q->front=(Q->front+1)%MAX_QUEUE;//队头针加一

    }

return e;

}

int visited[MVNum];

void BFS(AdjList *pg,int i){

int j,k;

QUEUE q;

   InitQueue(&q);//初始化队列

   visited[i]=1;//设置此顶点已被访问

   printf("%s ",pg->adjlist[i].data);//输出此顶点数据

   EnQueue(&q,i);//此顶点入对

   LinkNode *pnode;

   while(!QueueEmpty(q)){//队列为空则结束

   k=DeQueue(&q); //顶点数据出对

       pnode=pg->adjlist[k].firstadj;//获取此顶点的边

       while(pnode!=NULL) 

   {   j=pnode->adjvex;//获取当前顶点的相邻顶点

       if(visited[j]==0) //此相邻顶点已访问否

   { visited[j]=1; //未访问，置为已访问

             printf("%s ",pg->adjlist[j]);//输出相邻顶点的数据

     EnQueue(&q,j);//相邻顶点入队

   }

            pnode=pnode->next;//获取与当前顶点连接的边

   }

   } 

}

 

void BFSTraverse(AdjList *pg,int k){//从第K个顶点开始访问

    int i;

for(i=0;i<pg->vexnum;i++)

 visited[i]=0;//初始设置每个顶点尚未访问

i=k;

while(1){

  if( visited[i]==0)//第i个顶点已访问否

    BFS(pg,i);//未访问，则访问此顶点

    i++;//访问下一个顶点       

if(i>=pg->vexnum) //到达数组尾部,则从零开始，继续访问

{

i=0;

}

 if(i==k) break; //回到原来顶点位置，则访问结束

}

    printf("\\n");

}

int main(int argc, char* argv[])
{ printf("邻接表存储结构的广度优先搜索算法\\n");
AdjList ag; //无向图
ag.vexnum=9;
ag.adjlist[0].data="V0";
ag.adjlist[1].data="V1"; ag.adjlist[2].data="V2";
ag.adjlist[3].data="V3"; ag.adjlist[4].data="V4";
ag.adjlist[5].data="V5"; ag.adjlist[6].data="V6";
ag.adjlist[7].data="V7"; ag.adjlist[8].data="V8";
int v0=0,v1=1,v2=2,v3=3,v4=4,v5=5,v6=6,v7=7,v8=8;
LinkNode v12={v2,NULL},v21={v1,NULL}, v13={v3,NULL},v31={v1,NULL},
v24={v4,NULL},v42={v2,NULL},v25={v5,NULL},v52={v2,NULL},
v37={v7,NULL},v73={v3,NULL},v36={v6,NULL},v63={v3,NULL},
v48={v8,NULL},v84={v4,NULL},v58={v8,NULL},v85={v5,NULL},
v67={v7,NULL},v76={v6,NULL};
ag.adjlist[v0].firstadj=NULL; ag.adjlist[v1].firstadj=&v12;
ag.adjlist[v2].firstadj=&v21; ag.adjlist[v3].firstadj=&v31;
ag.adjlist[v4].firstadj=&v42; ag.adjlist[v5].firstadj=&v52;
ag.adjlist[v6].firstadj=&v63; ag.adjlist[v7].firstadj=&v73;
ag.adjlist[v8].firstadj=&v84;
v12.next=&v13;
v21.next=&v24; v24.next=&v25;
v31.next=&v36; v36.next=&v37;
v42.next=&v48; v52.next=&v58;
v63.next=&v67; v73.next=&v76;
v84.next=&v85;
DFSTraverse(&ag,4); // DFSTraverse(&ag,4);

AdjList ag2; //有向图
ag2.vexnum=9;
ag2.adjlist[0].data="V0";
ag2.adjlist[1].data="V1"; ag2.adjlist[2].data="V2";
ag2.adjlist[3].data="V3"; ag2.adjlist[4].data="V4";
ag2.adjlist[5].data="V5"; ag2.adjlist[6].data="V6";
ag2.adjlist[7].data="V7"; ag2.adjlist[8].data="V8";
LinkNode vv12={v2,NULL} ,vv13={v3,NULL}, vv24={v4,NULL}, vv36={v6,NULL},
vv48={v8,NULL}, vv67={v7,NULL}, vv85={v5,NULL};
ag2.adjlist[v0].firstadj=NULL;
ag2.adjlist[v1].firstadj=&vv12; ag2.adjlist[v2].firstadj=&vv24;
ag2.adjlist[v3].firstadj=&vv36; ag2.adjlist[v4].firstadj=&vv48;
ag2.adjlist[v5].firstadj=NULL; ag2.adjlist[v6].firstadj=&vv67;
ag2.adjlist[v7].firstadj=NULL; ag2.adjlist[v8].firstadj=&vv85;
vv12.next=&vv13;
DFSTraverse(&ag2,4);//DFSTraverse(&ag2,4);
return 0;
}

 

 

 

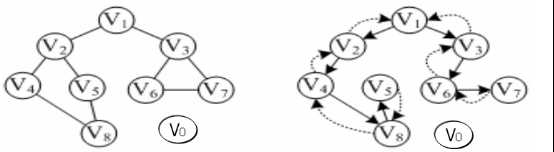
实在不得不说有时候真的会给代码弄晕，指来指去，今天上机课硬是没打代码打完整