Dijkstra算法图解
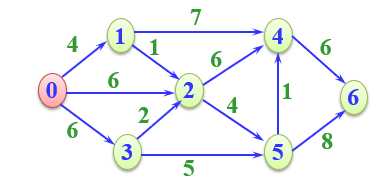
说明:
初始化:S = { 0 }, U = { 1, 2, 3, 4, 5, 6 }, dist[ ] = { 0, 4, 6, 6, ∞, ∞ }, path[ ] = { 0, 0, 0, 0, -1, -1, -1 }
第一步:从U中找到最小的顶点1,将它添加到S中,S ={ 0, 1 }, 考查顶点1, 发现顶点1到顶点2和4有边:
dist[ 2 ] = MIN{dist[ 2 ], dist[ 1 ] +1 } = 5(修改)
dist[ 4 ] = MIN{dist[ 4 ], dist[ 1 ] +7 } = 11(修改)
则S ={ 0, 1 },dist[ ] = { 0, 4, 5, 6, 11, ∞ },path[ ] = { 0, 0, 1, 0, 1, -1, -1 }.
第二步:从U中找到最小的顶点2,将它添加到S中,S ={ 0, 1,2 }, 考查顶点2, 发现顶点2到顶点4和5有边:
dist[ 4 ] = MIN{dist[ 2 ], dist[ 2 ] +6 } = 11
dist[ 5 ] = MIN{dist[ 4 ], dist[ 2 ] +4 } = 9(修改)
则S ={ 0, 1,2 },dist[ ] = { 0, 4, 5, 6, 11, 9 },path[ ] = { 0, 0, 1, 0, 1, 2, -1 }.
第三步:从U中找到最小的顶点3,将它添加到S中,S ={ 0, 1,2, 3 }, 考查顶点3, 发现顶点3到顶点2和5有边, 由于顶点2已经考察过,不进行修改:
dist[ 5 ] = MIN{dist[ 5 ], dist[ 3 ] +5 } = 9
则S ={ 0, 1,2, 3},dist[ ] = { 0, 4, 5, 6, 9, ∞ },path[ ] = { 0, 0, 1, 0, 1, 2, -1 }.
第四步:从U中找到最小的顶点5,将它添加到S中,S ={ 0, 1,2, 3, 5 }, 考查顶点5, 发现顶点3到顶点4和6有边:
dist[ 4 ] = MIN{dist[ 4 ], dist[ 5 ] +1 } = 10(修改)
dist[ 6 ] = MIN{dist[ 6 ], dist[ 5 ] +8 } = 11(修改)
则S ={ 0, 1,2, 3, 5},dist[ ] = { 0, 4, 5, 5, 9, ∞ },path[ ] = { 0, 0, 1, 0, 5, 2, 5 }.