dsu on tree
Posted 人活着就是为了Chelly
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了dsu on tree相关的知识,希望对你有一定的参考价值。
开头致敬原文:http://codeforces.com/blog/entry/44351
dsu on tree 是一个很神奇的技术,可以替代启发式合并、点分治,可以处理无修改的子树询问问题,可以处理任何乱搞的询问,是“树上的莫队”。
一、什么是dsu on tree
从一个例题看起:现在有一个树,每个点都有一个颜色,现在对于以每个点为根的子树我们需要回答问题,即这个子树里出现次数最多的颜色的数值和。(假设颜色3和颜色5都出现4次且是最多,那么答案就是3+5)。这个是在树上询问,但是询问的东西很奇怪,应该不能有现成的一些数据结构来处理它,这种乱搞的询问很容易让人想到莫队。
做法一:
我们对这个树进行dfs序,然后子树询问就变成了区间询问,直接莫队就行了,时间复杂度O(nsqrt(n))
做法二:
我们考虑以下一种暴力的做法。
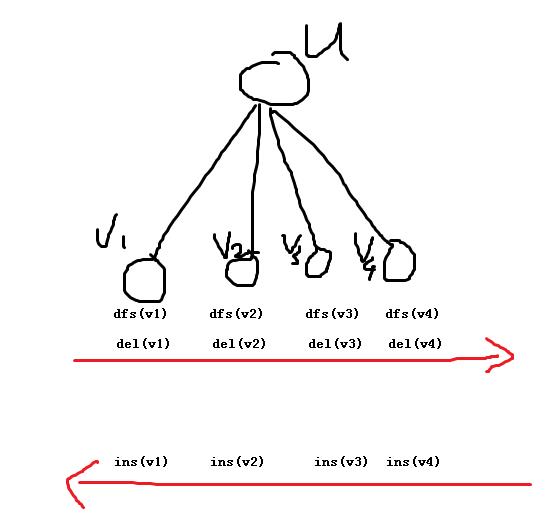
对于处理以u为根的子树的答案,我们先去dfs其所有孩子,先处理完这些子树的答案,dfs完v1之后记得把v1子树里的所有信息都从全局数组中删除(为了不对dfs(v2)造成影响)
然后我们要去统计u点的答案,我们只需要把所有v的子树里的信息全部加入全局数组,就能计算出u点答案了
这个暴力显然是O(n^2)的
做法三:
我们发现在做法二的暴力里面,有个小小的地方是可以优化的,那就是对于v4,dfs(v4)结束后,我们没必要del(v4),因为v4的信息我在统计u的答案的时候要用到
于是我们自然就希望v4是所有v中size最大的
其实这个小优化就是dsu on tree了,即对树进行轻重边剖分,得到每个点的重儿子,把重儿子放最后,省去del(重儿子)这一步骤
我们来分析一下这个的复杂度
每个点被加入全局数组当且仅当是轻边被合并到重链上,而重链个数只有logn个,所以每个点都被加入全局数组logn次,所以时间复杂度是O(nlogn)的!!!
二、dsu on tree相关例题
1、codeforces 600E
题意:
就是第一部分讲的例题
分析:
模板题了

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int maxn=1e5; 5 int c[maxn+5],l[maxn+5],r[maxn+5],dfn[maxn+5],son[maxn+5],sz[maxn+5]; 6 ll cnt[maxn+5],sum[maxn+5]; 7 ll mx; 8 ll ans[maxn+5]; 9 int n,dfstime; 10 vector<int> g[maxn+5]; 11 void pre(int k,int fa) 12 { 13 sz[k]=1; 14 l[k]=++dfstime; 15 dfn[dfstime]=k; 16 for(auto u:g[k]) 17 { 18 if(u==fa) continue; 19 pre(u,k); 20 if(sz[u]>sz[son[k]]) son[k]=u; 21 sz[k]+=sz[u]; 22 } 23 r[k]=dfstime; 24 } 25 void del(int k) 26 { 27 for(int i=l[k];i<=r[k];++i) 28 { 29 int u=c[dfn[i]]; 30 sum[cnt[u]]-=u; 31 --cnt[u]; 32 sum[cnt[u]]+=u; 33 if(sum[mx]==0) --mx; 34 } 35 } 36 void ins(int k) 37 { 38 for(int i=l[k];i<=r[k];++i) 39 { 40 int u=c[dfn[i]]; 41 sum[cnt[u]]-=u; 42 ++cnt[u]; 43 sum[cnt[u]]+=u; 44 mx=max(mx,cnt[u]); 45 } 46 } 47 void dfs(int k,int fa) 48 { 49 mx=0; 50 for(auto u:g[k]) 51 { 52 if(u==fa||u==son[k]) continue; 53 dfs(u,k); 54 del(u); 55 } 56 if(son[k]) dfs(son[k],k); 57 for(auto u:g[k]) 58 { 59 if(u==fa||u==son[k]) continue; 60 ins(u); 61 } 62 int color=c[k]; 63 sum[cnt[color]]-=color; 64 ++cnt[color]; 65 sum[cnt[color]]+=color; 66 mx=max(mx,cnt[color]); 67 ans[k]=sum[mx]; 68 } 69 int main() 70 { 71 scanf("%d",&n); 72 for(int i=1;i<=n;++i) scanf("%d",&c[i]); 73 for(int i=1;i<n;++i) 74 { 75 int x,y; 76 scanf("%d%d",&x,&y); 77 g[x].push_back(y),g[y].push_back(x); 78 } 79 pre(1,0); 80 dfs(1,0); 81 for(int i=1;i<=n;++i) printf("%lld ",ans[i]);printf("\\n"); 82 return 0; 83 }
2、codeforces 741D
题意:
有一个n个点的树,树边上写有一个英文字母,范围是a~v,我们需要统计每个子树里最长的回文路径。回文路径指的是一个简单路径,把这个简单路径上的字符重新排列可以得到一个回文串。
n<=5e5
分析:
考虑状态压缩,把字母压成二进制位,然后回文路径就是路径上的权值异或和要么是0,要么是2的次幂
如果考虑启发式合并,用map记录下每个点的子树里的<权值,该权值对应点的最深深度>,然后不断的把兄弟子树并过去并统计答案就行了
这样复杂度是O(22nlog^2n)的,会TLE
我们可以用dsu on tree代替启发式合并,用全局数组的统计来代替map,这样会少掉一个log(因为这里恰好是22个字符,2^22的数组是空间允许的)

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=5e5; 4 vector<int> g[maxn+5]; 5 int val[maxn+5],dep[maxn+5],ans[maxn+5]; 6 int l[maxn+5],r[maxn+5],son[maxn+5],sz[maxn+5],dfn[maxn+5]; 7 int f[1<<22]; 8 int dfstime; 9 int n; 10 map<int,int> s[maxn+5]; 11 int bin[23]; 12 void pre(int k,int fa) 13 { 14 dep[k]=dep[fa]+1; 15 val[k]^=val[fa]; 16 l[k]=++dfstime; 17 dfn[dfstime]=k; 18 sz[k]=1; 19 for(auto u:g[k]) 20 { 21 pre(u,k); 22 if(sz[u]>sz[son[k]]) son[k]=u; 23 sz[k]+=sz[u]; 24 } 25 r[k]=dfstime; 26 } 27 void del(int k) 28 { 29 for(int i=l[k];i<=r[k];++i) 30 { 31 int u=dfn[i]; 32 f[val[u]]=0; 33 } 34 } 35 void ins(int k) 36 { 37 for(int i=l[k];i<=r[k];++i) 38 { 39 int u=dfn[i]; 40 f[val[u]]=max(f[val[u]],dep[u]); 41 } 42 } 43 void dfs(int k) 44 { 45 for(auto u:g[k]) 46 { 47 if(u==son[k]) continue; 48 dfs(u); 49 ans[k]=max(ans[k],ans[u]); 50 del(u); 51 } 52 if(son[k]) dfs(son[k]),ans[k]=max(ans[k],ans[son[k]]); 53 for(auto u:g[k]) 54 { 55 if(u==son[k]) continue; 56 for(int i=l[u];i<=r[u];++i) 57 { 58 int v=dfn[i]; 59 for(int j=0;j<22;++j) 60 if(f[val[v]^(1<<j)]) 61 ans[k]=max(ans[k],f[val[v]^(1<<j)]+dep[v]-2*dep[k]); 62 if(f[val[v]]) 63 ans[k]=max(ans[k],f[val[v]]+dep[v]-2*dep[k]); 64 } 65 ins(u); 66 } 67 int v=k; 68 for(int j=0;j<22;++j) 69 if(f[val[v]^(1<<j)]) 70 ans[k]=max(ans[k],f[val[v]^(1<<j)]+dep[v]-2*dep[k]); 71 if(f[val[v]]) 72 ans[k]=max(ans[k],f[val[v]]+dep[v]-2*dep[k]); 73 f[val[k]]=max(f[val[k]],dep[k]); 74 } 75 int main() 76 { 77 bin[0]=1; 78 for(int i=1;i<=22;++i) bin[i]=bin[i-1]*2; 79 scanf("%d",&n); 80 for(int i=2;i<=n;++i) 81 { 82 int fa; 83 char s[2]; 84 scanf("%d%s",&fa,s); 85 g[fa].push_back(i); 86 val[i]=bin[s[0]-\'a\']; 87 } 88 pre(1,0); 89 dfs(1); 90 for(int i=1;i<=n;++i) printf("%d ",ans[i]); 91 return 0; 92 }
3、codeforces 570D
题意:
有一个n个点的树,每个点有个点权,是个a~z的字母。有m个询问(vi,hi),问以vi为根的子树中所有深度为hi的点能否重排成一个回文串
分析:
仍旧考虑状态压缩,把字母压成二进制,把询问离线到每个点上
然后同样dsu on tree,每次用全局数组记录res[i]记录下深度为i的所有点点权的异或和,然后就可以判断了
时间复杂度O(26nlogn)
4、codeforces 246E
题意:
一棵树,每一个点有一个颜色(字符串),每一次询问以某一个点为根的子树中与其距离为k的点有多少种颜色。
分析:
同样dsu on tree,每次需要统计某个深度有多少个颜色,那么只需要每个深度挂一个set就行了
时间复杂度O(nlog^2n)
5、codeforces 208E
题意:
给出一棵家谱树,定义向上走k步到达的节点为该点的k-ancestor。每次询问与v同P-ancestor的节点有多少个
分析:
首先我们可以利用倍增把问题转换成以p为根的子树,深度为h的点有多少个
这样就能用dsu on tree轻松解决了
时间复杂度O(nlogn)
6、bzoj2599
题意:
给出N(1 <= N <= 200000)个结点的树,求长度等于K(1 <= K <= 1000000)的路径的最小边数
分析:
本来是一个点分治,然而我们也可以用dsu on tree来做
每条路径在lca处统计
我们可以记录下长度为某个值时候深度的最小值,然后每次合并时候更新答案就行了
时间复杂度O(nlogn)
7、bzoj3681
题意:

分析:
dsu on tree除了可以处理子树统计问题,还可以利用其轻重边剖分的启发式思想去优化复杂度
这种东西一看就是用数据结构去优化网络流建边
考虑从底向上建出每个点的子树的权值线段树,这个显然点数太大不能接受
即使是启发式合并,那如果一条链的情况也会爆炸(每个点被放入了n个线段树中,点数是n^2)
对于一个点u,我们先让他继承他的重儿子的权值线段树,即弄成可持久的
然后把其它轻儿子插入到这个可持久化线段树中
因为每个点最多被插入log次,每次插入一个可持久化线段树会带来log的时间和空间开销
所以最终的点数和边数都是O(nlog^2n)级别的
然后大约是6w个点,24w条边跑最大流,因为图比较稀疏,跑得还是很快的

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=10000,inf=1e9; 4 struct Edge 5 { 6 int from,to,flow; 7 }edge[maxn*250+5]; 8 vector <int> h[maxn+5]; 9 int head[maxn*100+5],nx[maxn*250+5]; 10 int ch[maxn*100+5][2]; 11 int a[maxn+5]; 12 int step[maxn*100];//从源点到点x的距离 13 int iter[maxn*100];//定点x的第几条边开始有用 14 int n,m,S,T,len,sz; 15 void addedge(int from,int to,int cap) 16 { 17 ++len; 18 edge[len]={from,to,cap}; 19 nx[len]=head[from]; 20 head[from]=len; 21 ++len; 22 edge[len]={to,from,0}; 23 nx[len]=head[to]; 24 head[to]=len; 25 } 26 void bfs(int S) 27 { 28 memset(step,-1,sizeof(step)); 29 step[S]=0; 30 queue<int> q; 31 q.push(S); 32 while(!q.empty()) 33 { 34 int v=q.front(); 35 q.pop(); 36 for(int i=head[v];i!=-1;i=nx[i]) 37 { 38 Edge &e=edge[i]; 39 if(e.flow>0&&step[e.to]<0) 40 { 41 step[e.to]=step[v]+1; 42 q.push(e.to); 43 } 44 } 45 } 46 } 47 int dfs(int v,int t,int f) 48 { 49 if(v==t) return f; 50 for(int i=iter[v];i!=-1;i=nx[i]) 51 { 52 iter[v]=i; 53 Edge &e=edge[i]; 54 if(e.flow>0&&step[e.to]>step[v]) 55 { 56 int d=dfs(e.to,t,min(e.flow,f)); 57 if(d>0) 58 { 59 e.flow-=d; 60 edge[i^1].flow+=d; 61 return d; 62 } 63 } 64 } 65 return 0; 66 } 67 int maxflow(int S,int T) 68 { 69 int flow=0; 70 for(;;) 71 { 72 bfs(S); 73 if(step[T]<0) return flow; 74 for(int i=0;i<=sz;++i) iter[i]=head[i]; 75 int f; 76 while((f=dfs(S,T,inf))>0) 77 flow+=f; 78 } 79 } 80 int change(int last,int l,int r,int x,int id) 81 { 82 int k=++sz; 83 ch[k][0]=ch[last][0],ch[k][1]=ch[last][1]; 84 addedge(k,last,inf); 85 if(l==r) 86 { 87 addedge(k,id,inf); 88 return k; 89 } 90 int mid=(l+r)>>1; 91 if(x<=mid) ch[k][0]=change(ch[last][0],l,mid,x,id),addedge(k,ch[k][0],inf);else ch[k][1]=change(ch[last][1],mid+1,r,x,id),addedge(k,ch[k][1],inf); 92 return k; 93 } 94 int siz[maxn+5],son[maxn+5]; 95 int root[maxn+5],l[maxn+5],r[maxn+5],dfn[maxn+5]; 96 int dfstime=0; 97 void pre(int k) 98 { 99 siz[k]=1; 100 l[k]=++dfstime; 101 dfn[dfstime]=k; 102 for(int i=0;i<h[k].size();++i) 103 { 104 int u=h[k][i]; 105 pre(u); 106 if(siz[u]>siz[son[k]]) son[k]=u; 107 siz[k]+=siz[u]; 108 } 109 r[k]=dfstime; 110 } 111 void ins(int k,int &root) 112 { 113 for(int i=l[k];i<=r[k];++i) 114 root=change(root,1,n,a[dfn[i]],dfn[i]); 115 } 116 void dsu(int k) 117 { 118 for(int i=0;i<h[k].size();++i) dsu(h[k][i]); 119 root[k]=change(root[son[k]],1,n,a[k],k); 120 for(int i=0;i<h[k].size();++i) 121 { 122 123 int u=h[k][i]; 124 if(u!=son[k]) 125 ins(u,root[k]); 126 } 127 } 128 void work(int k,int l,int r,int x,int y,int id) 129 { 130 if(l>r||k==0||l>y||r<x) return; 131 if(x<=l&&r<=y) 132 { 133 addedge(id,k,inf); 134 return; 135 } 136 if(l==r) return; 137 int mid=(l+r)>>1; 138 work(ch[k][0],l,mid,x,y,id); 139 work(ch[k][1],mid+1,r,x,y,id); 140 } 141 142 int main() 143 { 144 len=-1; 145 scanf("%d%d",&n,&m); 146 for(int i=2;i<=n;++i) 147 { 148 int fa; 149 scanf("%d",&fa); 150 h[fa].push_back(i); 151 } 152 for(int i=1;i<=n;++i) scanf("%d",&a[i]); 153 memset(head,-1,sizeof(head)); 154 S=
