题目
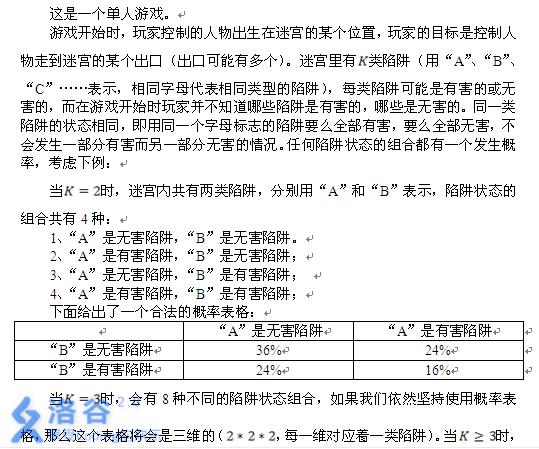



输入格式

输出格式
仅包含一个数字,表示在执行最优策略时,人物活着走出迷宫的概率。四舍五入保留3位小数。
输入样例
4 3 3 2
.$.
A#B
A#C
@@@
143 37 335 85 95 25 223 57
输出样例
0.858
提示

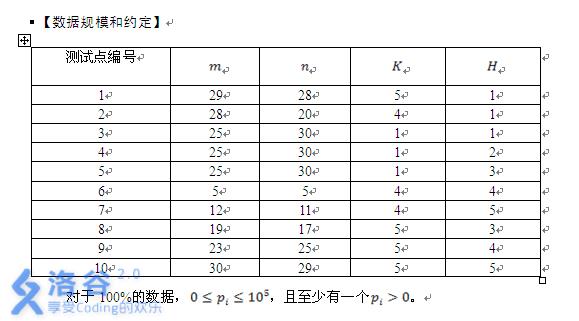
题解
毒瘤dp题
我们设\\(f[x][y][s][h]\\)表示从点\\((x,y)\\)出发,所有陷阱状态为\\(s\\),生命值为\\(h\\),存活的期望概率
我们枚举邻点,选择存活概率最大的作为当前\\(f\\)的值
除了墙,有以下情况:
①如果是空地或者终点,直接转移\\(f[nx][ny][s][h]\\)
②如果是陷阱:
1、如果陷阱已知
无害则同空地的转移
有害则转移的同时\\(h - 1\\)
2、如果陷阱位置
那么就是\\(g[s][t] * f[nx][ny][s\'][h - 1] + (1 - g[s][t]) * f[nx][ny][s\'\'][h]\\)
其中\\(g[s][t]\\)表示在已知状态为s的情况下,陷阱\\(t\\)有害的概率,可以预处理出来
\\(s\'\\)和\\(s\'\'\\)就是加入新状态的s
至于g数组的预处理,对于每种s,枚举未知位置的子集,将各种情况有害的加到对应陷阱去,然后除以总值
为什么换一个搜索顺序才能A???
#include<iostream>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<algorithm>
#define REP(i,n) for (int i = 1; i <= (n); i++)
using namespace std;
inline int read(){
int out = 0,flag = 1; char c = getchar();
while (c < 48 || c > 57){if (c == \'-\') flag = -1; c = getchar();}
while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
return out * flag;
}
double f[32][32][250][6],g[250][6],p[100];
int vis[32][32][250][6],bin[10];
int n,m,K,H,Sx,Sy,X[4] = {1,0,-1,0},Y[4] = {0,-1,0,1};
int G[32][32];
void init(){
n = read(); m = read(); K = read(); H = read();
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++){
char c = getchar();
while (!isprint(c)) c = getchar();
if (c == \'.\') G[i][j] = 0;
else if (c == \'#\') G[i][j] = -1;
else if (c == \'$\') G[i][j] = 0,Sx = i,Sy = j;
else if (c == \'@\') G[i][j] = -2;
else G[i][j] = c - \'A\' + 1;
}
//REP(i,n) {REP(j,m) printf("%d ",G[i][j]); puts("");}
bin[0] = 1;
for (int i = 1; i <= K; i++) bin[i] = bin[i - 1] * 3;
//REP(i,K) printf("%d ",bin[i]); puts("");
int maxv = (1 << K) - 1,maxp = bin[K] - 1;
for (int s = 0; s <= maxv; s++) p[s] = read();
for (int s = 0; s <= maxp; s++){
int e = 0,t = 0; double sum = 0;
for (int i = s,j = 1; j <= K; j++,i /= 3){
if (i % 3 == 0) t |= (1 << j - 1);
else if (i % 3 == 2) e |= (1 << j - 1);
}
for (int i = t; ; i = (i - 1) & t){
int to = (e | i);
sum += p[to];
for (int j = 1; j <= K; j++)
if (to & (1 << j - 1)) g[s][j] += p[to];
if (!i) break;
}
for (int i = 1; i <= K; i++)
g[s][i] /= sum;
}
}
double F(int x,int y,int s,int h){
if (vis[x][y][s][h]) return f[x][y][s][h];
if (h == 0){
vis[x][y][s][h] = 1;
return f[x][y][s][h] = 0;
}
if (G[x][y] == -2){
vis[x][y][s][h] = 1;
return f[x][y][s][h] = 1;
}
vis[x][y][s][h] = 1;
double& ff = f[x][y][s][h];
ff = 0;
int nx,ny;
for (int k = 0; k < 4; k++){
nx = x + X[k];
ny = y + Y[k];
if (nx < 1 || ny < 1 || nx > n || ny > m || G[nx][ny] == -1) continue;
if (G[nx][ny] == 0 || G[nx][ny] == -2){
ff = max(ff,F(nx,ny,s,h));
}
else {
int t = G[nx][ny];
if ((s / bin[t - 1]) % 3 == 1) ff = max(ff,F(nx,ny,s,h));
else if ((s / bin[t - 1]) % 3 == 2) ff = max(ff,F(nx,ny,s,h - 1));
else {
ff = max(ff,g[s][t] * F(nx,ny,s + 2 * bin[t - 1],h - 1) + (1 - g[s][t]) * F(nx,ny,s + bin[t - 1],h));
}
}
}
return ff;
}
int main(){
init();
if (n == 0) return 0;
else printf("%.3lf\\n",F(Sx,Sy,0,H));
return 0;
}