其实有两种方法来解这道题
第一种:找规律(非正经)
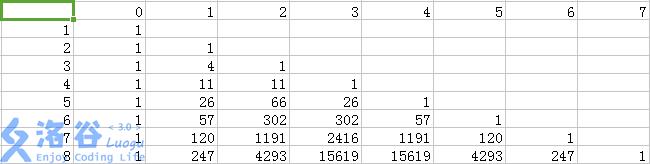
一看,这玩意像是个杨辉三角,还左右对称呢
因为新插入一个数\\(n\\),有\\(n+1\\)个位置可以选,所以总数就乘\\(n+1\\),对应的\\(f[n+1][i]\\)也就等于\\(f[n][i]\\)了大概。可是一看,不大对,好像不是这样。那么就像,反正加一个数要么没变,要么加一个小于号,那么不在\\(f[n+1][i]\\)的一定是分到了\\(f[n+1][i+1]\\)里去了。那么以\\(n=3\\)时为例,\\(f[3][1]*4=4,f[4][1]=1\\)也就是接收了\\(1\\)倍的\\(f[3][1]\\)。那么就有\\(3\\)个分到\\(f[4][2]\\)里去了。\\(f[3][2]*4=16,f[4][2]=11\\),而\\(f[4][2]\\)已经有\\(3\\)个,那么就接收了来自\\(f[4][2]\\)的\\(8\\)个,也就是\\(2\\)倍的\\(f[3][2]\\)。······以此类推,大概就得出了\\(f[n+1][i]+=f[n][i]*(i+1),f[n+1][i+1]+=f[n][i]*(n-i)\\)的规律
-----------------------------------------------手动分割线------------------------------------------------
第二种:数学方法推
这是正经方法
前面说过,加入一个数\\(n\\),有\\(n\\)+\\(1\\)个位置可以选,可以插在两旁或者不等号的位置,因为新插入的数一定是最大的,所以插在最左边多一个大于号,而插在最右边多一个小于号。
那么问题来了,如果插在不等号的位置呢?
首先,明确一下,插入在不等号位置后,一个不等号会变为两个不等号,由于新插入的数一定是最大的,所以这两个不等号中前面的一定是小于号,后面的一定是大于号。那么就很明显了,如果这个位置原来是小于号,那么插入\\(n\\)之后,小于号数不变;如果原来是大于号,那么插入\\(n\\)之后,小于号数+\\(1\\)。那么原本有\\(i\\)个数\\(j\\)个小于号,加上一个数后便会有\\(j+1\\)种小于号不变\\(i-j\\)种小于号\\(+1\\)的情况。
上代码
先是暴力版(通不过的,这是帮助我打出那张图的版本)
#include<iostream>
#include<cstdio>
using namespace std;
const int maxn=1005;
int f[maxn],n,ans[maxn];
bool s[maxn];
void dfs(int step){
if(step>n){
int sum=0;
for(int i=1;i<n;i++)sum+=f[i]<f[i+1]?1:0;
ans[sum]++;
return;
}
for(int i=1;i<=n;i++)
if(!s[i]){
s[i]=1;
f[step]=i;
dfs(step+1);
s[i]=0;
}
}
int main(){
scanf("%d",&n);
dfs(1);
for(int i=0;i<n;i++)printf("%d ",ans[i]);
}
然后上
正常版本
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
const int maxn=1005;
int n,k,f[maxn][maxn];
int main(){
//freopen("num.in","r",stdin);
//freopen("num.out","w",stdout);
scanf("%d%d",&n,&k);
if(k>(n-1)/2)k=n-k-1;
f[1][0]=1;
for(int i=1;i<n;i++){
for(int j=0;j<=(i-1)/2;j++){//由于它类似于杨辉三角,左右对称,所以只求左侧就好
f[i+1][j]=(f[i+1][j]+f[i][j]*(j+1))%2015;
f[i+1][j+1]=(f[i+1][j+1]+f[i][j]*(i-j))%2015;
}
if(i%2==0)f[i+1][i/2]=(f[i+1][i/2]*2)%2015;
}
printf("%d",f[n][k]);
return 0;
}
不喜勿喷