集成学习——Boosting(GBDT,Adaboost,XGBoost)
Posted 杰哥哥是谁
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了集成学习——Boosting(GBDT,Adaboost,XGBoost)相关的知识,希望对你有一定的参考价值。
集成学习中还有一个重要的类别是Boosting,这个是基学习器具有较强依赖串行而成的算法,目前主流的主要有三个算法:GBDT,Adaboost,XGBoost
这个链接可以看看:https://www.cnblogs.com/willnote/p/6801496.html
不同点:
1、adaboost使用的是指数损失(其实也可以使用别的损失函数,不过指数损失比较好解释),直接偏导数等于0(直接让损失函数变最小)来求得样本还有决策树的权重,
而gbdt和xgboost用得都是梯度下降算法,其中gbdt在分类的模型上用得是对数损失,因为分类不可导,只能使用指数或者对数损失,如果使用指数损失,其实就有点变成adaboost了
2、gbdt其实是泰勒一阶展开,而xgboost是二阶展开,所以收敛速度更快
boosting算法的原理如下:
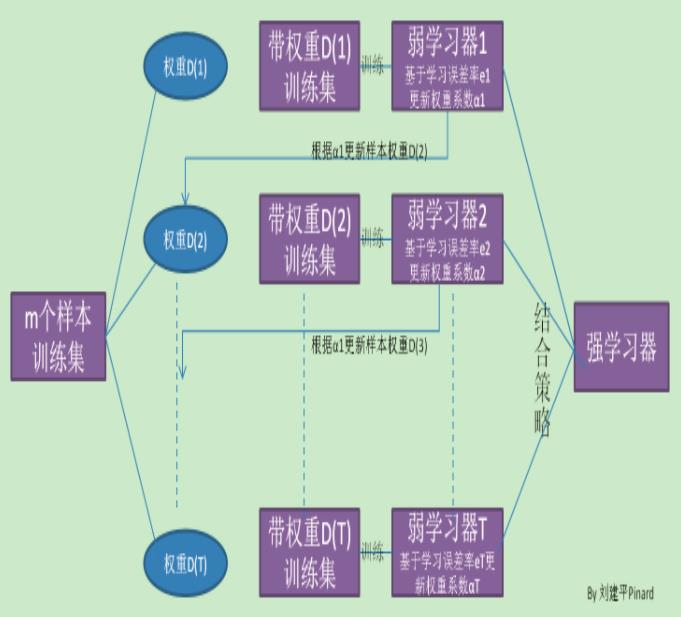
1、GBDT
gbdt和xgboost其实都是回归树!!!因为都用到了导数的性质,所以输出值都不能是0,1 必须要概率形式,不然不可导。概率形式在转成0,1
一、原理

解释:我们机器学习的目的都是为了让损失函数取得最小,这里损失函数可以是很多种,比如平方和损失,绝对值损失,指数对数损失等等,
1、假定我们现在已经知道了我们的损失函数
2、假定我们GBDT产生的最终的F分类器是有许多个f加权得到的的

1、现在我们给定初始的F0模型,这里可以直接给一个常数r让这个损失函数取最小,比如如果损失函数是平方损失,那么r就是均值,如果是绝对值损失函数,那么r就是中位数,
如果是什么别的损失函数,反正是有一个固定常数让他最小
2、给定F0之后我们想要推下一个F1,前面我们假设了是由前m-1个模型在家第m个分类器之后成为最终的F的,所以我们这里需要求得我们选择哪个f能够使得我们Fm-1与他相加后会使得损失函数最小呢
也就是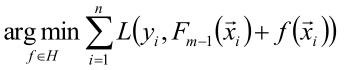 我们要取什么让损失函数最小,那这个f就是我们要的,然后得到这个f再加上前面的Fm-1就是我们最终的模型(其实这里没什么用,就是说一下思想)
我们要取什么让损失函数最小,那这个f就是我们要的,然后得到这个f再加上前面的Fm-1就是我们最终的模型(其实这里没什么用,就是说一下思想)

1、现在问题来了,怎么求这个f呢,我们使用梯度下降算法来求,这里的梯度算法是这样的,纵坐标是损失函数值,横坐标是tree,我们要做的梯度是随着树的增加,损失函数变小
2、所以我们就把当前截止已经形成的Fm-1模型沿着他的损失函数负梯度方面进行计算来得到最终的Fm模型
二、步骤
1)回归算法
1、首先初始化第一个弱学习器: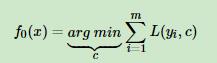 ,这里一定存在一个参数C使得这个损失函数最小,前面说过
,这里一定存在一个参数C使得这个损失函数最小,前面说过
2、从第t轮开始,t=1,2,3,4.。。t:
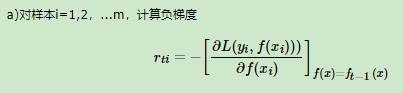 ,这里我们需要计算每个样本应该如何沿着负梯度方向变化才能够使得这个模型提升
,这里我们需要计算每个样本应该如何沿着负梯度方向变化才能够使得这个模型提升

这个意思其实就是:我们拿到每个样本应该变化多少了,现在我们建立一个树来预测这个应该变化多少,预测值加入到前面t-1轮形成的模型中,得到t轮的最终模型
3、这个时候再把t轮的模型拿来预测,预测值假设是f(t),再计算这个预测值与实际值的偏差(还是按照损失函数负梯度公式来做),差值再做模型建立,再加上原来t轮形成的模型中,得到ft+1轮
这里解释一下:我们想要沿着损失函数负梯度方向发展,所以你就要知道想得到这样的损失函数,你每个样本应该怎么样变化,也就是每个样本还差多少才能够让损失是沿着负梯度方向发展的,所以我们才要把每个样本的误差值拿来做预测,如果刚好预测全对,也就是需要偏差的量我们预测全对,那么原来的f0加上我们这一轮预测的误差量就会使得样本预测全部正确。理解这段话非常关键!!!
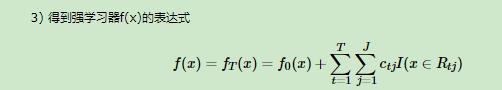
2)分类算法

三、正则化
1、一种是跟adaboost一样,对于弱学习器增加一个步长v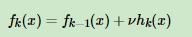
2、
第二种正则化的方式是通过子采样比例(subsample)。取值为(0,1]。注意这里的子采样和随机森林不一样,随机森林使用的是放回抽样,而这里是不放回抽样。如果取值为1,则全部样本都使用,等于没有使用子采样。如果取值小于1,则只有一部分样本会去做GBDT的决策树拟合。选择小于1的比例可以减少方差,即防止过拟合,但是会增加样本拟合的偏差,因此取值不能太低。推荐在[0.5, 0.8]之间。
使用了子采样的GBDT有时也称作随机梯度提升树(Stochastic Gradient Boosting Tree, SGBT)。由于使用了子采样,程序可以通过采样分发到不同的任务去做boosting的迭代过程,最后形成新树,从而减少弱学习器难以并行学习的弱点。
3、对于弱学习器即CART回归树进行正则化剪枝。
2、XGBoost
XGBoost是GBDT的一个升级,gbdt使用泰勒一阶展开,而xgboost使用二阶
 其中
其中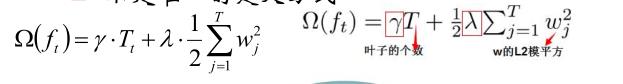
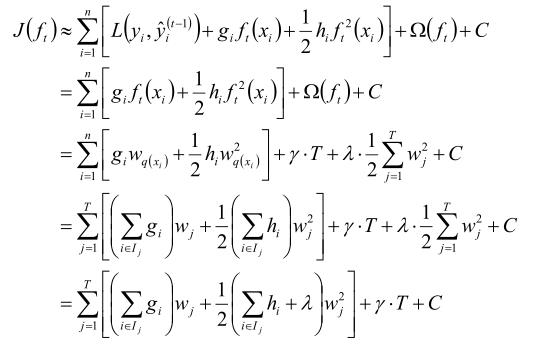

3、Adaboost
Adaboost的基本思想是这样的:
1、一开始所有的样本权重全部相等,训练处第一个基分类器,根据这个基分类器对样本进行划分
2、从第二轮开始针对前一轮的分类结果重新赋予样本权重,对于分类错误的样本权重加大,正确的样本权重减少。
3、之后根据新得到样本的权重指导本轮中的基分类器训练,即在考虑样本不同权重的情况下得到本轮错误率最低的基分类器。重复以上步骤直至训练到约定的轮数结束,每一轮训练得到一个基分类器。
可以想象到,远离边界(超平面)的样本点总是分类正确,而分类边界附近的样本点总是有大概率被弱分类器(基分类器)分错,所以权值会变高,即边界附近的样本点会在分类时得到更多的重视。
步骤说明:
1)分类问题
1、对于所有的样本,我们先赋予初始权重,分别都相等1/M
2、选择一个基分类器对样本进行分类,计算经过这个基分类器分类后的误差率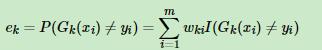 ,其中w为样本权重,
,其中w为样本权重,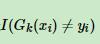 这个函数表示若预测值与实际值不一致返回1,否则返回0
这个函数表示若预测值与实际值不一致返回1,否则返回0
经过以上的计算,就会计算出所有分类错的样本的误差率
3、计算这个基学习器的权重系数: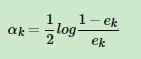 ,这个公式说明:如果误差率ek越小,那么
,这个公式说明:如果误差率ek越小,那么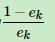 越大,那么log之后也越大,因此这个系数ak也越大,这说明如果误差率越小,学习期的系数权重越大(注意跟下面的样本系数不一样啊!!!)
越大,那么log之后也越大,因此这个系数ak也越大,这说明如果误差率越小,学习期的系数权重越大(注意跟下面的样本系数不一样啊!!!)
4、更新样本的权重,把错分的权重加大,正确的权重减小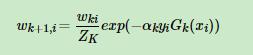 其中ZK是规范化因子
其中ZK是规范化因子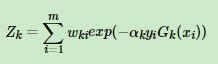
这里先解释第一个公式,也就是权重公式:ex函数图像可以去百度一下,是一个过0,1点的递增函数,也就是如果分类错误,那么yi*Gk(xi)就不是同号就<0,那么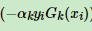 这个就会比较大,大于1,也就是原来的权重基础上乘以一个比1大的数字,调大了这个权重,同理,如果分类正确就会调小,也就是,如果分错了,误差率变大了,样本权重变大(记住跟系数权重不一样啊!!!)
这个就会比较大,大于1,也就是原来的权重基础上乘以一个比1大的数字,调大了这个权重,同理,如果分类正确就会调小,也就是,如果分错了,误差率变大了,样本权重变大(记住跟系数权重不一样啊!!!)
第二个公式是规范化因子,因为如果不除以这个因子,会导致权重总和不等于1,除掉这个因子之后所有权重加起来又等于1了
5、根据不同权重的样本在做第二个基分类器,同样计算权重,一直轮
6、最后通过训练出来的K个分类器进行决策: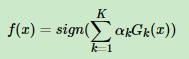
2)回归问题
回归问题不同的是误差率的计算:
1、对于所有的样本,我们先赋予初始权重,分别都相等1/M
2、选择一个基学习期进行学习,得到第一个模型
首先计算最大误差: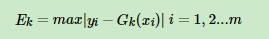 ,接着计算每个样本的相对误差
,接着计算每个样本的相对误差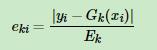 ,每个样本的相对误差加权求和得到这个基学习器的误差率ek
,每个样本的相对误差加权求和得到这个基学习器的误差率ek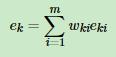
注意:
同样根据误差率更新基学习器权重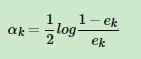 ,再更新样本权重:
,再更新样本权重: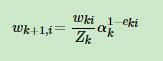 其中Z也是规范化因子
其中Z也是规范化因子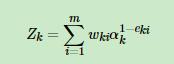
这里的公式这么理解:如果这个样本的误差率比较大,那么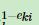 就会比较小,由于ak是一个小于1的数,所以
就会比较小,由于ak是一个小于1的数,所以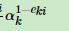 这个就会比较大,同时样本权重就加大了,
这个就会比较大,同时样本权重就加大了,
3、最后也是通过训练出来的K个分类器进行决策: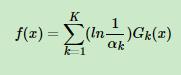
损失函数优化:
前面我们只是介绍了计算权重、系数的公式,没有解释原因,以下推导这个公式产生的原因
Adaboost是模型为加法模型,学习算法为前向分步学习算法,损失函数为指数函数的分类问题。
加法模型很好理解:因为我们最终决策是根据这K个决策树相加来做决策的
前向分步学习也很好理解:因为t+1轮学习期是根据t轮学习期的结果进行的
损失函数为指数函数:真是难理解这里
定义损失函数为:
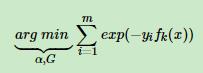 这里这样理解:如果yi与预测值f(x)一致,那么想成是>0,那么指数就会比较小,比1小;如果yi与预测值f(x)不一致,那么想成是<0,加个负号大于0,指数就变大大于1,把所有的样本的这个指数值累加,如果能够取最小,说明都分类对了嘛,所以这个是他的损失函数,完美!!!
这里这样理解:如果yi与预测值f(x)一致,那么想成是>0,那么指数就会比较小,比1小;如果yi与预测值f(x)不一致,那么想成是<0,加个负号大于0,指数就变大大于1,把所有的样本的这个指数值累加,如果能够取最小,说明都分类对了嘛,所以这个是他的损失函数,完美!!!
由于我们前面了解到了,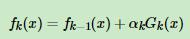 ,所以代入得到
,所以代入得到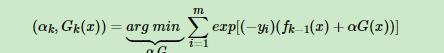
 所以损失函数再变化成下面的样子
所以损失函数再变化成下面的样子
然后下面重点来了:
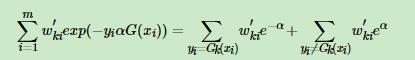 这个可以分成yi=G(x)和yi不等于G(x)两部分相加,以为等于是1,不等于是-1,所以化简成那样
这个可以分成yi=G(x)和yi不等于G(x)两部分相加,以为等于是1,不等于是-1,所以化简成那样
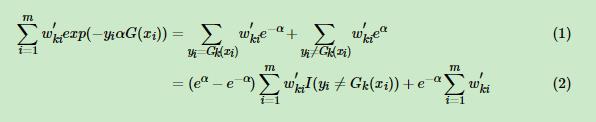 这里从1到2,先把
这里从1到2,先把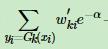 这个看作是总的减去yi不等于G(I)的,然后再跟后面的合并
这个看作是总的减去yi不等于G(I)的,然后再跟后面的合并
不等于那一部分提取出来,加上后面的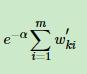 这个是总的,接下来就可以求导了,我们对a求导得到
这个是总的,接下来就可以求导了,我们对a求导得到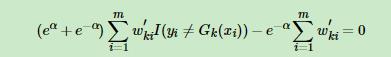
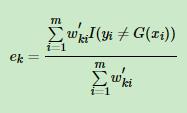 然后代入
然后代入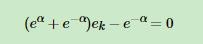 最后得到a的计算公式
最后得到a的计算公式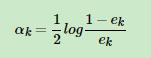 ,这个就解释了前面为什么用这个公式,
,这个就解释了前面为什么用这个公式,
最后想说真是太他么难了!!
Adaboost算法正则化:
对于Adaboost算法我们也可以加入正则化,其实就是加在每个基分类器前面

以上是关于集成学习——Boosting(GBDT,Adaboost,XGBoost)的主要内容,如果未能解决你的问题,请参考以下文章