title: 斯坦福-随机图模型-week3.0
tags: note
notebook: 6- 英文课程-9-Probabilistic Graphical Models 1: Representation
斯坦福-随机图模型-week3.0
马尔科夫网络
pairwise markov networks 成对马尔科夫模型
图论模型中有有向图和无向图，对于无向图来说，运用到随机图论中就是马尔科夫模型。
在马尔科夫模型中，有一种模型十分有趣，他是成对马尔科夫模型。
我们首先看一个例子：
四个学生同时进行学习，并且他们会相互进行影响。
infinity function / compatibility funcutions.
加入老师再课堂上出现了一次口误，那个他们中的误解是如何进行相互影响的呢？
这个表格描述了两个人的快乐程度，如果两个人都听对了，那么他们都会获得30的快乐程度，如果两个人都听错了，那么他们的快乐程度也会很高。如果一个人听对了另外一个人听错了，那么他们的快乐程度就会相对比较低。
同样的我们可以为所有的联系都定义他们的快乐程度：
我们可以将所有的快乐程度相乘起来来获得一个综合的指数：
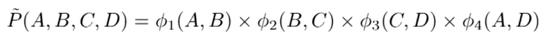
然后我们就可以对所有的幸福程度进行汇总，然后乘以相应的归一化系数，将他的和归为1。
好的我们现在可以讨论下理论上的事情了：
相关的术语
边界概率
条件概率- 边界概率的条件概率
正常吉布斯分布
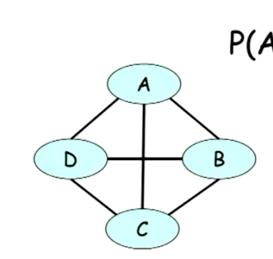
假设再一个全部互联的马尔科夫模型中。
我们考虑一个问题
**再一个全互联的马尔科夫网络中，如果共有n个变量，每个变量有d个值，那么一共需要多少参数才能描述我们的马尔科夫网络呢。
这个问题我们这样分析他，我们有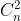
个边，因此关联的矩阵的边长是d
所以我们有。
吉布斯分布式用来简便的生成这些参数的。
我们使用标准参数
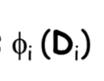
就是再重复我们前面例子里的工作，我们通过定义每条边的情况定义所有的gibbs因子：
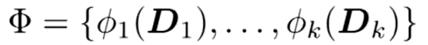
然后把他们乘在一起：
然后我们对得到的数据进行标准化
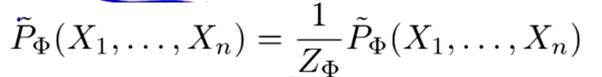
触发形马尔科夫网络
触发形马尔科夫网络是一种，形成环的网络，比如是这样：
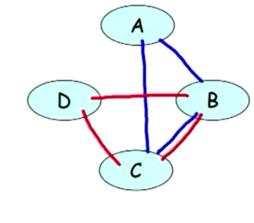
在上图中分别描述了
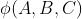和
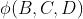形成的环
因子化
直接使用问题讨论：
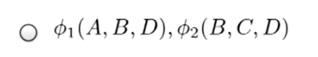
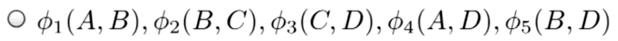
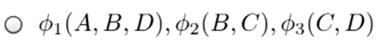
上面这三个都是正确的，因为他们都能表示相应的拓扑结构。
条件随机领域
