一、学前准备

二、掌握外延关系,快速解决数量题
1、4种外延关系


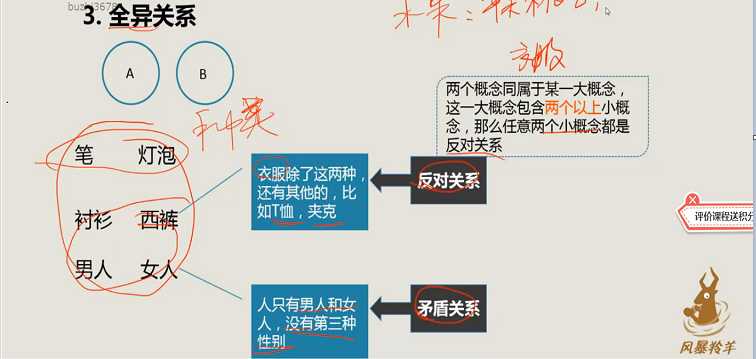
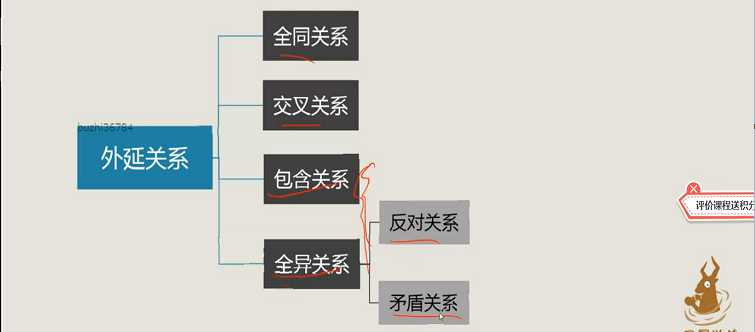
2、例题
注:很明显的外延关系数量题,根据描述画出外延关系图:图之间是全异关系时人数最多,是包含关系时人数最少。



三、逻辑题中的“有些”
1、“有些”的含义

【简单记】“有些”其实就是包含“一个”、“一部分”和“全部”这三种情况。注:很容易把“所有”这种情况忽略。
2、“有些”的4个规则

3、例题


四、直言命题的矛盾关系
1、矛盾关系


2、直言命题

【简单记】所有→全称命题;有些→特称命题;xxx→单称命题。
3、具有矛盾关系的直言命题
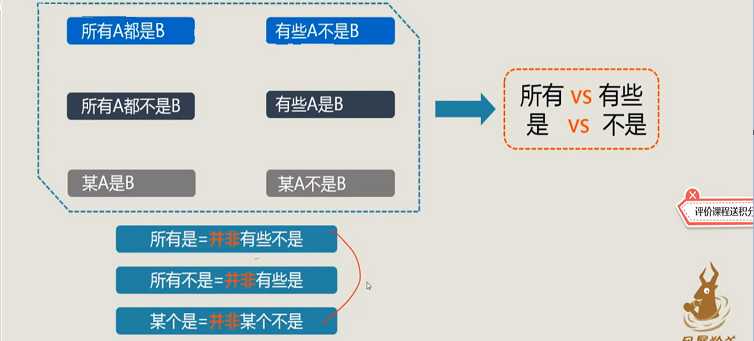
【简单记】特征词汇:“所有”和“有些”对应;“是”和“不是”对应。将一个直言命题中的两个特征词汇换为对应的特征词汇,得到的直言命题就是它的矛盾命题。
4、例题

【解析】将描述用更明显的直言命题来表示,“不都”即“不是所有”:“不是所有品学兼优的学生都读研究生(真)”。它的矛盾命题为描述3,所以3为假。根据“有些”的4个规则,描述4无法确定;3的矛盾命题为““有些品学兼优的学生不读研究生”即描述2,所以2为真,1不确定,选B。

【解析】此类题找到矛盾命题是关键,很明显1和3牌子就是矛盾关系,只有一个牌子为真,那么2和4一定为假,进一步又可推导出4为假,选D。

五、直言命题的反对关系和推出关系
1、上反对关系和下反对关系



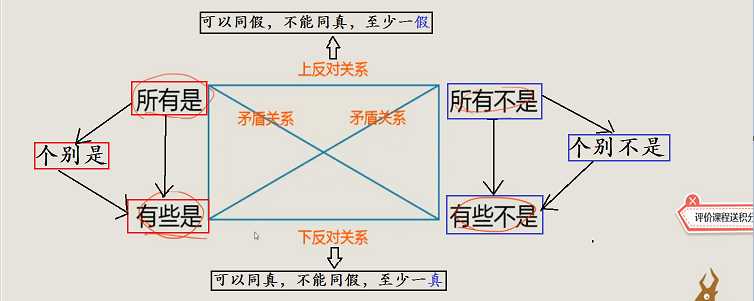
【注】其实记住直言命题关系图就可以解释上面所说的:“有些”4个规则和直言命题矛盾关系。所以需要牢记。
2、例题

【解析】甲乙为上反对关系,“可以同假,不能同真,至少一假”。而题目只有一个错误,所以丙为真,选B。

【解析】1和2为下反对关系,“可以同真不能同假,至少一真”,题目中只有一个真,所以3为假,则1真2假,2的矛盾语句为“所有的人都会用WIn8”,选A。

六、三段论规则
1、三段论形式
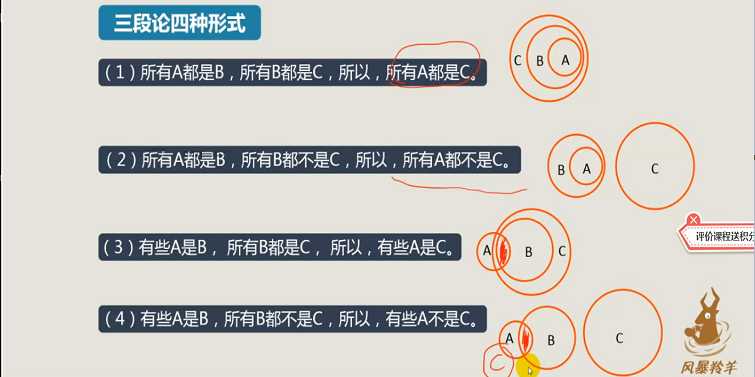
2、规则

【注】三段论就是由A和B,B和C两个关系推导出A和C的关系。其中B称为中项。
(1)全肯必肯:在三段论推导中,两个肯定语句必导出肯定句;
(2)一特必特,不可全特:特指特称命题(“有些”)。这句话是指有特称命题作为推导条件时推导出来的结论一定时特称命题,且不能以两个特称命题作为推论条件。
(3)一否全否,不可全否:和(2)类似,这里的否是指否定句。
(4)中项规则:中项指B,作为推论条件时至少被被全称(所有B...)或被否定(B不是...)一次。
3、例题

【解析】符合三段论题型,但是有4个主体:A“深受儿童喜爱的玩具”、B“中国制造”、C“玩具是安全又环保的”、D“受广大家长欢迎的”,这四个主体都可以从中选三个作为三段论的主体。这种组合有4种,所以一般情况我们考虑按照答案逐一排查即可。但本题有一个特点,就是这些推论条件语句都是肯定句。根据“全肯必肯”可判断推论一定是肯定句,只有A不是,选A。

【解析】很明显的三段论题型。第一句是特称肯定句,第二句是否定句,根据“一特必特,不可全特”和“一否必否,不可全否”可判断推论是“特征否定句”,只有D符合。

【解析】三段论题。第一句是特称肯定句,第二句需要补充,结论是特征肯定句,根据“一特必特,不可全特”推论出条件语句不能是特称语句,排除BCD,选A。

【解析】三段论题型。第一句是特称命题,第二句需要补充。结论是特称肯定句,和例3一样,所以第二句不能是特称语句,排除 CD。到这里可以根据选项来一一排除也可以根据另一个规则“中项规则”,中项是没有出现在推论里的主体,即“高校教师”,至少被全称或被否定一次,选D。

七、模态命题
1、模态关系反对关系图
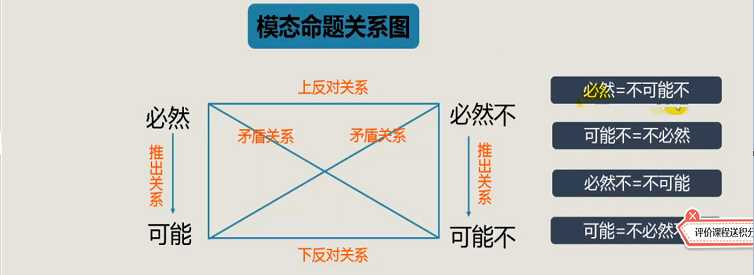
【注】和上面的“直言命题反对关系图”结合着看,一样的规律。

2、例题





八、条件命题
1、条件命题及翻译
- 三种情况:充分、必要、充要(一般不考):

- 充分条件翻译:

- 必要条件

- 推论规则

【注】以上的条件语句都能翻译为A→B的形式,则有以下规律
(1)肯前肯后:A→B,A肯定则B也肯定。
(2)否后否前:A→B,则-B→-A,即否B能推导出否A。
(3)否前,后面不确定:-A无法得出其他推论。
(4)肯后,前面不确定:B无法确定前面是A还是-A。
2、例题

【解析】上面三个推论翻译为三个充分条件推论,根据推论规则,事实是“举办拔河比赛”,对于第一个句子是“肯后不确定”;对于第二个句子是“否后否前”,说明风不大;对于第三个句子是“否前不确定”,所以只有2为真,选B。

【解析】根据条件语句描述翻译为蓝色部分的语句。然后根据推论的4个规律逐一筛选答案即可C。

3、条件命题的矛盾命题

【注】即A→B的矛盾命题为A→-B。


4、条件命题的严谨性

【注】根据“否前,后面不确定”和“肯后,前面不确定”这两种不确定情况,逻辑上为遵循严谨性,整个充分条件视为真。【将不确定命题视为真】

【解析】丙不是条件语句,先假设丙为真。对于甲,“否前,后面不确定”,即“条件为假,视整个命题为真”。题意说三个人只有一个人正确,假设不成立。则丙错,即“搞读书演讲、知识竞赛”,则乙真甲假,选A。

【解析】和例3一样。先假设3为真,则2也为真,与题意矛盾。则“甲未被录取”,则1真2假,选B。

九、使用→法解决三段论题型
上面我们遇到的三段论,只需要使用“三段论的4个规则”:

进行解答即可,但有时候题目中包含的“三段论”有些复杂时就不适合使用这些规则来解答,这时我们使用→法来解题会快得多。







十、联言命题(交集)
1、理解联言命题

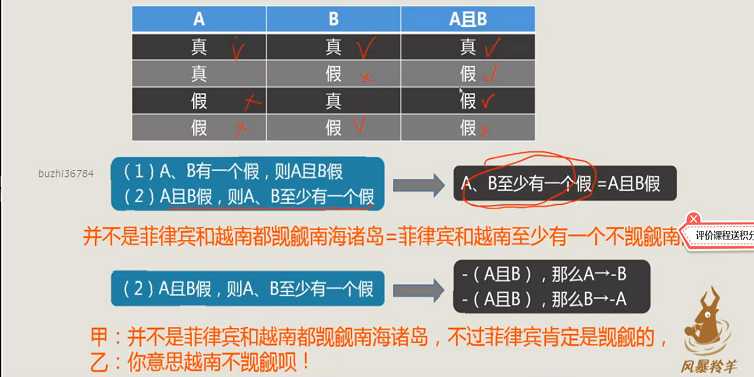
【注】我们可以将联言命题看做两个直言命题的交集来理解:

2、例题

【解析】联言命题,翻译为“钢琴∩吉他”。让联言命题为假,则A或B至少一假即可,则弹钢琴或弹吉他至少不会一项即可。①②③都符合,④是假设不是事实无法反驳。选B

【解析】联言命题,翻译为“英语∩法语”的矛盾命题,即至少不会其中一门语言,有三种可能,选D。

【解析】(1)翻译为“甲∩乙→-丙”;(2)“丙→丁陈述正确”;(3)“只有...才”是充要条件命题,翻译为“丁陈述正确→乙”。(2)(3)推导出乙是杀人犯,而丙有罪根据(1)则甲为假不是杀人犯,选C。
十一、相容选言命题(并集)
1、理解相容选言命题

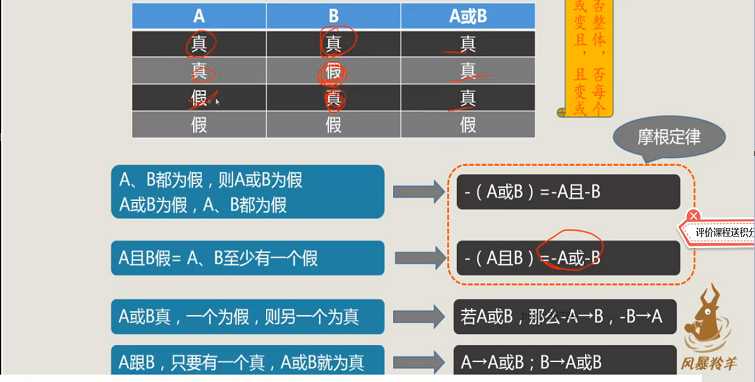
【注】我们可以将相容选言命题看做两个直言命题的并集来理解:

2、例题

【解析】相容选言命题,“质量不好∪价格太高∪广告不好→产品滞销”,现在质量很好,则价格太高和广告不好的原因至少有一个,选C。



十二、不相容选言命题(异或)
1、理解不相容选言命题


【注】我们可以将不相容选言命题看做两个直言命题的并集来理解:

2、例题

【解析】不相容选言命题,“很强的专业⊕长期拼搏→成功的企业家”,已知董事长长期拼搏,第一种情况:没有专业知识,一真一假则结论真,能成为成功的企业家;第二种情况:有专业知识,两个都为真,结论假,不能成为成功的企业家。所以是否成功不确定,选D。



十二、复合命题
1、理解复合命题
复合命题与直言命题相对。简单来说复合命题就是以下几种命题综合考察的题型。
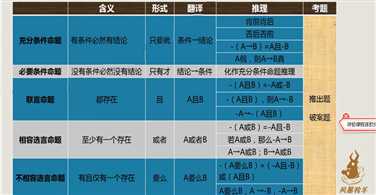
2、例题




十三、朴素逻辑
1、排序题
【注】排序题一般都有大小关系式,一一例举出来就可以就能推导出答案。






2、匹配题
【注】匹配题一般用画表格和排除法来选择答案。







3、破案题
【注】破案题一般使用找突破口、代入答案法、假设法来解答。




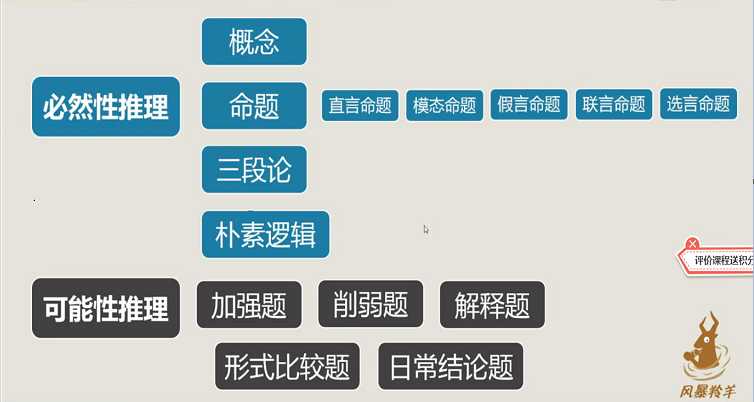
十四、可能性推理体系

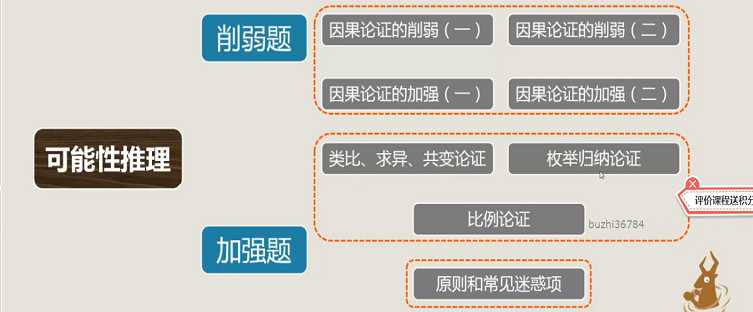
十五、因果论证削弱
1、5个削弱方法

2、例题









十六、因果论证的加强
1、5种加强方法

2、例题








十七、类比论证&求异论证&公变论证的削弱和加强
1、类比论证

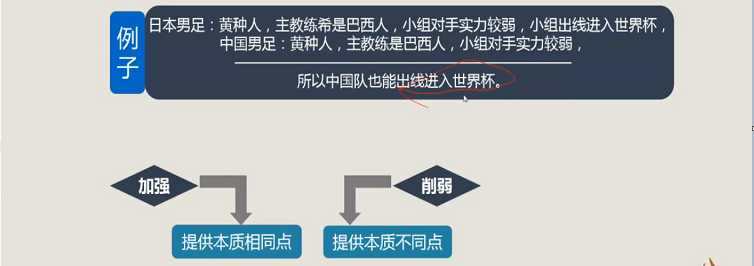

2、求异论证

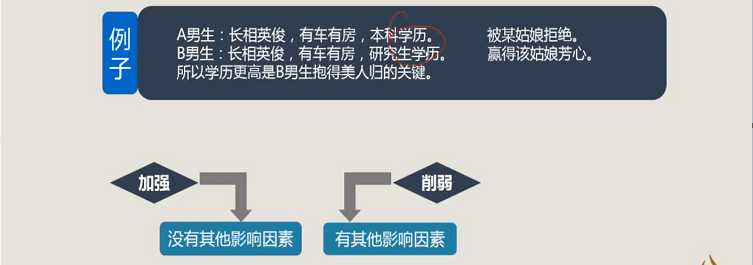

3、共变论证
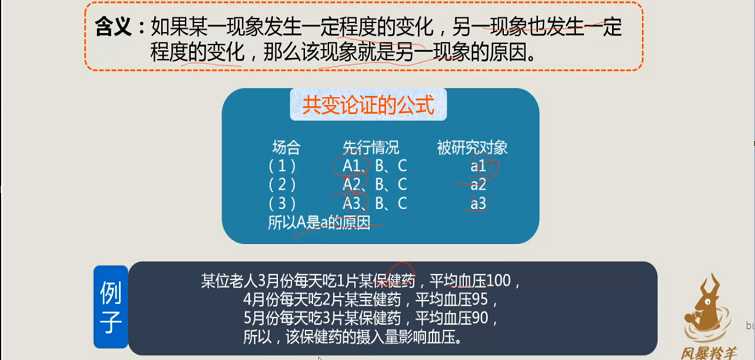
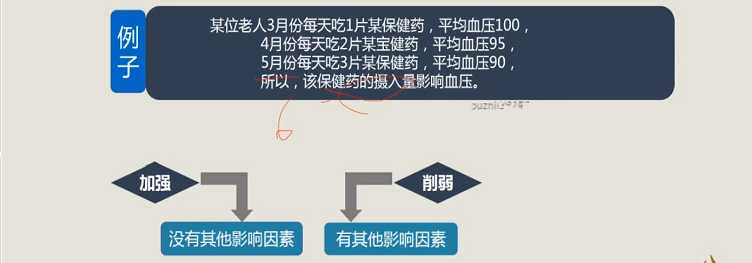

4、小结

十八、枚举论证的削弱和加强
1、理解枚举论证
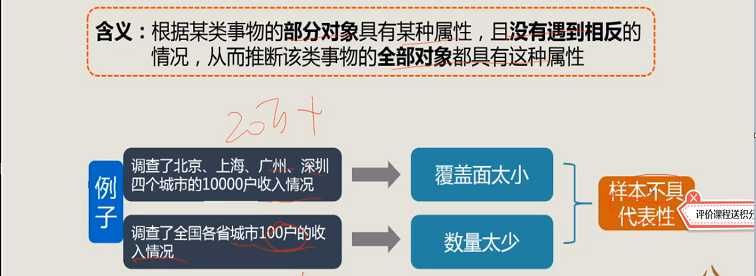
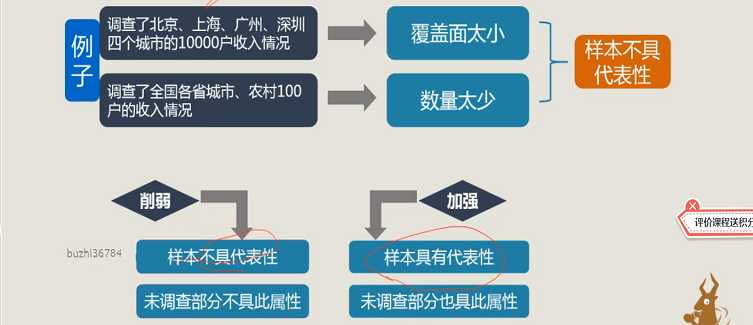
2、例题



3、小结

十九、比例认证的削弱和加强
1、理解比例认证

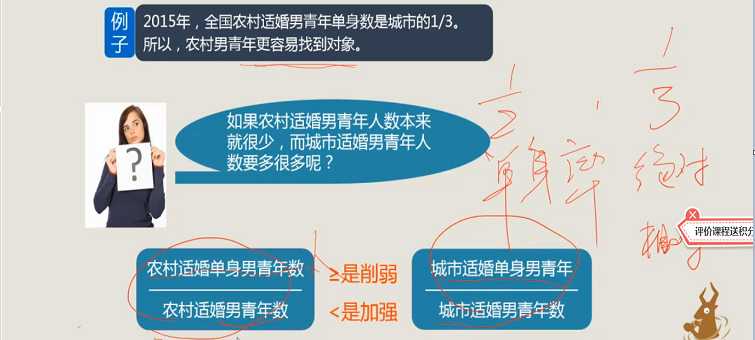

2、例子



二十、削弱题和加强题易混淆的点
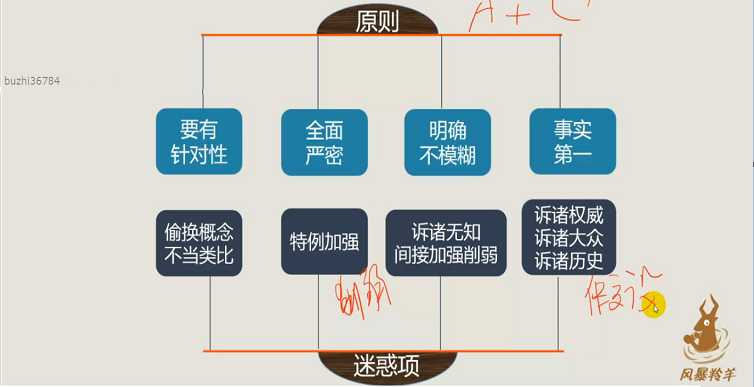





二十一、解释题
1、解释现象



2、解释矛盾




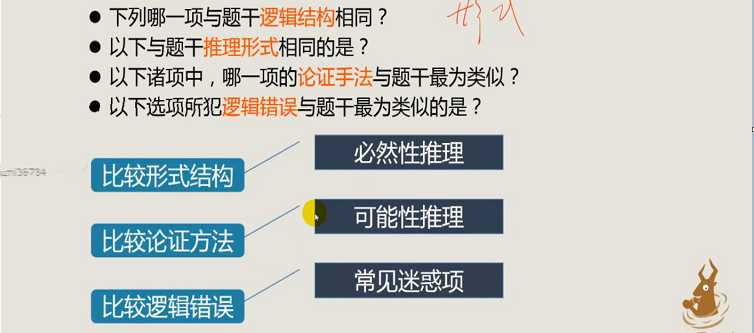
二十二、形式比较题





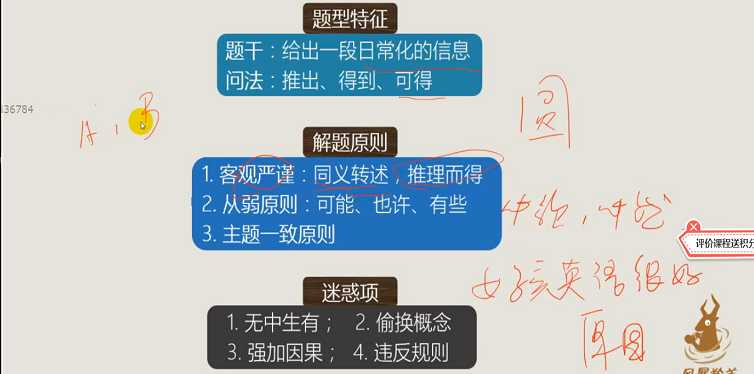
二十三、日常结论题