层次分析法实际应用

Posted 2020-10-27 A piece of summer，a piece of y

应用层次分析法计算水环境管理中社会效益、经济效益和环境效益的权重。

B影响因素（3）：社会效益、经济效益、环境效益。

C方案（4）：均衡考虑三个目标权重；优先考虑社会效益；优先考虑经济效益；优先考虑水环境。

 

 

问卷调查

问卷调查对象为水资源管理方面的工作人员及专家，问卷调查内容要求受调查者根据经验对已识别出的各影响因素的重要性作出评价。在问卷调查中要求受调查者按照标度法对影响因素进行两两比较。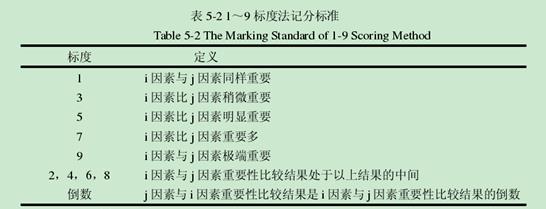

 

 

 

1.     

   判断矩阵 
   

   

    

   
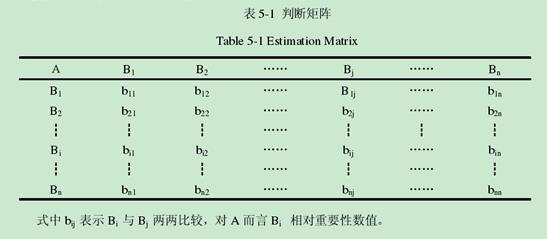
   根据问卷调查结果，得到判断矩阵。（社会效益B₁、经济效益B₂、环境效益B₃）
   A-B判断矩阵

A	B1	B2	B3
B1	1	5	4
B2	1/5	1	2
B3	1/4	1/2	1

B₁-C判断矩阵

B1	C1	C2	C3	C4
C1	1	1/6	4	4
C2	6	1	6	6
C3	1/4	1/6	1	1
C4	1/4	1/6	1	1

B₂-C判断矩阵

B2	C1	C2	C3	C4
C1	1	4	1/6	4
C2	1/4	1	1/6	1
C3	6	6	1	6
C4	1/4	1	1/6	1

    B₃-C判断矩阵

B3	C1	C2	C3	C4
C1	1	4	4	1/6
C2	1/4	1	1	1/6
C3	1/4	1	1	1/6
C4	6	6	6	1

3.    层次单排序 
根据判断矩阵推算各因素的权重，记为W_Bi 。

 

计算

A	B1	B2	B3	MBi		WBi	层  次 单排序
B1	1	5	4	20	2.7144	0.6870	1
B2	1/5	1	2	2/5	0.7368	0.1865	2
B3	1/4	1/2	1	1/8	0.5	0.1265	3
∑					3.9512	1.0000

如果在Matlab中使用eig函数计算，过程及结果如下：

 

 

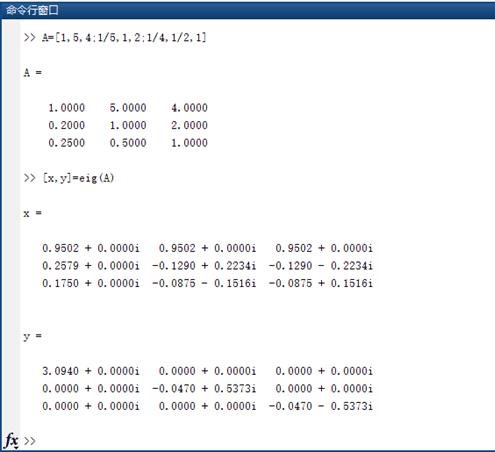
x为矩阵特征向量；y为特征值。（特征值是对角矩阵y 矩阵x的每一列对应一个y中相应列的特征值）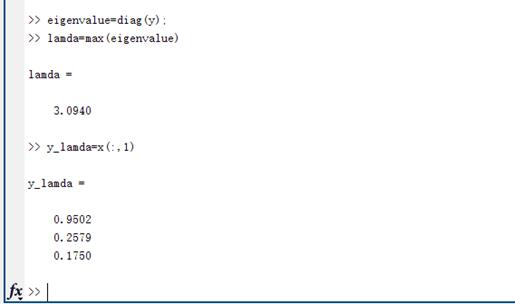

 

 

lamda和y_lamda分别为最大特征值和最大特征值对应的特征向量。
如上数据，矩阵为3X3，一眼就可以看出最大特征值，其他数据量大的时候，便需要这种方法直接得出最大特征值。
我们将得到的特征向量y_lamda [0.9502;0.2579;0.1750]归一化得到[0.6870;0.1865;0.1265]，与上面矩阵方根法得到的结果相同。

B-C权重计算结果

B（1,2,3）
C1	0.2125	0.2125	0.2125
C2	0.6373	0.0751	0.0751
C3	0.0751	0.6373	0.0751
C4	0.0751	0.0751	0.6373
∑	1	1	1

 

4.     层次总排序

	B1（社会效益）	B2（经济效益）	B3（环境效益）	∑
C1（方案1）	0.1445	0.03825	0.0255	0.20825
C2（方案2）	0.433364	0.013518	0.09012	0.455894
C3（方案3）	0.051068	0.114714	0.09012	0.174794
C4（方案4）	0.051068	0.013518	0.076476	0.141062

按方案归一化后：

W（权重）	B1（社会效益）	B2（经济效益）	B3（环境效益）
C1（方案1）	0.6939	0.1837	0.1224
C2（方案2）	0.8070	0.0252	0.1678
C3（方案3）	0.1995	0.4481	0.3524
C4（方案4）	0.3620	0.0958	0.5422

5.     一致性检验