题目
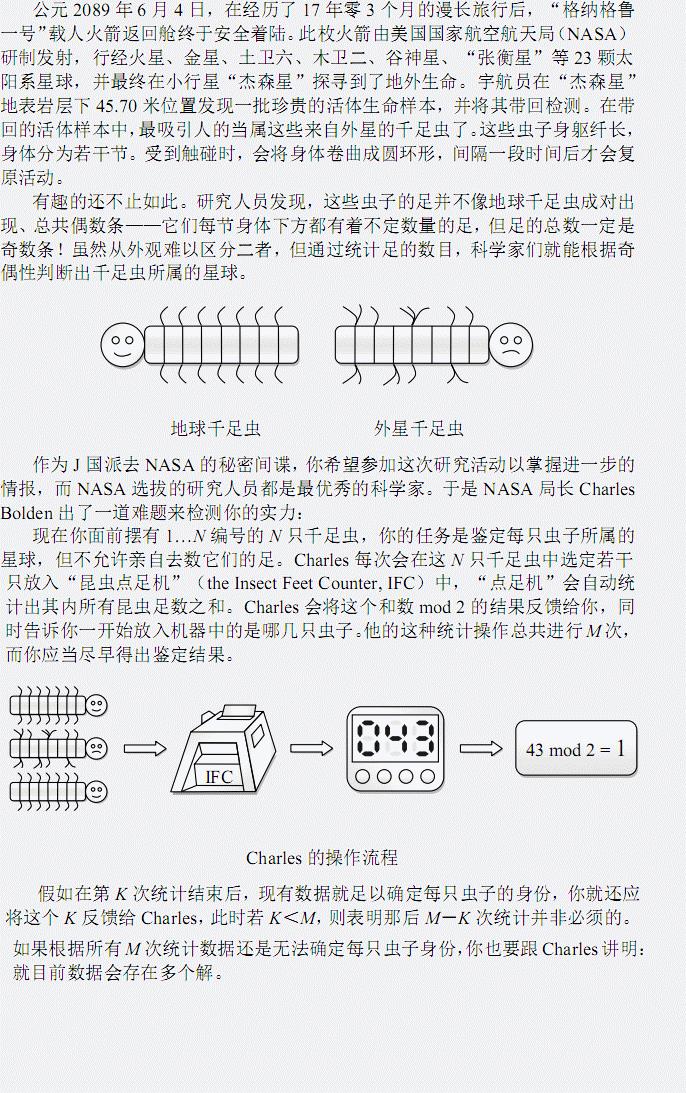
输入格式
第一行是两个正整数 N, M。 接下来 M行,按顺序给出 Charles 这M次使用“点足机”的统计结果。每行 包含一个“01”串和一个数字,用一个空格隔开。“01”串按位依次表示每只虫 子是否被放入机器:如果第 i 个字符是“0”则代表编号为 i 的虫子未被放入,“1” 则代表已被放入。后面跟的数字是统计的昆虫足数 mod 2 的结果。 由于 NASA的实验机器精确无误,保证前后数据不会自相矛盾。即给定数据 一定有解。
输出格式
在给定数据存在唯一解时有 N+1行,第一行输出一个不 超过M的正整数K,表明在第K 次统计结束后就可以确定唯一解;接下来 N 行 依次回答每只千足虫的身份,若是奇数条足则输出“?y7M#”(火星文),偶数 条足输出“Earth”。如果输入数据存在多解,输出“Cannot Determine”。 所有输出均不含引号,输出时请注意大小写。
输入样例
3 5
011 1
110 1
101 0
111 1
010 1
输出样例
4
Earth
?y7M#
Earth
提示
对于 20%的数据,满足 N=M≤20;
对于 40%的数据,满足 N=M≤500;
对于 70%的数据,满足 N≤500,M≤1,000;
对于 100%的数据,满足 N≤1,000,M≤2,000。
题解
奇偶运算【mod 2】可以转化为异或运算
我们就有了m个异或方程组
进行一次高斯消元
无解或多解时,找不到一个j使得系数i为1
唯一解时,最大的被用到的j就是最早出解的位置
#include<iostream>
#include<cstdio>
#include<cmath>
#include<bitset>
#include<cstring>
#include<algorithm>
#define LL long long int
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define BUG(s,n) for (int i = 1; i <= (n); i++) cout<<s[i]<<\' \'; puts("");
using namespace std;
const int maxn = 1005,maxm = 2005,INF = 1000000000;
inline int read(){
int out = 0,flag = 1; char c = getchar();
while (c < 48 || c > 57){if (c == \'-\') flag = -1; c = getchar();}
while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
return out * flag;
}
bitset<1005> a[maxm];
int n,m,ans = 0;
bool gause(){
for (int i = 1; i <= n; i++){
int j = i;
while (!a[j][i] && j <= m) j++;
if (j == m + 1) return false;
ans = max(ans,j);
swap(a[i],a[j]);
for (int k = 1; k <= m; k++)
if (k != i && a[k][i]) a[k] ^= a[i];
}
return true;
}
int main(){
n = read(); m = read(); char c;
for (int i = 1; i <= m; i++){
c = getchar();
while (c != \'0\' && c != \'1\') c = getchar();
for (int j = 1; j <= n; j++) a[i][j] = c - \'0\',c = getchar();
a[i][n + 1] = read();
}
if (!gause()) puts("Cannot Determine");
else {
printf("%d\\n",ans);
for (int i = 1; i <= n; i++)
a[i][n + 1] ? puts("?y7M#") : puts("Earth");
}
return 0;
}