逻辑回归--数据独热编码+数据结果可视化
Posted soyosuyang
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了逻辑回归--数据独热编码+数据结果可视化相关的知识,希望对你有一定的参考价值。
#-*- coding: utf-8 -*- \'\'\' 在数据处理和特征工程中,经常会遇到类型数据,如性别分为[男,女](暂不考虑其他。。。。),手机运营商分为[移动,联通,电信]等,我们通常将其转为数值带入模型,如[0,1], [-1,0,1]等,但模型往往默认为连续型数值进行处理. 独热编码便是解决这个问题,其方法是使用N位状态寄存器来对N个状态进行编码,每个状态都由他独立的寄存器位,并且在任意时候,其中只有一位有效。 可以理解为对有m个取值的特征,经过独热编码处理后,转为m个二元特征(值只有0和1),每次只有一个激活。 基于树的方法是不需要进行特征的归一化,例如随机森林,bagging 和 boosting等。基于参数的模型或基于距离的模型,都是要进行特征的归一化。 @author: soyo \'\'\' import pandas as pd import numpy import matplotlib.pylab as pl from sklearn.linear_model import LogisticRegression from sklearn.cross_validation import train_test_split from sklearn.utils.extmath import cartesian #numpy.set_printoptions(threshold=numpy.inf) #目的是将print省略的部分都输出 data=pd.read_csv("/home/soyo/文档/LogisticRegression.csv") print data print data.head(5) data_dum=pd.get_dummies(data,prefix=\'rank\',columns=[\'rank\'],drop_first=True) #类别型变量进行独热编码,drop_first=True:删掉了本该有的rank_1 print data_dum.head(5) print "*********************" print data_dum.ix[:,1:].head(5) print data_dum.ix[:,0].head(5) x_train,x_test,y_train,y_test=train_test_split(data_dum.ix[:,1:],data_dum.ix[:,0],test_size=0.1,random_state=1) #x:代表的是数据特征,y:代表的是类标(lable),都被随机的拆分开做交叉验证 print len(x_train),len(x_test) print x_train numpy.savetxt(\'/home/soyo/文档/new.csv\', x_train,fmt="%d", delimiter = \',\') print len(y_train),len(y_test) numpy.savetxt(\'/home/soyo/文档/new2.csv\', y_train,fmt="%d", delimiter = \',\') print y_train print "***********" print y_test lr=LogisticRegression() lr.fit(x_train,y_train) print "预测结果:" print lr.predict(x_test) print "真实label:" print numpy.array(y_test) print "逻辑回归的准确率为:{0:.3f}%".format(lr.score(x_test, y_test)) print "根据组合数据分析数据之间的关系" gres=numpy.linspace(data[\'gre\'].min(),data[\'gre\'].max(),20) print gres gpas=numpy.linspace(data[\'gpa\'].min(),data[\'gpa\'].max(),20) print gpas # numpy.set_printoptions(threshold=numpy.inf) #目的是将print省略的部分都输出 print cartesian([gres,gpas,[1,2,3,4],[1.]]) #数据组合:组合后的总个数->20*20*4*1=1600个 data_new=pd.DataFrame(cartesian([gres,gpas,[1,2,3,4],[1.]])) print data_new data_new.columns=[\'gre\',\'gpa\',\'ranks\',\'intercept\'] print data_new dummy_ranks=pd.get_dummies(data_new[\'ranks\'],prefix=\'ranks\') #prefix:前缀名 # print dummy_ranks dummy_ranks.columns=[\'ranks_1\',\'ranks_2\',\'ranks_3\',\'ranks_4\'] print dummy_ranks cols_to_keep=[\'gre\',\'gpa\'] cobs=data_new[cols_to_keep].join(dummy_ranks.ix[:,\'ranks_2\':]) print "*********6" print cobs print lr.predict(cobs) data_new[\'predict_admit\']=lr.predict(cobs) # data_new[\'predict_admit\']=numpy.linspace(5,100,1600) print data_new grouped=pd.pivot_table(data_new,values=[\'predict_admit\'],index=[\'gre\',\'ranks\'],aggfunc=numpy.mean) print grouped print "*********9" print grouped.index.get_level_values(1) print grouped.ix[grouped.index.get_level_values(1)==2].index.get_level_values(0) def target_plot(x): grouped=pd.pivot_table(data_new,values=[\'predict_admit\'],index=[x,\'ranks\'],aggfunc=numpy.mean) #pivot_table:数据透视表->为了聚合统计数据 colors=\'rbgyrbgy\' for col in data_new.ranks.unique(): plt_data=grouped.ix[grouped.index.get_level_values(1)==col] pl.plot(plt_data.index.get_level_values(0),plt_data[\'predict_admit\'],color=colors[int(col)]) pl.xlabel(x) pl.ylabel("P(admit=1") pl.legend([\'1\',\'2\',\'3\',\'4\'],loc=\'upper left\',title=\'ranks\') pl.title("soyo") pl.show() target_plot(\'gpa\')
结果:
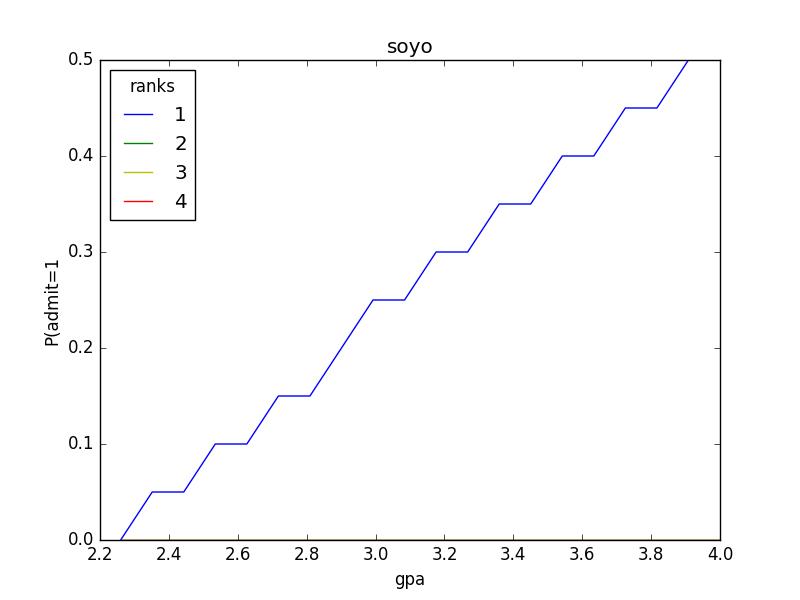
admit gre gpa rank 0 0 380 3.61 3 1 1 660 3.67 3 2 1 800 4.00 1 3 1 640 3.19 4 4 0 520 2.93 4 5 1 760 3.00 2 6 1 560 2.98 1 7 0 400 3.08 2 8 1 540 3.39 3 9 0 700 3.92 2 10 0 800 4.00 4 11 0 440 3.22 1 12 1 760 4.00 1 13 0 700 3.08 2 14 1 700 4.00 1 15 0 480 3.44 3 16 0 780 3.87 4 17 0 360 2.56 3 18 0 800 3.75 2 19 1 540 3.81 1 20 0 500 3.17 3 21 1 660 3.63 2 22 0 600 2.82 4 23 0 680 3.19 4 24 1 760 3.35 2 25 1 800 3.66 1 26 1 620 3.61 1 27 1 520 3.74 4 28 1 780 3.22 2 29 0 520 3.29 1 .. ... ... ... ... 370 1 540 3.77 2 371 1 680 3.76 3 372 1 680 2.42 1 373 1 620 3.37 1 374 0 560 3.78 2 375 0 560 3.49 4 376 0 620 3.63 2 377 1 800 4.00 2 378 0 640 3.12 3 379 0 540 2.70 2 380 0 700 3.65 2 381 1 540 3.49 2 382 0 540 3.51 2 383 0 660 4.00 1 384 1 480 2.62 2 385 0 420 3.02 1 386 1 740 3.86 2 387 0 580 3.36 2 388 0 640 3.17 2 389 0 640 3.51 2 390 1 800 3.05 2 391 1 660 3.88 2 392 1 600 3.38 3 393 1 620 3.75 2 394 1 460 3.99 3 395 0 620 4.00 2 396 0 560 3.04 3 397 0 460 2.63 2 398 0 700 3.65 2 399 0 600 3.89 3 [400 rows x 4 columns] admit gre gpa rank 0 0 380 3.61 3 1 1 660 3.67 3 2 1 800 4.00 1 3 1 640 3.19 4 4 0 520 2.93 4 admit gre gpa rank_2 rank_3 rank_4 0 0 380 3.61 0.0 1.0 0.0 1 1 660 3.67 0.0 1.0 0.0 2 1 800 4.00 0.0 0.0 0.0 3 1 640 3.19 0.0 0.0 1.0 4 0 520 2.93 0.0 0.0 1.0 ********************* gre gpa rank_2 rank_3 rank_4 0 380 3.61 0.0 1.0 0.0 1 660 3.67 0.0 1.0 0.0 2 800 4.00 0.0 0.0 0.0 3 640 3.19 0.0 0.0 1.0 4 520 2.93 0.0 0.0 1.0 0 0 1 1 2 1 3 1 4 0 Name: admit, dtype: int64 360 40 gre gpa rank_2 rank_3 rank_4 268 680 3.46 1.0 0.0 0.0 204 600 3.89 0.0 0.0 0.0 171 540 2.81 0.0 1.0 0.0 62 640 3.67 0.0 1.0 0.0 385 420 3.02 0.0 0.0 0.0 85 520 2.98 1.0 0.0 0.0 389 640 3.51 1.0 0.0 0.0 307 580 3.51 1.0 0.0 0.0 314 540 3.46 0.0 0.0 1.0 278 680 3.00 0.0 0.0 1.0 65 600 3.59 1.0 0.0 0.0 225 720 3.50 0.0 1.0 0.0 229 720 3.42 1.0 0.0 0.0 18 800 3.75 1.0 0.0 0.0 296 560 3.16 0.0 0.0 0.0 286 800 3.22 0.0 0.0 0.0 272 680 3.67 1.0 0.0 0.0 117 700 3.72 1.0 0.0 0.0 258 520 3.51 1.0 0.0 0.0 360 520 4.00 0.0 0.0 0.0 107 480 3.13 1.0 0.0 0.0 67 620 3.30 0.0 0.0 0.0 234 800 3.53 0.0 0.0 0.0 246 680 3.34 1.0 0.0 0.0 354 540 3.78 1.0 0.0 0.0 222 480 3.02 0.0 0.0 0.0 106 700 3.56 0.0 0.0 0.0 310 560 4.00 0.0 1.0 0.0 270 640 3.95 1.0 0.0 0.0 312 660 3.77 0.0 1.0 0.0 .. ... ... ... ... ... 317 780 3.63 0.0 0.0 1.0 319 540 3.28 0.0 0.0 0.0 7 400 3.08 1.0 0.0 0.0 141 700 3.52 0.0 0.0 1.0 86 600 3.32 1.0 0.0 0.0 352 580 3.12 0.0 1.0 0.0 241 520 3.81 0.0 0.0 0.0 215 660 2.91 0.0 1.0 0.0 68 580 3.69 0.0 0.0 0.0 50 640 3.86 0.0 1.0 0.0 156 560 2.52 1.0 0.0 0.0 252 520 4.00 1.0 0.0 0.0 357 720 3.31 0.0 0.0 0.0 254 740 3.52 0.0 0.0 1.0 276 460 3.77 0.0 1.0 0.0 178 620 3.33 0.0 1.0 0.0 281 360 3.27 0.0 1.0 0.0 237 480 4.00 1.0 0.0 0.0 71 300 2.92 0.0 0.0 1.0 129 460 3.15 0.0 0.0 1.0 144 580 3.40 0.0 0.0 1.0 335 620 3.71 0.0 0.0 0.0 133 500 3.08 0.0 1.0 0.0 203 420 3.92 0.0 0.0 1.0 393 620 3.75 1.0 0.0 0.0 255 640 3.35 0.0 1.0 0.0 72 480 3.39 0.0 0.0 1.0 396 560 3.04 0.0 1.0 0.0 235 620 3.05 1.0 0.0 0.0 37 520 2.90 0.0 1.0 0.0 [360 rows x 5 columns] 360 40 268 1 204 1 171 0 62 0 385 0 85 0 389 0 307 0 314 0 278 1 65 0 225 1 229 1 18 0 296 0 286 1 272 1 117 0 258 0 360 1 107 0 67 0 234 1 246 0 354 1 222 1 106 1 310 0 270 1 312 0 .. 317 1 319 0 7 0 141 1 86 0 352 1 241 1 215 1 68 0 50 0 156 0 252 1 357 0 254 1 276 0 178 0 281 0 237 0 71 0 129 0 144 0 335 1 133 0 203 0 393 1 255 0 72 0 396 0 235 0 37 0 Name: admit, dtype: int64 *********** 398 0 125 0 328 0 339 1 172 0 342 0 197 1 291 0 29 0 284 1 174 0 372 1 188 0 324 0 321 0 227 0 371 1 5 1 78 0 223 0 122 0 242 1 382 0 214 1 17 0 92 0 366 0 201 1 361 1 207 1 81 0 4 0 165 0 275 1 6 1 80 0 58 0 102 0 397 0 139 1 Name: admit, dtype: int64 预测结果: [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 1] 真实label: [0 0 0 1 0 0 1 0 0 1 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 0 1] 逻辑回归的准确率为:0.675% 根据组合数据分析数据之间的关系 [ 220. 250.52631579 281.05263158 311.57894737 342.10526316 372.63157895 403.15789474 433.68421053 464.21052632 494.73684211 525.26315789 555.78947368 586.31578947 616.84210526 647.36842105 677.89473684 708.42105263 738.94736842 769.47368421 800. ] [ 2.26 2.35157895 2.44315789 2.53473684 2.62631579 2.71789474 2.80947368 2.90105263 2.99263158 3.08421053 3.17578947 3.26736842 3.35894737 3.45052632 3.54210526 3.63368421 3.72526316 3.81684211 3.90842105 4. ] [[ 220. 2.26 1. 1. ] [ 220. 2.26 2. 1. ] [ 220. 2.26 3. 1. ] ..., [ 800. 4. 2. 1. ] [ 800. 4. 3. 1. ] [ 800. 4. 4. 1. ]] 0 1 2 3 0 220.0 2.260000 1.0 1.0 1 220.0 2.260000 2.0 1.0 2 220.0 2.260000 3.0 1.0 3 220.0 2.260000 4.0 1.0 4 220.0 2.351579 1.0 1.0 5 220.0 2.351579 2.0 1.0 6 220.0 2.351579 3.0 1.0 7 220.0 2.351579 4.0 1.0 8 220.0 2.443158 1.0 1.0 9 220.0 2.443158 2.0 1.0 10 220.0 2.443158 3.0 1.0 11 220.0 2.443158 4.0 1.0 12 220.0 2.534737 1.0 1.0 13 220.0 2.534737 2.0 1.0 14 220.0 2.534737 3.0 1.0 15 220.0 2.534737 4.0 1.0 16 220.0 2.626316 1.0 1.0 17 220.0 2.626316 2.0 1.0 18 220.0 2.626316 3.0 1.0 19 220.0 2.626316 4.0 1.0 20 220.0 2.717895 1.0 1.0 21 220.0 2.717895 2.0 1.0 22 220.0 2.717895 3.0 1.0 23 220.0 2.717895 4.0 1.0 24 220.0 2.809474 1.0 1.0 25 220.0 2.809474 2.0 1.0 26 220.0 2.809474 3.0 1.0 27 220.0 2.809474 4.0 1.0 28 220.0 2.901053 1.0 1.0 29 220.0 2.901053 2.0 1.0 ... ... ... ... ... 1570 800.0 3.358947 3.0 1.0 1571 800.0 3.358947 4.0 1.0 1572 800.0 3.450526 1.0 1.0 1573 800.0 3.450526 2.0 1.0 1574 800.0 3.450526 3.0 1.0 1575 800.0 3.450526 4.0 1.0 1576 800.0 3.542105 1.0 1.0 1577 800.0 3.542105 2.0 1.0 1578 800.0 3.542105 3.0 1.0 1579 800.0 3.542105 4.0 1.0 1580 800.0 3.633684 1.0 1.0 1581 800.0 3.633684 2.0 1.0 1582 800.0 3.633684 3.0 1.0 1583 800.0 3.633684 4.0 1.0 1584 800.0 3.725263 1.0 1.0 1585 800.0 3.725263 2.0 1.0 1586 800.0 3.725263 3.0 1.0 1587 800.0 3.725263 4.0 1.0 1588 800.0 3.816842 1.0 1.0 1589 800.0 3.816842 2.0 1.0 1590 800.0 3.816842 3.0 1.0 1591 800.0 3.816842 4.0 1.0 1592 800.0 3.908421 1.0 1.0 1593 800.0 3.908421 2.0 1.0 1594 800.0 3.908421 3.0 1.0 1595 800.0 3.908421 4.0 1.0 1596 800.0 4.000000 1.0 1.0 1597 800.0 4.000000 2.0 1.0 1598 800.0 4.000000 3.0 1.0 1599 800.0 4.000000 4.0 1.0 [1600 rows x 4 columns] gre gpa ranks intercept 0 220.0 2.260000 1.0 1.0 1 220.0 2.260000 2.0 1.0 2 220.0 2.260000 3.0 1.0 3 220.0 2.260000 4.0 1.0 4 220.0 2.351579 1.0 1.0 5 220.0 2.351579 2.0 1.0 6 220.0 2.351579 3.0 1.0 7 220.0 2.351579 4.0 1.0 8 220.0 2.443158 1.0 1.0 9 220.0 2.443158 2.0 1.0 10 220.0 2.443158 3.0 1.0 11 220.0 2.443158 4.0 1.0 12 220.0 2.534737 1.0 1.0 13 220.0 2.534737 2.0 1.0 14 220.0 2.534737 3.0 1.0 15 220.0 2.534737 4.0 1.0 16 220.0 2.626316 1.0 1.0 17 220.0 2.626316 2.0 1.0 18 220.0 2.626316 3.0 1.0 19 220.0 2.626316 4.0 1.0 20 220.0 2.717895 1.0 1.0 21 220.0 2.717895 2.0 1.0 22 220.0 2.717895 3.0 1.0 23 220.0 2.717895 4.0 1.0 24 220.0 2.809474 1.0 1.0 25 220.0 2.809474 2.0 1.0 26 220.0 2.809474 3.0 1.0 27 220.0 2.809474 4.0 1.0 28 220.0 2.901053 1.0 1.0 29 220.0 2.901053 2.0 1.0 ... ... ... ... ... 1570 800.0 3.358947 3.0 1.0 1571 800.0 3.358947 4.0 1.0 1572 800.0 3.450526 1.0 1.0 1573 800.0 3.450526 2.0 1.0 1574 800.0 3.450526 3.0 1.0 1575 800.0 3.450526 4.0 1.0 1576 800.0 3.542105 1.0 1.0 1577 800.0 3.542105 2.0 1.0 1578 800.0 3.542105 3.0 1.0 1579 800.0 3.542105 4.0 1.0 1580 800.0 3.633684 1.0 1.0 1581 800.0 3.633684 2.0 1.0 1582 800.0 3.633684 3.0 1.0 1583 800.0 3.633684 4.0 1.0 1584 800.0 3.725263 1.0 1.0 1585 800.0 3.725263 2.0 1.0 1586 800.0 3.725263 3.0 1.0 1587 800.0 3.725263 4.0 1.0 1588 800.0 3.816842 1.0 1.0 1589 800.0 3.816842 2.0 1.0 1590 800.0 3.816842 3.0 1.0 1591 800.0 3.816842 4.0 1.0 1592 800.0 3.908421 1.0 1.0 1593 800.0 3.908421 2.0 1.0 1594 800.0 3.908421 3.0 1.0 1595 800.0 3.908421 4.0 1.0 1596 800.0 4.000000 1.0 1.0 1597 800.0 4.000000 2.0 1.0 1598 800.0 4.000000 3.0 1.0 1599 800.0 4.000000 4.0 1.0 [1600 rows x 4 columns] ranks_1 ranks_2 ranks_3 ranks_4 0 1.0 0.0 0.0 0.0 1 0.0 1.0 0.0 0.0 2 0.0 0.0 1.0 0.0 3 0.0 0.0 0.0 1.0 4 1.0 0.0 0.0 0.0 5 0.0 1.0 0.0 0.0 6 0.0 0.0 1.0 0.0 7 0.0 0.0 0.0 1.0 8 1.0 0.0 0.0 0.0 9 0.0 1.0 0.0 0.0 10 0.0 0.0 1.0 0.0 11 0.0 0.0 0.0 1.0 12 1.0 0.0 0.0 0.0 13 0.0 1.0 0.0 0.0 14 0.0 0.0 1.0 0.0 15 0.0 0.0 0.0 1.0 16 1.0 0.0 0.0 0.0 17 0.0 1.0 0.0 0.0 18 0.0 0.0 1.0 0.0 19 0.0 0.0 0.0 1.0 20 1.0 0.0 0.0 0.0 21 0.0 1.0 0.0 0.0 22 0.0 0.0 1.0 0.0 23 0.0 0.0 0.0 1.0 24 1.0 0.0 0.0 0.0 25 0.0 1.0 0.0 0.0 26 0.0 0.0 1.0 0.0 27 0.0 0.0 0.0 1.0 28 1.0 0.0 0.0 0.0 29 0.0 1.0 0.0 0.0 ... ... ... ... ... 1570 0.0 0.0 1.0 0.0 1571 0.0 0.0 0.0 1.0 1572 1.0 0.0 0.0 0.0 1573 0.0 1.0 0.0 0.0 1574 0.0 0.0 1.0 0.0 1575 0.0 0.0 0.0 1.0 1576 1.0 0.0 0.0 0.0 1577 0.0 1.0 0.0 0.0 1578 0.0 0.0 1.0 0.0 1579 0.0 0.0 0.0 1.0 1580 1.0 0.0 0.0 0.0 1581 0.0 1.0 0.0 0.0 1582 0.0 0.0 1.0 0.0 1583 0.0 0.0 0.0 1.0 1584 1.0 0.0 0.0 0.0 1585 0.0 1.0 0.0 0.0 1586 0.0 0.0 1.0 0.0 1587 0.0 0.0 0.0 1.0 1588 1.0 0.0 0.0 0.0 1589 0.0 1.0 0.0 0.0 1590 0.0 0.0 1.0 0.0 1591 0.0 0.0 0.0 1.0 1592 1.0 0.0 0.0 0.0 1593 0.0 1.0 0.0 0.0 1594 0.0 0.0 1.0 0.0 1595 0.0 0.0 0.0 1.0 1596 1.0 0.0 0.0 0.0 1597 0.0 1.0 0.0 0.0 1598 0.0 0.0 1.0 0.0 1599 0.0 0.0 0.0 1.0 [1600 rows x 4 columns] *********6 gre gpa ranks_2 ranks_3 ranks_4 0 220.0 2.260000 0.0 0.0 0.0 1 220.0 2.260000 1.0 0.0 0.0 2 220.0 2.260000 0.0 1.0 0.0 3 220.0 2.260000 0.0 0.0 1.0 4 220.0 2.351579 0.0 0.0 0.0 5 220.0 2.351579 1.0 0.0 0.0 6 220.0 2.351579 0.0 1.0 0.0 7 220.0 2.351579 0.0 0.0 1.0 8 220.0 2.443158 0.0 0.0 0.0 9 220.0 2.443158 1.0 0.0 0.0 10 220.0 2.443158 0.0 1.0 0.0 11 220.0 2.443158 0.0 0.0 1.0 12 220.0 2.534737 0.0 0.0 0.0 13 220.0 2.534737 1.0 0.0 0.0 14 220.0 2.534737 0.0 1.0 0.0 15 220.0 2.534737 0.0 0.0 1.0 16 220.0 2.626316 0.0 0.0 0.0 17 220.0 2.626316 1.0 0.0 0.0 18 220.0 2.626316 0.0 1.0 0.0 19 220.0 2.626316 0.0 0.0 1.0 20 220.0 2.717895 0.0 0.0 0.0 21 220.0 2.717895 1.0 0.0 0.0 22 220.0 2.717895 0.0 1.0 0.0 23 220.0 2.717895 0.0 0.0 1.0 24 220.0 2.809474 0.0 0.0 0.0 25 220.0 2.809474 1.0 0.0 0.0 26 220.0 2.809474 0.0 1.0 0.0 27 220.0 2.809474 0.0 0.0 1.0 28 220.0 2.901053 0.0 0.0 0.0 29 220.0 2.901053 1.0 0.0 0.0 ... ... ... ... ... ... 1570 800.0 3.358947 0.0 1.0 0.0 1571 800.0 3.358947 0.0 0.0 1.0 1572 800.0 3.450526 0.0 0.0 0.0 1573 800.0 3.450526 1.0 0.0 0.0 1574 800.0 3.450526 0.0 1.0 0.0 1575 800.0 3.450526 0.0 0.0 1.0 1576 800.0 3.542105 0.0 0.0 0.0 1577 800.0 3.542105 1.0 0.0 0.0 1578 800.0 3.542105 0.0 1.0 0.0 1579 800.0 3.542105 0.0 0.0 1.0 1580 800.0 3.633684 0.0 0.0 0.0 1581 800.0 3.633684 1.0 0.0 0.0 1582 800.0 3.633684 0.0 1.0 0.0 1583 800.0 3.633684 0.0 0.0 1.0 1584 800.0 3.725263 0.0 0.0 0.0 1585 800.0 3.725263 1.0 0.0 0.0 1586 800.0 3.725263 0.0 1.0 0.0 1587 800.0 3.725263 0.0 0.0 1.0 1588 800.0 3.816842 0.0 0.0 0.0 1589 800.0 3.816842 1.0 0.0 0.0 1590 800.0 3.816842 0.0 1.0 0.0 1591 800.0 3.816842 0.0 0.0 1.0 1592 800.0 3.908421 0.0 0.0 0.0 1593 800.0 3.908421 1.0 0.0 0.0 1594 800.0 3.908421 0.0 1.0 0.0 1595 800.0 3.908421 0.0 0.0 1.0 1596 800.0 4.000000 0.0 0.0 0.0 1597 800.0 4.000000 1.0 0.0 0.0 1598 800.0 4.000000 0.0 1.0 0.0 1599 800.0 4.000000 0.0 0.0 1.0 [1600 rows x 5 columns] [0 0 0 ..., 0 0 0] gre gpa ranks intercept predict_admit 0 220.0 2.260000 1.0 1.0 0 1 220.0 2.260000 2.0 1.0 0 2 220.0 2.260000 3.0 1.0 0 3 220.0 2.260000 4.0 1.0 0 4 220.0 2.351579 1.0 1.0 0 5 220.0 2.351579 2.0 1.0 0 6 220.0 2.351579 3.0 1.0 0 7 220.0 2.351579 4.0 1.0 0 8 220.0 2.443158 1.0 1.0 0 9 220.0 2.443158 2.0 1.0 0 10 220.0 2.443158 3.0 1.0 0 11 220.0 2.443158 4.0 1.0 0 12 220.0 2.534737 1.0 1.0 0 13 220.0 2.534737 2.0 1.0 0 14 220.0 2.534737 3.0 1.0 0 15 220.0 2.534737 4.0 1.0 0 16 220.0 2.626316 1.0 1.0 0 17 220.0 2.626316 2.0 1.0 0 18 220.0 2.626316 3.0 1.0 0 19 220.0 2.626316 4.0 1.0 0 20 220.0 2.717895 1.0 1.0 0 21 220.0 2.717895 2.0 1.0 0 22 220.0 2.717895 3.0 1.0 0 23 220.0 2.717895 4.0 1.0 0 24 220.0 2.809474 1.0 1.0 0 25 220.0 2.809474 2.0 1.0 0 26 220.0 2.809474 3.0 1.0 0 27 220.0 2.809474 4.0 1.0 0 28 220.0 2.901053 1.0 1.0 0 29 220.0 2.901053 2.0 1.0 0 ... ... ... ... ... ... 1570 800.0 3.358947 3.0 1.0 0 1571 800.0 3.358947 4.0 1.0 0 1572 800.0 3.450526 1.0 1.0 1 1573 800.0 3.450526 2.0 1.0 0 1574 800.0 3.450526 3.0 1.0 0 1575 800.0 3.450526 4.0 1.0 0 1576 800.0 3.542105 1.0 1.0 1 1577 800.0 3.542105 2.0 1.0 0 1578 800.0 3.542105 3.0 1.0 0 1579 800.0 3.542105 4.0 1.0 0 1580 800.0 3.633684 1.0 1.0 1 1581 800.0 3.633684 2.0 1.0 0 1582 800.0 3.633684 3.0 1.0 0 1583 800.0 3.633684 4.0 1.0 0 1584 800.0 3.725263 1.0 1.0 1 1585 800.0 3.725263 2.0 1.0 0 1586 800.0 3.725263 3.0 1.0 0 1587 800.0 3.725263 4.0 1.0 0 1588 800.0 3.816842 1.0 1.0 1 1589 800.0 3.816842 2.0 1.0 0 1590 800.0 3.816842 3.0 1.0 0 1591 800.0 3.816842 4.0 1.0 0 1592 800.0 3.908421 1.0 1.0 1 1593 800.0 3.908421 2.0 1.0 0 1594 800.0 3.908421 3.0 1.0 0 1595 800.0 3.908421 4.0 1.0 0 1596 800.0 4.000000 1.0 1.0 1 1597 800.0 4.000000 2.0 1.0 0 1598 800.0 4.000000 3.0 1.0 0 1599 800.0 4.000000 4.0 1.0 0 [1600 rows x 5 columns] predict_admit gre ranks 220.000000 1.0 0.00 2.0 0.00 3.0 0.00 4.0 0.00 250.526316 1.0 0.00 2.0 0.00 3.0 0.00 4.0 0.00 281.052632 1.0 0.00 2.0 0.00 3.0 0.00 4.0 0.00 311.578947 1.0 0.00 2.0 0.00 3.0 0.00 4.0 0.00 342.105263 1.0 0.00 2.0 0.00 3.0 0.00 4.0 0.00 372.631579 1.0 0.00 2.0 0.00 3.0 0.00 4.0 0.00 403.157895 1.0 0.00 2.0 0.00 3.0 0.00 4.0 0.00 433.684211 1.0 0.00 2.0 0.00 ... ... 586.315789 3.0 0.00 4.0 0.00 616.842105 1.0 0.40 2.0 0.00 3.0 0.00 4.0 0.00 647.368421 1.0 0.50 2.0 0.00 3.0 0.00 4.0 0.00 677.894737 1.0 0.60 2.0 0.00 3.0 0.00 4.0 0.00 708.421053 1.0 0.65 2.0 0.00 3.0 0.00 4.0 0.00 738.947368 1.0 0.75 2.0 0.00 3.0 0.00 4.0 0.00 769.473684 1.0 0.85 2.0 0.00 3.0 0.00 4.0 0.00 800.000000 1.0 0.95 2.0 0.00 3.0 0.00 4.0 0.00 [80 rows x 1 columns] *********9 Float64Index([1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0, 4.0], dtype=\'float64\', name=u\'ranks\') Float64Index([ 220.0, 250.526315789, 281.052631579, 311.578947368, 342.105263158, 372.631578947, 403.157894737, 433.684210526, 464.210526316, 494.736842105, 525.263157895, 555.789473684, 586.315789474, 616.842105263, 647.368421053, 677.894736842, 708.421052632, 738.947368421, 769.473684211, 800.0], dtype=\'float64\', name=u\'gre\')
以上是关于逻辑回归--数据独热编码+数据结果可视化的主要内容,如果未能解决你的问题,请参考以下文章