逻辑回归--参数解释＋数据特征不独热编码＋训练数据分布可视话
Posted soyosuyang
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了逻辑回归--参数解释＋数据特征不独热编码＋训练数据分布可视话相关的知识，希望对你有一定的参考价值。
#-*- coding: utf-8 -*- \'\'\' 逻辑回归参数： penalty：惩罚项，str类型，可选参数为l1和l2，默认为l2。用于指定惩罚项中使用的规范。newton-cg、sag和lbfgs求解算法只支持L2规范。L1G规范假设的是模型的参数满足拉普拉斯分布，L2假设的模型参数满足高斯分布，所谓的范式就是加上对参数的约束，使得模型更不会过拟合(overfit)，但是如果要说是不是加了约束就会好，这个没有人能回答，只能说，加约束的情况下，理论上应该可以获得泛化能力更强的结果。 dual：对偶或原始方法，bool类型，默认为False。对偶方法只用在求解线性多核(liblinear)的L2惩罚项上。当样本数量>样本特征的时候，dual通常设置为False。 tol：停止求解的标准，float类型，默认为1e-4。就是求解到多少的时候，停止，认为已经求出最优解。 c：正则化系数λ的倒数，float类型，默认为1.0。必须是正浮点型数。像SVM一样，越小的数值表示越强的正则化。 fit_intercept：是否存在截距或偏差，bool类型，默认为True。 intercept_scaling：仅在正则化项为”liblinear”，且fit_intercept设置为True时有用。float类型，默认为1。 class_weight：用于标示分类模型中各种类型的权重，可以是一个字典或者’balanced’字符串，默认为不输入，也就是不考虑权重，即为None。如果选择输入的话，可以选择balanced让类库自己计算类型权重，或者自己输入各个类型的权重。举个例子，比如对于0,1的二元模型，我们可以定义class_weight={0:0.9,1:0.1}，这样类型0的权重为90%，而类型1的权重为10%。如果class_weight选择balanced，那么类库会根据训练样本量来计算权重。某种类型样本量越多，则权重越低，样本量越少，则权重越高。当class_weight为balanced时，类权重计算方法如下：n_samples / (n_classes * np.bincount(y))。n_samples为样本数，n_classes为类别数量，np.bincount(y)会输出每个类的样本数，例如y=[1,0,0,1,1],则np.bincount(y)=[2,3]。 random_state：随机数种子，int类型，可选参数，默认为无，仅在正则化优化算法为sag,liblinear时有用。 solver：优化算法选择参数，只有五个可选参数，即newton-cg,lbfgs,liblinear,sag,saga。默认为liblinear。solver参数决定了我们对逻辑回归损失函数的优化方法，有四种算法可以选择，分别是： liblinear：使用了开源的liblinear库实现，内部使用了坐标轴下降法来迭代优化损失函数。 lbfgs：拟牛顿法的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。 newton-cg：也是牛顿法家族的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。 sag：即随机平均梯度下降，是梯度下降法的变种，和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度，适合于样本数据多的时候。 saga：线性收敛的随机优化算法的的变重。 @author: soyo \'\'\' import pandas as pd import numpy import matplotlib.pylab as plt from sklearn.linear_model import LogisticRegression from sklearn.cross_validation import train_test_split from sklearn.utils.extmath import cartesian data=pd.read_csv("/home/soyo/文档/LogisticRegression.csv") #data是DF print data print data.head(5) # data["gre"].hist(color="red") data.hist(color="red") plt.show() print data.describe() # describe：给出数据的基本统计信息。std:标准差 print "******************1" print pd.crosstab(data[\'admit\'], data[\'rank\'],rownames=[\'admit\']) # print pd.crosstab(data[\'rank\'], data[\'admit\'],rownames=[\'rank\']) #也ok print "***************2" x_train,x_test,y_train,y_test=train_test_split(data.ix[:,1:],data.ix[:,0],test_size=0.1,random_state=1) #x:代表的是数据特征，y:代表的是类标(lable)，都被随机的拆分开做交叉验证 print len(x_train),len(x_test) print x_train print y_train print "***********3" print y_test lr=LogisticRegression(C=0.2) #不用独热编码，分类的准确率不变，C的降低提高了准确率 lr.fit(x_train,y_train) print "预测结果：" print lr.predict(x_test) print "真实label:" print numpy.array(y_test) print "逻辑回归的准确率为:{0:.3f}%".format(lr.score(x_test, y_test))
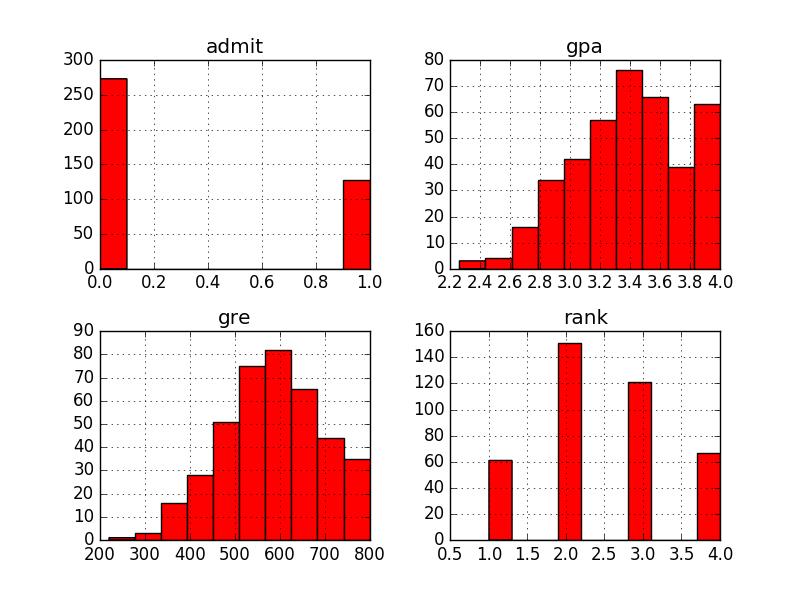
admit gre gpa rank 0 0 380 3.61 3 1 1 660 3.67 3 2 1 800 4.00 1 3 1 640 3.19 4 4 0 520 2.93 4 5 1 760 3.00 2 6 1 560 2.98 1 7 0 400 3.08 2 8 1 540 3.39 3 9 0 700 3.92 2 10 0 800 4.00 4 11 0 440 3.22 1 12 1 760 4.00 1 13 0 700 3.08 2 14 1 700 4.00 1 15 0 480 3.44 3 16 0 780 3.87 4 17 0 360 2.56 3 18 0 800 3.75 2 19 1 540 3.81 1 20 0 500 3.17 3 21 1 660 3.63 2 22 0 600 2.82 4 23 0 680 3.19 4 24 1 760 3.35 2 25 1 800 3.66 1 26 1 620 3.61 1 27 1 520 3.74 4 28 1 780 3.22 2 29 0 520 3.29 1 .. ... ... ... ... 370 1 540 3.77 2 371 1 680 3.76 3 372 1 680 2.42 1 373 1 620 3.37 1 374 0 560 3.78 2 375 0 560 3.49 4 376 0 620 3.63 2 377 1 800 4.00 2 378 0 640 3.12 3 379 0 540 2.70 2 380 0 700 3.65 2 381 1 540 3.49 2 382 0 540 3.51 2 383 0 660 4.00 1 384 1 480 2.62 2 385 0 420 3.02 1 386 1 740 3.86 2 387 0 580 3.36 2 388 0 640 3.17 2 389 0 640 3.51 2 390 1 800 3.05 2 391 1 660 3.88 2 392 1 600 3.38 3 393 1 620 3.75 2 394 1 460 3.99 3 395 0 620 4.00 2 396 0 560 3.04 3 397 0 460 2.63 2 398 0 700 3.65 2 399 0 600 3.89 3 [400 rows x 4 columns] admit gre gpa rank 0 0 380 3.61 3 1 1 660 3.67 3 2 1 800 4.00 1 3 1 640 3.19 4 4 0 520 2.93 4 admit gre gpa rank count 400.000000 400.000000 400.000000 400.00000 mean 0.317500 587.700000 3.389900 2.48500 std 0.466087 115.516536 0.380567 0.94446 min 0.000000 220.000000 2.260000 1.00000 25% 0.000000 520.000000 3.130000 2.00000 50% 0.000000 580.000000 3.395000 2.00000 75% 1.000000 660.000000 3.670000 3.00000 max 1.000000 800.000000 4.000000 4.00000 ******************1 rank 1 2 3 4 admit 0 28 97 93 55 1 33 54 28 12 ***************2 360 40 gre gpa rank 268 680 3.46 2 204 600 3.89 1 171 540 2.81 3 62 640 3.67 3 385 420 3.02 1 85 520 2.98 2 389 640 3.51 2 307 580 3.51 2 314 540 3.46 4 278 680 3.00 4 65 600 3.59 2 225 720 3.50 3 229 720 3.42 2 18 800 3.75 2 296 560 3.16 1 286 800 3.22 1 272 680 3.67 2 117 700 3.72 2 258 520 3.51 2 360 520 4.00 1 107 480 3.13 2 67 620 3.30 1 234 800 3.53 1 246 680 3.34 2 354 540 3.78 2 222 480 3.02 1 106 700 3.56 1 310 560 4.00 3 270 640 3.95 2 312 660 3.77 3 .. ... ... ... 317 780 3.63 4 319 540 3.28 1 7 400 3.08 2 141 700 3.52 4 86 600 3.32 2 352 580 3.12 3 241 520 3.81 1 215 660 2.91 3 68 580 3.69 1 50 640 3.86 3 156 560 2.52 2 252 520 4.00 2 357 720 3.31 1 254 740 3.52 4 276 460 3.77 3 178 620 3.33 3 281 360 3.27 3 237 480 4.00 2 71 300 2.92 4 129 460 3.15 4 144 580 3.40 4 335 620 3.71 1 133 500 3.08 3 203 420 3.92 4 393 620 3.75 2 255 640 3.35 3 72 480 3.39 4 396 560 3.04 3 235 620 3.05 2 37 520 2.90 3 [360 rows x 3 columns] 268 1 204 1 171 0 62 0 385 0 85 0 389 0 307 0 314 0 278 1 65 0 225 1 229 1 18 0 296 0 286 1 272 1 117 0 258 0 360 1 107 0 67 0 234 1 246 0 354 1 222 1 106 1 310 0 270 1 312 0 .. 317 1 319 0 7 0 141 1 86 0 352 1 241 1 215 1 68 0 50 0 156 0 252 1 357 0 254 1 276 0 178 0 281 0 237 0 71 0 129 0 144 0 335 1 133 0 203 0 393 1 255 0 72 0 396 0 235 0 37 0 Name: admit, dtype: int64 ***********3 398 0 125 0 328 0 339 1 172 0 342 0 197 1 291 0 29 0 284 1 174 0 372 1 188 0 324 0 321 0 227 0 371 1 5 1 78 0 223 0 122 0 242 1 382 0 214 1 17 0 92 0 366 0 201 1 361 1 207 1 81 0 4 0 165 0 275 1 6 1 80 0 58 0 102 0 397 0 139 1 Name: admit, dtype: int64 预测结果： [0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 0 0 1] 真实label: [0 0 0 1 0 0 1 0 0 1 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 0 1] 逻辑回归的准确率为:0.750%
以上是关于逻辑回归--参数解释＋数据特征不独热编码＋训练数据分布可视话的主要内容，如果未能解决你的问题，请参考以下文章
R语言构建xgboost模型：使用xgboost模型训练tweedie回归模型，特征工程（dataframe转化到data.table独热编码缺失值删除DMatrix结构生成）
集成学习模型（xgboostlightgbmcatboost）进行回归预测构建实战：异常数据处理缺失值处理数据重采样resample独热编码预测特征检查特征可视化预测结构可视化模型