SVM 推导
点到平面的距离(几何距离):
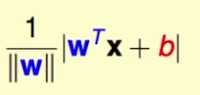
函数距离: |wx+b|,不考虑1/||w||.
SVM的优化目标:所有样本点到分离超平面的最小的几何距离最大,可以写成:
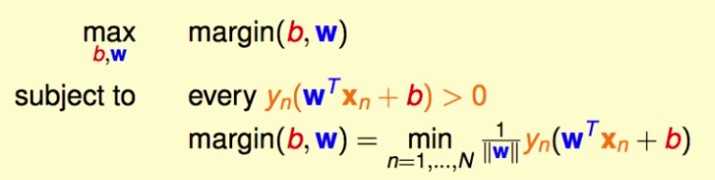
这里 限制条件的第一行表示每个样本点都被正确的分类, 第二行表示最大化的目标是样本点到分离超平面的最小几何距离。
W,b同步放缩并不影响分离超平面,故放缩至一定比例,使所有样本点到超平面的最小函数距离刚好为1, 那么最大化的目标就很简单了

需要优化的问题的形式为:
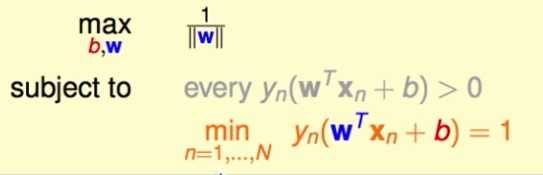
注意,既然放缩时使最小的函数间隔为1,那么实际上产生了一个比之前每个点到平面距离都>0(要分类正确)更强的条件,故之前的条件可以不要。
现在,优化问题的限制条件为最小的那一个等于1,这个比较不好解,可以对这个条件放松(所有的都>=1),使得问题更好解,但是保证最优解仍然落在=1的范围里,这样虽然放松了条件,但是最优解仍然落在之前严格条件的范围里,故最优解不变。
证明(反证法:假设最优解落在>=1,但不是=1的范围里,那么可以对最优解除以其最小值,构造一个更好的解,从而形成矛盾)

现在,需要优化的问题的形式为:
(对1 / ||w|| 做一点等价的变形)
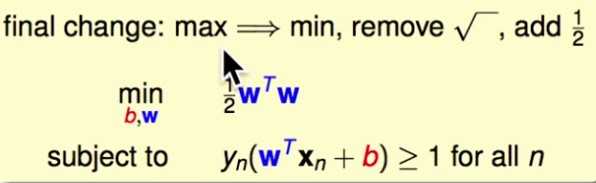
为什么更大的几何间隔更好?
(1)直观理解: 可以忍受更大的数据的噪音
(2) 考虑 对比SVM 和 带正则项的 分类器(例如logistic regression):

可以发现,这相当于E_in 和 WTW 对调了一下。
因此,SVM可以类似于带了正则项的一个模型。
(3) 从VC_dimension的复杂度层面分析,SVM降低了复杂度
例如,不加分割面的margin限制,例如PLA, 那么对于下面的样本点可能有4中分割方法;但是,如果要求分割面的margin为最小1.126,那么其实就少于4种分割方法了。因此,加上margin的限制降低了VC dimension,亦即降低了模型的复杂度。(因此SVM在vc dimension上复杂度其实比感知机低)
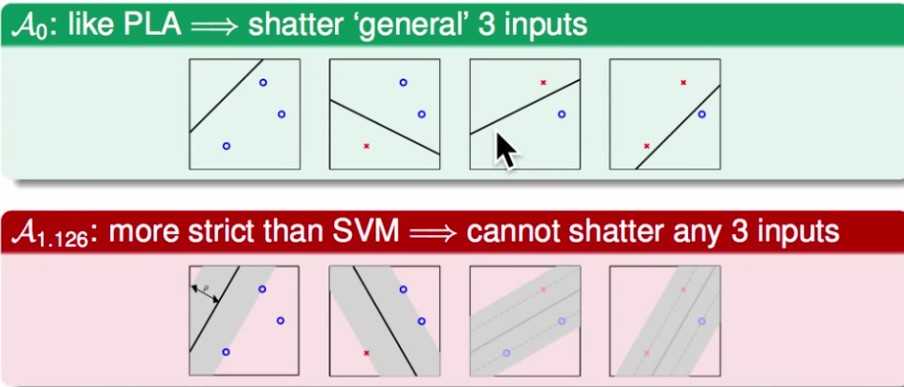
dual SVM 推导
为什么要推导dual SVM:引入核函数,使得可以在低维空间做运算,完成在高维空间的上的分类。
如果用一般的SVM(或者其他的模型),如果特征有d维(设原来的空间叫X空间),将其转换到q维空间(转换后的空间叫Z空间),那么转换后特征的维度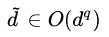 ,如果直接在Z空间训练分类器,这将大大地增加计算量;dual SVM以及核函数的目标是:无论将特征转换到多少维(甚至无限维,高斯核),都能在不变的维度(N维)下完成计算。 即转换后的模型复杂度只与N相关,而与d不相关。
,如果直接在Z空间训练分类器,这将大大地增加计算量;dual SVM以及核函数的目标是:无论将特征转换到多少维(甚至无限维,高斯核),都能在不变的维度(N维)下完成计算。 即转换后的模型复杂度只与N相关,而与d不相关。
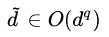 ,如果直接在Z空间训练分类器,这将大大地增加计算量;dual SVM以及核函数的目标是:无论将特征转换到多少维(甚至无限维,高斯核),都能在不变的维度(N维)下完成计算。 即转换后的模型复杂度只与N相关,而与d不相关。
,如果直接在Z空间训练分类器,这将大大地增加计算量;dual SVM以及核函数的目标是:无论将特征转换到多少维(甚至无限维,高斯核),都能在不变的维度(N维)下完成计算。 即转换后的模型复杂度只与N相关,而与d不相关。
下面推导中的Z就是X,代表样本X映射到高维空间中的结果。推导结束就会发现,W可以用Z的和的形式求解出来。
dual SVM是带条件(而且还是带不等式条件,因此涉及到KKT条件)最优化问题,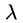 被当做是要求解的变量,而将约束转化成其他形式。
被当做是要求解的变量,而将约束转化成其他形式。
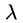 被当做是要求解的变量,而将约束转化成其他形式。
被当做是要求解的变量,而将约束转化成其他形式。假设样本数目为N,那么SVM就有N个限制条件,因此从dual SVM就有N个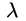 需要求解。
需要求解。
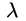 需要求解。
需要求解。定义 拉格朗日函数:

现在证明SVM等价于这个 拉格朗日函数 在所有拉格朗日乘子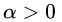 时的最小最大问题,先对
时的最小最大问题,先对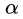 求最大(得到
求最大(得到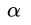 是关于b,w的函数,当再把b,w确定了,
是关于b,w的函数,当再把b,w确定了,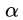 就可以求出来了
就可以求出来了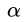 )。
)。
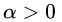 时的最小最大问题,先对
时的最小最大问题,先对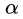 求最大(得到
求最大(得到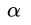 是关于b,w的函数,当再把b,w确定了,
是关于b,w的函数,当再把b,w确定了,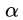 就可以求出来了
就可以求出来了),再对b,w求最小(此时式子中包含用b,w表示的
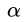 )。
)。注意两个问题都是最优化问题,因此要证明它们等价,只需要证明它们的最优解的位置是一样的。如果拉格朗日问题的最优解,也是原始SVM问题的最优解,那么它们就是等价的。(对于最优化问题,只要最优解不变,随便怎么修改原来的函数,最后都是和原来的函数等价的)
如果b,w落在符合限制条件的范围内,里面的最大化问题的值就是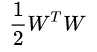 ,最后是对
,最后是对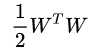 求最小。
求最小。
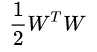 ,最后是对
,最后是对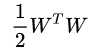 求最小。
求最小。如果b,w落在符合限制条件的范围外,里面的最大化问题的值就是无穷大,最后是对无穷大求最小
因此,可以肯定的是,拉格朗日问题的最优解(不管要怎么得出,但是可以确定它的位置属于哪个区域),还是会在符合限制条件的范围内,对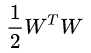 求最小得到的,因而和原来的SVM问题等价。
求最小得到的,因而和原来的SVM问题等价。
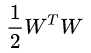 求最小得到的,因而和原来的SVM问题等价。
求最小得到的,因而和原来的SVM问题等价。
再想办法将最小最大问题转化为其对偶的最大最小问题,亦即拉格朗日对偶问题:
考虑最小最大问题,对任意一个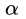 ,该不等式成立:
,该不等式成立:
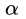 ,该不等式成立:
,该不等式成立:即不考虑里面的max动作,随便选择一个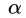 。注意,该不等式对所有的
。注意,该不等式对所有的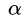 成立。
成立。
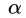 。注意,该不等式对所有的
。注意,该不等式对所有的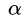 成立。
成立。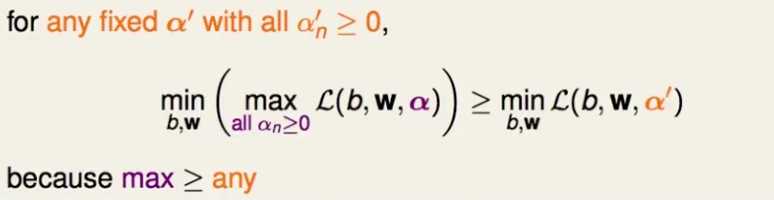
即然右边这个式子在取任意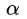 的值得时候都小于等于左边的式子,那么对它对
的值得时候都小于等于左边的式子,那么对它对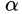 求最大值,依然小于等于左边的式子,因而,有下述的不等式:
求最大值,依然小于等于左边的式子,因而,有下述的不等式:
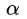 的值得时候都小于等于左边的式子,那么对它对
的值得时候都小于等于左边的式子,那么对它对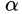 求最大值,依然小于等于左边的式子,因而,有下述的不等式:
求最大值,依然小于等于左边的式子,因而,有下述的不等式: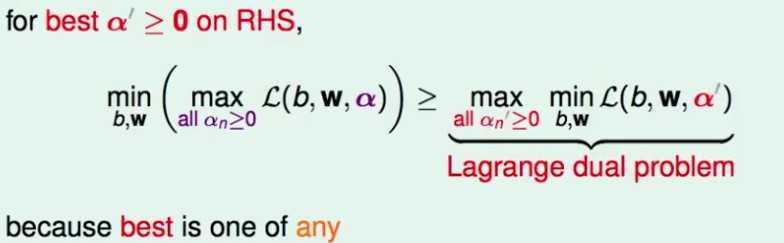
右边这个式子的里面的最小化是没有约束的,因而更容易求解。
注意这里依然是不等关系,被称之为弱对偶性;
如果是等于关系,那么被称之为强对偶性。
如果满足强对偶关系的一些条件,那么两边的问题的最优解是一样的。
什么时候对偶问题和原问题是强对偶关系呢,对于二次规划问题,如果满足以下条件,那么就是强对偶关系:
1) 凸问题
2) 原问题是有解的
3) 约束条件是线性的


可见对于dual SVM而言,对偶问题和原问题是强对偶的。即可以通过解对偶问题,得到原问题的最优解。
解对偶问题:
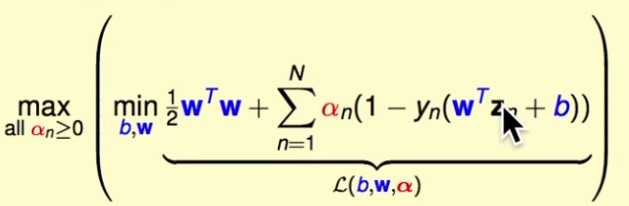
里面的问题没有限制条件,直接 偏导数=0。
先对b求偏导数,得到取得最大值时的一个约束条件:
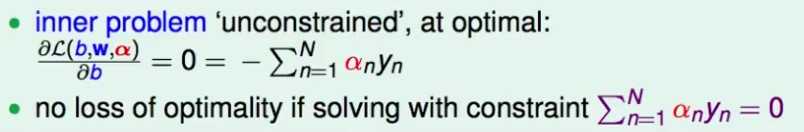
既然取得最大值时一定要满足这个约束条件,那么直接带着这个约束条件去求最大值,并不影响求解。
因为这个约束条件是一个关于b的等式,因而,将它也添加到最优化问题的约束条件里去,就可以消掉b了:
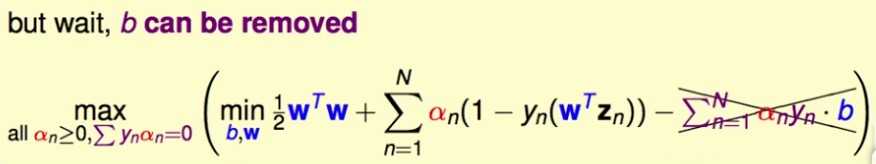
消掉b之后,之前的对b,w求最小,也就变成了对w求最小了。
再对w求偏导数:

这个约束条件是一个关于w的等式,同理,将它也直接加到原问题的约束条件里,就可以消掉问题里的w了:
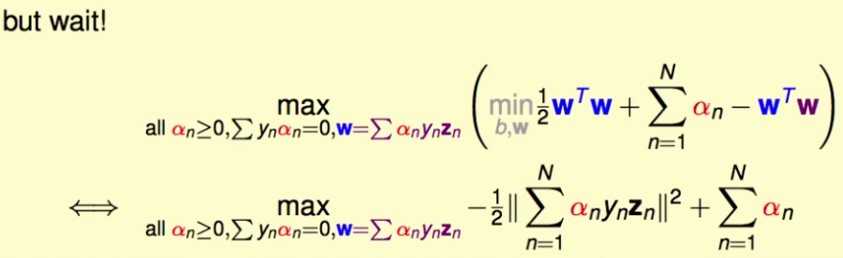
最后,优化的目标函数里只剩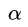 了!现在成了一个带约束的,变量只有
了!现在成了一个带约束的,变量只有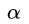 的最优化问题。
的最优化问题。
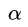 了!现在成了一个带约束的,变量只有
了!现在成了一个带约束的,变量只有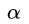 的最优化问题。
的最优化问题。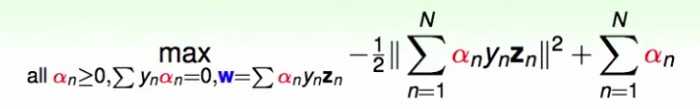
这个问题同时有等式约束和不等式约束,通过求解KKT条件,就可以得到最优解的候选解。也就是说,最优解必须满足KKT条件(必要条件)(当原问题是凸问题时,则是充分必要条件,刚好这个问题也是凸问题),也就是说,下面这些条件是dual SVM最优的b, w, 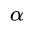 的充分必要条件:
的充分必要条件:
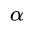 的充分必要条件:
的充分必要条件:
整理上面的最优化问题,将最大化换成最小化:

可以看到,有N个变量,N+1个限制条件(因为这个问题的变量只有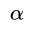 ,顾暂不考虑约束条件
,顾暂不考虑约束条件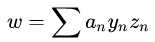 )
)
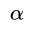 ,顾暂不考虑约束条件
,顾暂不考虑约束条件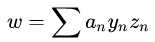 )
)这个问题也是一个二次规划问题,将其表示成标准的二次规划问题,就可以用二次规划算法求解了:

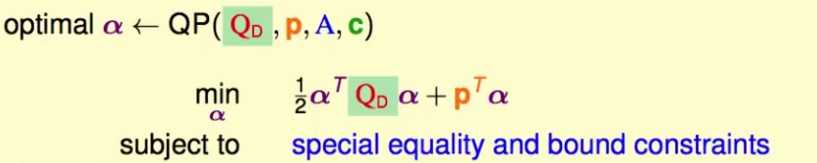
这里的Q_D矩阵是样本点的内积矩阵(N*d d*N -> N*N 核函数~),特别大,而且十分稠密,需要用特殊的为SVM准备的二次规划算法求解:

解出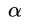 后,利用KKT条件求出w,b:
后,利用KKT条件求出w,b:
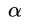 后,利用KKT条件求出w,b:
后,利用KKT条件求出w,b:w: 显然可以用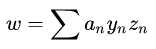 求解
求解
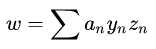 求解
求解b: 利用任何一个不是0的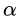 ,根据
,根据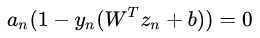 求解。同时,
求解。同时,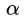 不等于0,代表这个点是支持向量。
不等于0,代表这个点是支持向量。
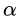 ,根据
,根据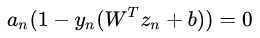 求解。同时,
求解。同时,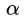 不等于0,代表这个点是支持向量。
不等于0,代表这个点是支持向量。
dual SVM的理解
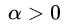 的那些点是支持向量(注意
的那些点是支持向量(注意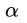 =0但是也在margin边界上的点不再是支持向量了,
=0但是也在margin边界上的点不再是支持向量了,即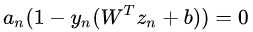 里的两项都=0
里的两项都=0
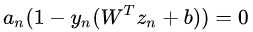 里的两项都=0
里的两项都=0)

回顾求解W的公式,发现W只与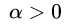 的那些
的那些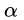 有关,同理,b也是:
有关,同理,b也是:
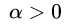 的那些
的那些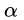 有关,同理,b也是:
有关,同理,b也是: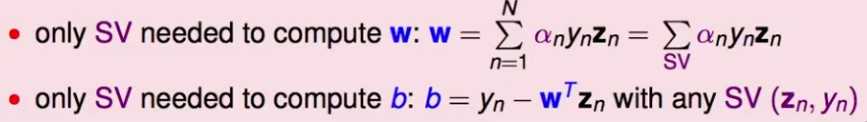
即,w和b都可以只依赖支持向量计算出来。(这也是为什么即使在边界上,但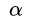 =0d的样本点不是支持向量,以为它们对求解w,b没有贡献)
=0d的样本点不是支持向量,以为它们对求解w,b没有贡献)
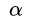 =0d的样本点不是支持向量,以为它们对求解w,b没有贡献)
=0d的样本点不是支持向量,以为它们对求解w,b没有贡献)对比SVM和感知机,这里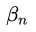 是训练时在样本n上犯错的次数:
是训练时在样本n上犯错的次数:
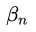 是训练时在样本n上犯错的次数:
是训练时在样本n上犯错的次数: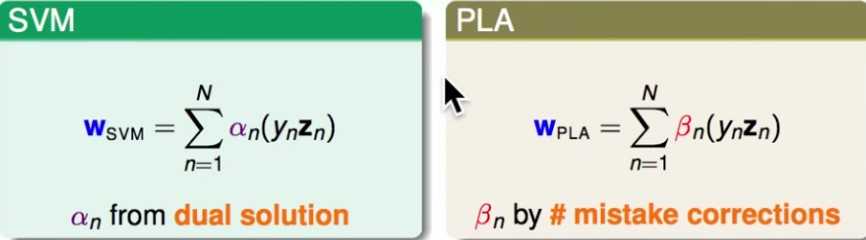
可以发现w都是原始资料的线性组合,即w可以被训练数据表示出来!
SVM认为重要的是支持向量,感知机认为重要的是犯错误的点,用它们来表示最后的w

对比原始SVM和dual SVM:
原始问题在特征维度较小时更为适合,dual SVM在样本数目较小时更为适合。

dual SVM真的和特征维度无关吗?其实隐藏在Q矩阵中:

这里有样本点的内积,与特征维度是相关的!如何让样本点的内积的成本与特征维度无关 —————— 核函数!
核函数
之间说对偶问题的优化目标中包含样本点的内积,这使得问题的求解依然与特征的维度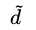 有关,因此如果将特征往高维空间转换,依然会带来较大的计算代价。
有关,因此如果将特征往高维空间转换,依然会带来较大的计算代价。
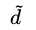 有关,因此如果将特征往高维空间转换,依然会带来较大的计算代价。
有关,因此如果将特征往高维空间转换,依然会带来较大的计算代价。而核函数就是一个解决样本内积的trick,让高维空间的样本特征的内积可以在低维空间完成。

推导核函数,以二维的多项式转化为例:
d维特征的样本在转化到二维上结果如下:

接下来计算两个样本点的内积,注意内积是两个样本点的对应特征相乘,而不是笛卡尔积两两相乘:
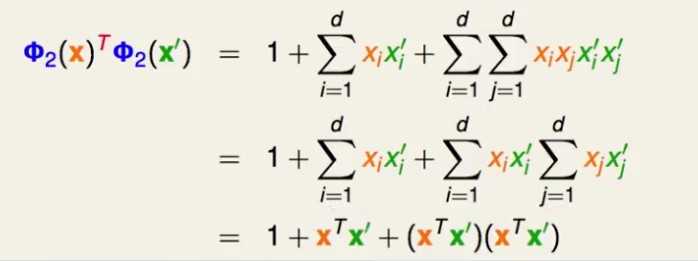
可以发现,不用先转换,再内积;而是可以先内积,再转换!
这样时间复杂度还是O(d):

这个过程就是kernel函数。刚才的转化的kernel函数就是:
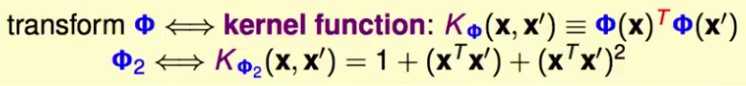
将kernel方法应用于Q矩阵的计算,以及参数b的计算,以及最终SVM模型在预测时的计算:

没有任何一个时刻真正的在z空间做内积,只需要在x空间做内积。
kernel SVM的二次规划算法

kernel SVM的时间复杂度:

多项式核函数
通过更改kernel函数里每一项的系数,就可以得到不同的从X空间到Z空间的转换:
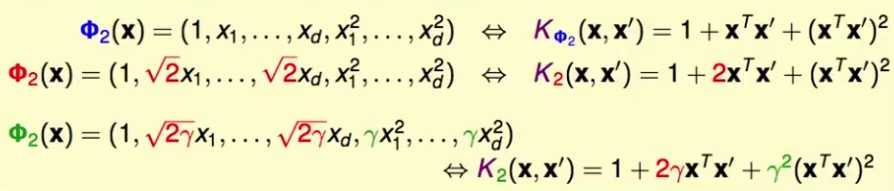

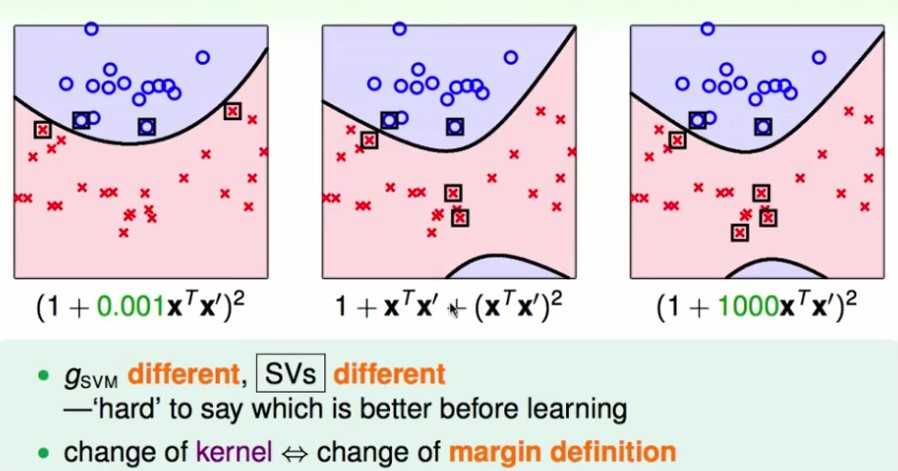
一般的多项式kernel
使用两个参数构造不同的kernel
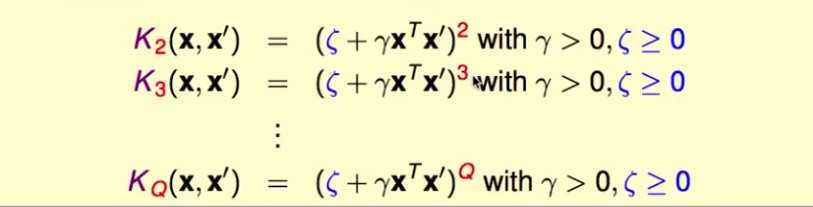
使用高维的kernel不用付出太大的计算代价,10次转换和2次转换代价基本一样:

同时由于SVM本身依靠较大的边界来降低模型的复杂度,因此使用高维的kernel也不用付出太大的模型复杂度的代价。
特例:1次kernel,没有什么变化;对于新问题,先尝试linear kernel。

高斯kernel —— 无限维
假设样本只有1个维度,证明 高斯核函数 等价于 无限维的转换:(证明中涉及到泰勒展开)
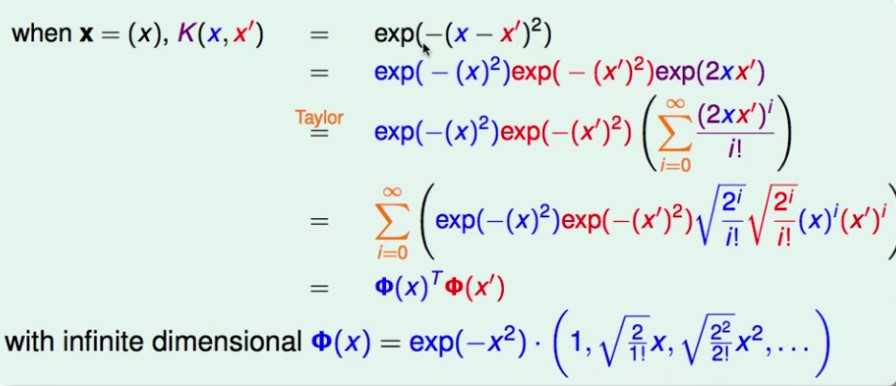
更一般的高斯kernel
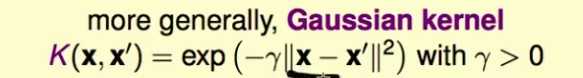
最后的SVM是中心在支持向量上的高斯函数的线性组合,也被称为RBF kernel。


高斯kernel里的参数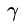 控制高斯函数的方差,当
控制高斯函数的方差,当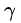 变大,高斯函数变陡,分类面也就越复杂。就算是SVM也会过拟合。
变大,高斯函数变陡,分类面也就越复杂。就算是SVM也会过拟合。
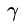 控制高斯函数的方差,当
控制高斯函数的方差,当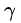 变大,高斯函数变陡,分类面也就越复杂。就算是SVM也会过拟合。
变大,高斯函数变陡,分类面也就越复杂。就算是SVM也会过拟合。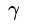 值需要谨慎选择
值需要谨慎选择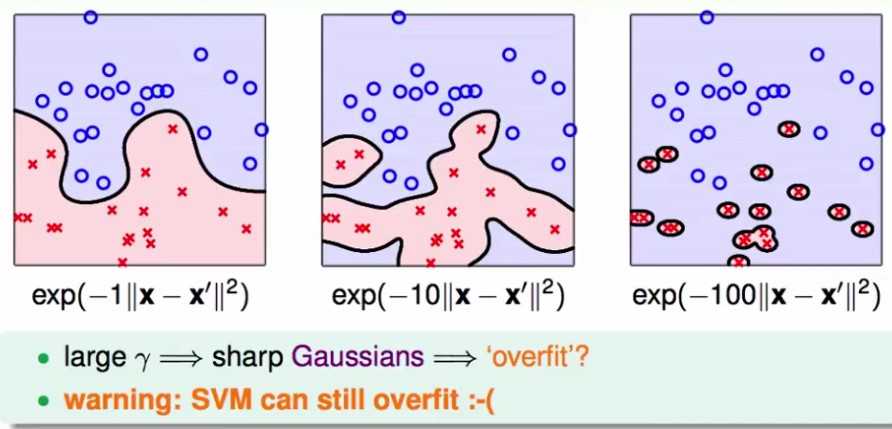
如果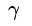 变成无穷大呢?
变成无穷大呢?
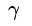 变成无穷大呢?
变成无穷大呢?

不同kernel的比较
linear kernel:
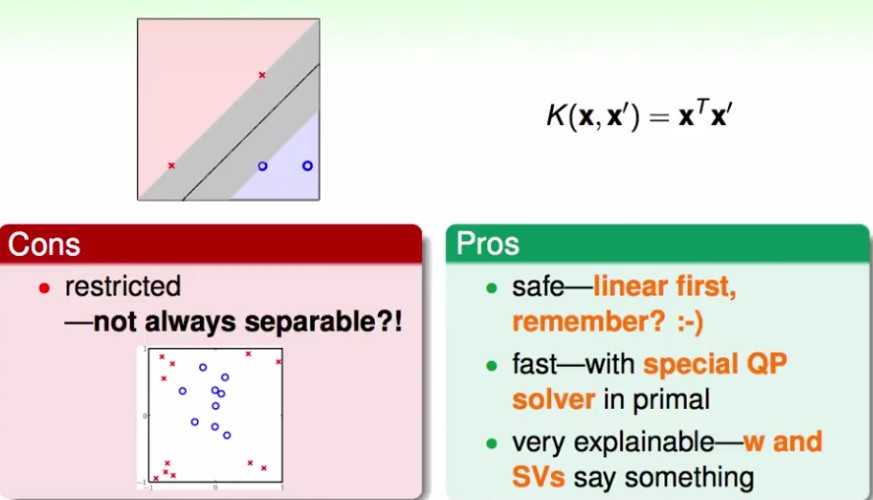
polynomial kernel:
缺点:
1) 随着转换的空间维度增高,会放大或缩小原来的样本的值,造成计算上的困难。
2) 需要设定更多的参数
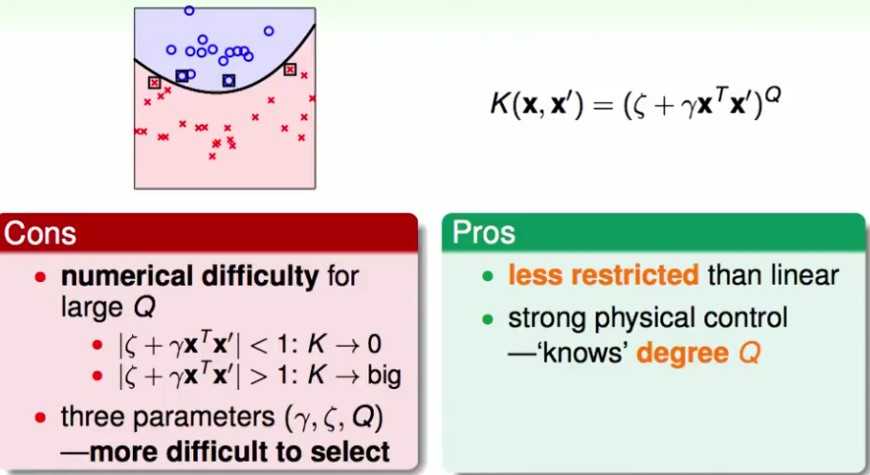
一般只用在幂次Q较小的情形,较大了也不会用polynomial kernel
Gaussian Kernel
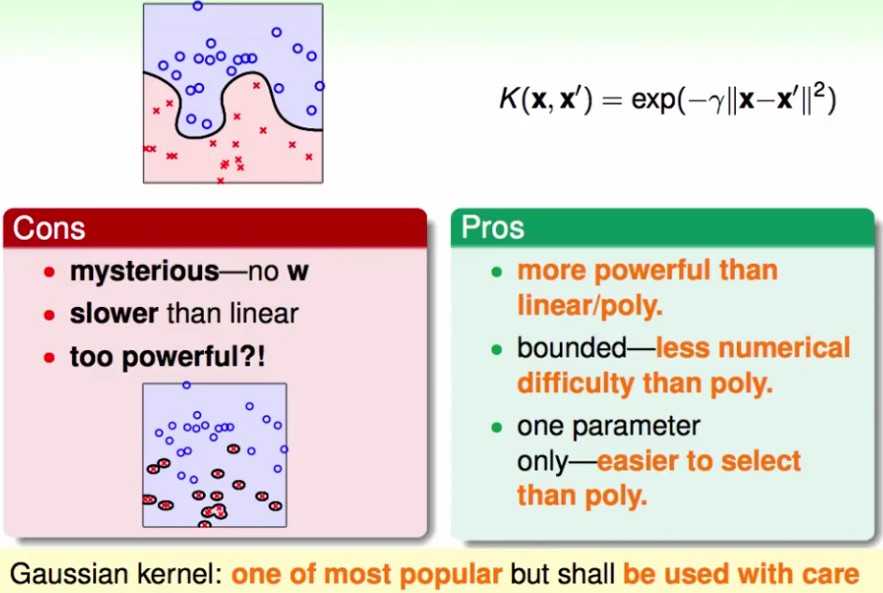
其他的kernel:
先要证明一个转换方式是一个kernel,为此,需要证明它满足kernel的一些性质: Mercer‘s condition
1) 对称性
2) 转换再内积 = 内积再转换

Soft-margin SVM
hard margin不管对什么资料,都要坚持能够分开,这意味着shatter,因此有过拟合的倾向。
hard-margin SVM过拟合:
1) 过于复杂的kernel转换
2) 坚持分开 —— hard margin

soft margin: 能够容忍一些错误
naive idea:在优化目标里加上错误的点的惩罚,同时放松错误的点的限制条件

整理上述问题:
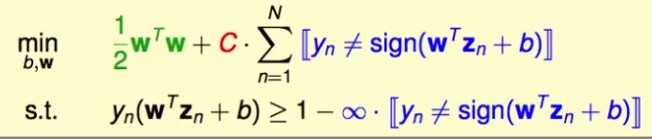
这已经不是一个二次规划问题了,因为限制条件了出现了非线性。另外一个缺点是不能区分小错误和大错误,离边界近的点和远的点都被视为犯错,一视同仁。
因此,改进这种思路,得到以下的问题:
为每个样本增加一个参数,表示它可以“过界”的距离,即它已经到边界里面的了,小于最小的margin了。这个参数放松了margin的限制,但同时在优化目标里也会惩罚“过界”的距离。

最小化时除了b,w,还多了一组参数: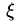
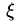
这依然是一个二次规划问题。

参数C的影响:

多处的N个变量是N个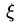 ,多出的N个限制条件是
,多出的N个限制条件是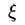 都要大于等于0,这样才是放宽边界的限制,允许跑到边界里面去。
都要大于等于0,这样才是放宽边界的限制,允许跑到边界里面去。
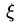 ,多出的N个限制条件是
,多出的N个限制条件是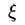 都要大于等于0,这样才是放宽边界的限制,允许跑到边界里面去。
都要大于等于0,这样才是放宽边界的限制,允许跑到边界里面去。dual Soft-margin SVM
推导dual soft-margin SVM的对偶问题
原问题
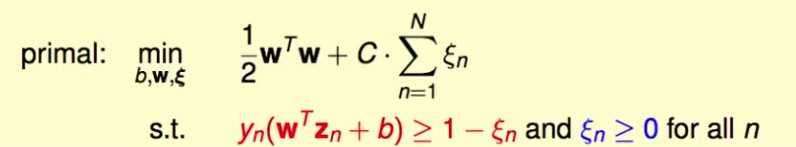
其拉格朗日函数是:
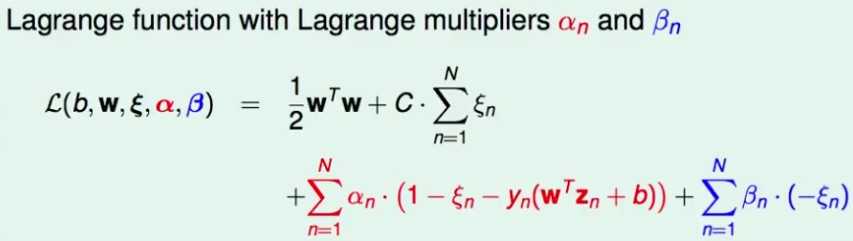
这里跳过证明最小最大问题在SVM里与最大最小问题最优解相同,直接求解对偶问题。
希望得到其对偶问题,即最大最小问题:

对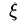 求偏导,可以消掉 beta,但是beta >=0 , 因而要求alpha <= C
求偏导,可以消掉 beta,但是beta >=0 , 因而要求alpha <= C
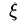 求偏导,可以消掉 beta,但是beta >=0 , 因而要求alpha <= C
求偏导,可以消掉 beta,但是beta >=0 , 因而要求alpha <= C
将等式带入原来的优化目标,可以进一步化简,消掉了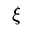
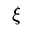
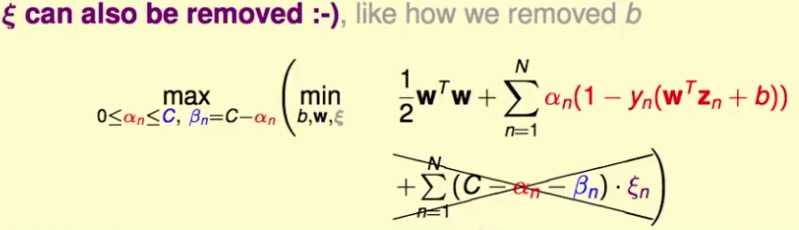
问题变成:
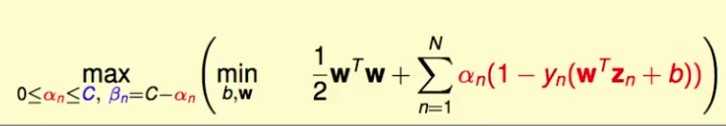
该问题和hard margin的优化目标一样,只是多了一点限制条件

问题变成:

和hard margin一模一样,只是多了一点限制条件
总结hard margin 和 soft margin

理解soft margin SVM
由于这个问题和hard margin SVM最终的优化问题有点不同,因此之前的KKT条件已经发生了改变。现在要如何求解b呢?
之前hard margin SVM是找一个alpha不等于0的样本点,利用该样本点在边界上的等式求出b。
根据hard margin的约束条件,其KKT条件中包含一个complementary slackness条件:
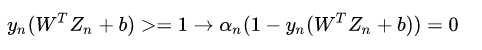 ,用该条件可以选择一个支持向量求出b
,用该条件可以选择一个支持向量求出b对于soft margin SVM, 根据其约束条件,其KKT条件有两个complementary slackness条件:
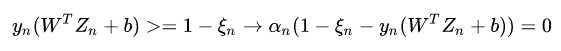
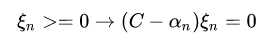 这里
这里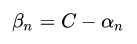
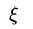 等于0意味着样本点没有违反边界,即样本点在边界上或者在边界外,而不在边界内
等于0意味着样本点没有违反边界,即样本点在边界上或者在边界外,而不在边界内
高斯核函数的soft margin SVM
可见C越大,对错误的容忍越小,越容易过拟合
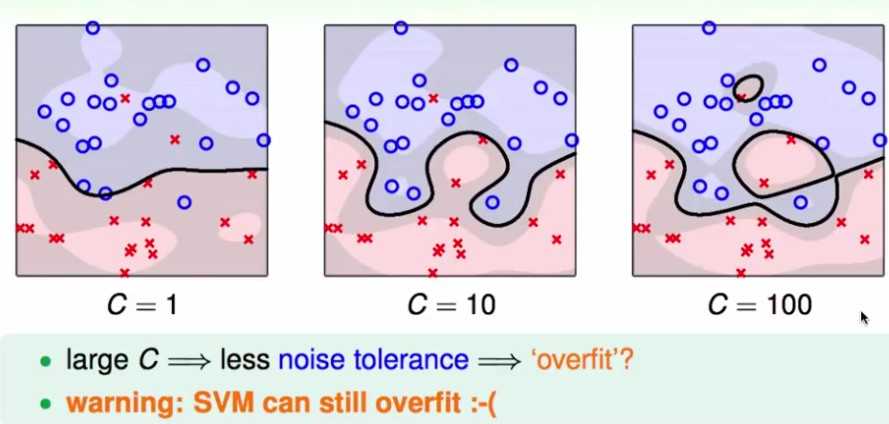
理解 soft margin SVM
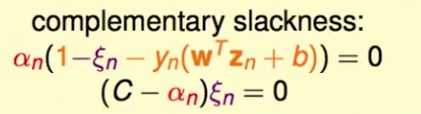
考虑这两个条件
如果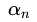 =0, 那么根据第二个等式,
=0, 那么根据第二个等式,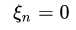 , 也就是说样本点没有违反边界,因此表示那些在边界上或者边界外的点
, 也就是说样本点没有违反边界,因此表示那些在边界上或者边界外的点
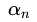 =0, 那么根据第二个等式,
=0, 那么根据第二个等式,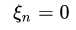 , 也就是说样本点没有违反边界,因此表示那些在边界上或者边界外的点
, 也就是说样本点没有违反边界,因此表示那些在边界上或者边界外的点如果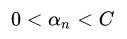 ,那么根据第一个等式和第二个等式,
,那么根据第一个等式和第二个等式,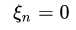 ,表明是在边界上的样本点
,表明是在边界上的样本点
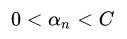 ,那么根据第一个等式和第二个等式,
,那么根据第一个等式和第二个等式,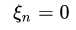 ,表明是在边界上的样本点
,表明是在边界上的样本点如果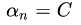 , 根据第二个等式,
, 根据第二个等式, ,表示样本点违反了边界,因而是那些在边界内部的点
,表示样本点违反了边界,因而是那些在边界内部的点
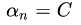 , 根据第二个等式,
, 根据第二个等式, ,表示样本点违反了边界,因而是那些在边界内部的点
,表示样本点违反了边界,因而是那些在边界内部的点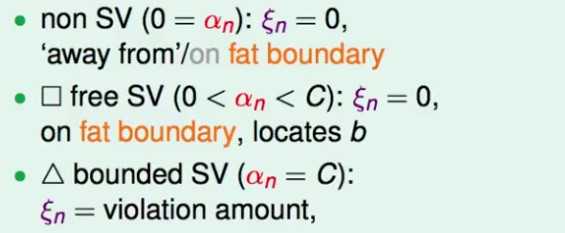
如果对SVM做leave-one-out CV,可以证明CV的误差与支持向量的比例有关

这其实印证了去掉不是支持向量的样本点,对模型没有影响。
hinge loss
考虑soft margin SVM, 换一个视角看它的优化目标,即将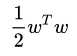 看成正则项,而将soft margin的松弛导致的误差项看做是损失函数。
看成正则项,而将soft margin的松弛导致的误差项看做是损失函数。
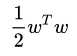 看成正则项,而将soft margin的松弛导致的误差项看做是损失函数。
看成正则项,而将soft margin的松弛导致的误差项看做是损失函数。首先,看一下松弛项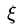 是怎么求的:
是怎么求的:
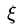 是怎么求的:
是怎么求的:
将这个目标函数看成是带正则项的损失函数最小化问题。这样,最后松弛项的误差看成是损失函数。为什么不直接解这个函数呢,1)不能用二次规划;2)不可微;
看一下这个“损失函数”的图像:(这是对正样本的图像,即如果不是>0,就是误分类)

这就是hinge loss的来源了
曲线是logistic regression的损失函数,即

可以发现,hinge loss和log loss非常像。因此,解SVM得到的W,b可以代入logistic regression作为近似解。
SVM 约等于 带L2正则项的Logistic Regression
如何使用SVM预测概率
将SVM的预测结果,作为单一维度的特征,再训练一个Logistic Regression,再做概率预测。