启发式搜索——A*算法

Posted 2020-10-26 bennettz

启发式搜索

启发式搜索是一种对搜索到的每一个位置进行评估，然后从评估的最优位置进行搜索直到目的地，
由于搜索时对每一个位置的评估是基于直观或经验的所有叫启发式搜索

A*算法

历史：

1964年Nils Nilsson提出了A1算法，是一个启发式搜索算法，
而后又被改进成为A2算法，直到1968年，被Peter E. Hart改进成为A*算法

主要思想：

1.对于每个搜索到的点求一个估价函数f(x)。
$\\large f(x)=g(x)+h(x)$
其中g(x)表示起点到当前点实际走的代价，h(x)表示当前点x到终点的估算代价。
2.并将这个搜索到的点按f(x)加入一个待搜索列表中。
3.每次从待搜索列表取出f(x)最小的点加入搜索过列表，并从这个点开始进行搜索
4.重复1。

注意：如果搜索到的一个点已经在待搜索列表(在搜索过列表不算)中
则要更新它的f值，而不是什么也不做，因为可能出现下面这种情况

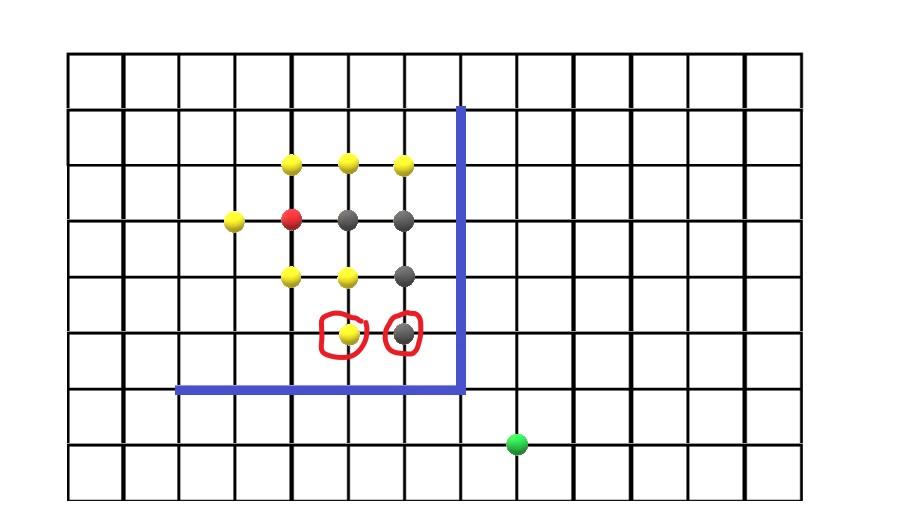
红色为起点，绿色为终点，灰色为搜索过列表中的点，黄色为待搜索列表中的点，蓝色的是障碍。
如果按和终点的曼哈顿距离算h(x)则会搜索成这种情况，
这时被圈出的黄色的点g(x)=被圈出的灰色的点的g(x)+1。

这显然不是最优的g值
所以搜索时在遇到待搜索列表中的点要更新它的f值

h函数的选择

由于h函数只是一个估计值，所以对于每个题目可以有许多h函数的选择方法

选择不同的h函数会有不同的效果，但大致有两条规律：

1. 如果h(x)>x到终点的实际代价，则可以尽快找到一个解，但不一定是最优解
2. 如果$h(x)\\le$x到终点的实际代价，则如果有解，一定是最优解
   且h(x)和x到终点的实际代价相差越大，搜到的无关节点越多

例题

luoguP1379 八数码难题

#include<cstdio>
#include<cmath>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
const int fac[]={1, 1, 2, 6, 24, 120, 720, 5040, 40320};
int cantor(int a[],int k){//康托展开 
    int ans=0,tmp;
    for(int i=0;i<k;i++){
        tmp=0;
        for(int j=i+1;j<k;j++){
            if(a[i]>a[j])tmp++;
        }
        ans+=tmp*fac[k-i-1];
    }
    return ans;
}
void uncantor(int a[],int k,int num){//逆康托展开 
    int b[10];
    for(int i=0;i<k;i++)b[i]=i+1;
    b[k]=0;
    for(int i=0,x;i<k;i++){
        x=num/fac[k-i-1],num%=fac[k-1-i];
        a[i]=b[x]-1;
        for(int j=x;b[j];j++)b[j]=b[j+1];
    }
} 
int ma,dis[10][10],go[4][2]={{1,0},{-1,0},{0,1},{0,-1}},a[10],b[10];
bool vis[370000];
int h(){//估价代价 
    int ans=0;
    for(int i=0,j;i<9;i++){
        for(j=0;j<9;j++){
            if(a[i]==b[j])break;
        }
        if(a[i])ans+=dis[i][j];
    }
    return ans;
}
struct Node{
    int x,f,g;//x为状态的康托展开值, 
    bool operator < (const Node &b)const{
        return f>b.f;
    }
}node,w;
priority_queue<Node> q;
int astr(int now,int t){//A*算法 
    node.x=now;
    node.f=h();
    node.g=0;
    q.push(node);
    while(!q.empty()){
        w=q.top(),q.pop();
        if(vis[w.x])continue;
        vis[w.x]=1;
        if(w.x==t){
            return w.f;
        }
        uncantor(a,9,w.x);
        int x,y;
        for(int i=0;i<9;i++){
            if(a[i]==0){
                x=i/3,y=i%3;break;
            }
        }
        for(int i=0;i<4;i++){
            int x1=x+go[i][0],y1=y+go[i][1];
            if(x1>=0&&x1<3&&y1>=0&&y1<3){
                swap(a[x1*3+y1],a[x*3+y]);
                node.x=cantor(a,9),node.g=w.g+1,node.f=h()+node.g;
                if(!vis[node.x])q.push(node);
                swap(a[x1*3+y1],a[x*3+y]);
            }
        }
    }
    return 0;
}
int main(){
    char s[10];int st,t;
    sscanf("123804765","%s",s);
    for(int i=0;i<9;i++)b[i]=s[i]^0x30;
    t=cantor(b,9);
    scanf("%s",s);
    for(int i=0;i<9;i++)a[i]=s[i]^0x30;
    st=cantor(a,9);
    vis[st]=1;
    for(int i=0;i<9;i++){
        for(int j=i+1;j<9;j++){
            dis[j][i]=dis[i][j]=j/3-i/3+abs(i%3-j%3);
        }
    }
    memset(vis,0,sizeof(vis));
    printf("%d",astr(st,t));
    return 0;
} 

IDA*

A*算法和bfs一样都要记录每个节点是否被访问过了，有些题目的状态不好表示

使用A*算法就会非常麻烦，这时就可以使用IDDFS的A*思想优化版IDA*(IDA*并不是迭代加深A*)

具体操作

具体操作和IDDFS基本一样：

1. 确定一个限制深度，然后进行DFS
2. 如果在限制深度内得不到解就将限制深度加深，继续DFS
3. 如果得到解就输出

只是在dfs的时候利用A*思想估计剩余深度，如果当前深度+估计值>限制深度就退出本次搜索

例题 hdu1667 The Rotation Game

/******************************************************************
IDA*
******************************************************************/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int center[] = {6,7,8,11,12,15,16,17};  //中心8个点的位置 
const int reversetp[] = {5,4,7,6,1,0,3,2};  //每种操作的逆操作
const int op[8][7] = {  //从A-H操作的值的下标
    { 0 ,2 ,6 ,11,15,20,22 },    //A
    { 1 ,3 ,8 ,12,17,21,23 },    //B
    { 10,9 ,8 ,7 ,6 ,5 ,4  },    //C
    { 19,18,17,16,15,14,13 },    //D
    { 23,21,17,12,8 ,3 ,1  },    //E
    { 22,20,15,11,6 ,2 ,0  },    //F 
    { 13,14,15,16,17,18,19 },    //G
    { 4 ,5 ,6 ,7 ,8 ,9 ,10 },    //H
};
int a[24];
int h(){
    int num[3]={0};
    for(int i=0;i<8;i++){
        num[a[center[i]]-1]++;
    }
    return 8-max(num[0],max(num[1],num[2]));
}
bool f;char ans[105];
void modify(int x){
    int w=a[op[x][0]];
    for(int i=0;i<6;i++)a[op[x][i]]=a[op[x][i+1]];
    a[op[x][6]]=w;
}
void idastar(int d,int maxd){
    if(f)return;
    if(d==maxd){
        if(!h())f=1,ans[d]=0,printf("%s\\n%d\\n",ans,a[6]);
        return;
    }
    if(d>maxd||d+h()>maxd)return;
    for(int i=0;i<8;i++){
        modify(i);
        ans[d]=(i^0x40)+1,idastar(d+1,maxd);
        modify(reversetp[i]);
    }
}
void work(){
    for(int i=1;i<24;i++)scanf("%d",a+i);
    if(!h()){
        printf("No moves needed\\n%d\\n",a[6]);
        return;
    }
    f=0;
    for(int i=1;;i++){
        idastar(0,i);
        if(f)return;
    }
}
int main(){
    while(~scanf("%d",a)&&a[0])work();
    return 0;
}