一.作业题目
仿照三元组或复数的抽象数据类型写出有理数抽象数据类型的描述 (有理数是其分子、分母均为整数且分母不为零的分数)。
有理数基本运算:
- 构造有理数T,元素e1,e2分别被赋以分子、分母值
- 销毁有理数T
- 用e(引用类型参数)返回有理数T的分子或分母,当入参i为1时返回分子, i为2是返回分母。
- 将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母
- 有理数T1,T2相加,结果存入有理数T3
- 有理数T1,T2相减,结果存入有理数T3
- 有理数T1,T2相乘,结果存入有理数T3
- 有理数T1,T2相除,结果存入有理数T3
实验要求: - 抽象数据类型名为Rational。
- 有理数分母不能为负数或者0,类似输入请提示重输入。
- 数据对象和数据运算的表示与数据操作的实现分离。表示用头文件完成,实现用CPP文件完成。Main.cpp文件实现数据输入输出。
- 数据输入输出格式参考如下:
输入:
1 3 //T1的分子、分母
1 2 //T2的分子、分母
** 输出:**
5 6 //两个有理数相加
-1 6 //两个有理数相减
1 6 //两个有理数相乘
2 3 //两个有理数相除
程序应对异常输入或者出错必要处理和提示,比如提示:“分数是否需要约分等”。
二.作业内容
1、用ADT的抽象数据模型描述你的有理数数据类型
ADT Rational-Num{
数据对象:D = {T1,T2,T3|T1,T2,T3为有理数}
数据关系:R = {<T1,T2>,<T2,T3>}
基本操作:
InitTriplet(Triplet &T, ElemType v1, ElemType v2)
操作结果:构造一个有理数T,其分子和分母分别为e1和e2
DestroyTriplet(Triplet &T)
操作结果:销毁有理数T
Get(Triplet T, int i, ElemType &e)
操作结果:用e返回有理数T的分子或分母,i为1时返回分子, i为2是返回分母
Put(Triplet &T, int i, ElemType e)
操作结果:将有理数T的分子或分母更改为e,i为1时改变分子, i为2是改变分母
Add(Triplet &T1,Triplet &T2,Triplet &T3)
操作结果:将T1,T2相加,结果存入T3
Sub(Triplet &T1,Triplet &T2,Triplet &T3)
操作结果:将T1,T2相减,结果存入T3
Mul(Triplet &T1,Triplet &T2,Triplet &T3)
操作结果:将T1,T2相乘,结果存入T3
Div(Triplet &T1,Trplet &T2,Triplet &T3)
操作结果:将T1,T2相除,结果存入T3
} ADT Rational-Num
2.数据结构,函数说明

3.代码实现说明
相加

相减
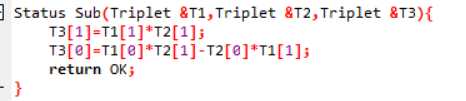
相乘

相除
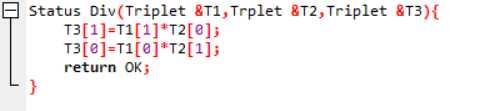
计算公约数方法:辗转相除法

运行结果
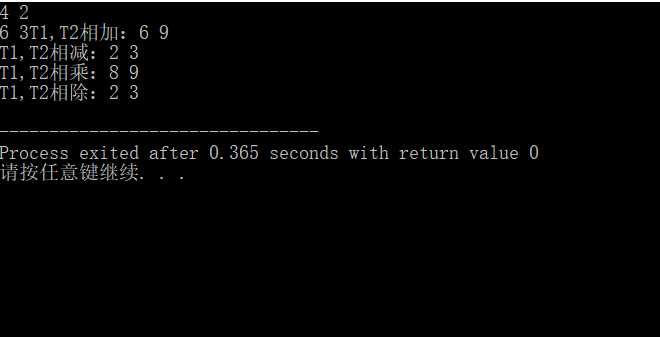

总结:学会了数据结构的运用,辗转相除法的运用