题目描述
H国是一个热爱写代码的国家,那里的人们很小去学校学习写各种各样的数据结构。伸展树(splay)是一种数据结构,因为代码好写,功能多,效率高,掌握这种数据结构成为了H国的必修技能。有一天,邪恶的“卡”带着他的邪恶的“常数”来企图毁灭H国。“卡”给H国的人洗脑说,splay如果写成单旋的,将会更快。“卡”称“单旋splay”为“spaly”。虽说他说的很没道理,但还是有H国的人相信了,小H就是其中之一,spaly马上成为他的信仰。而H国的国王,自然不允许这样的风气蔓延,国王构造了一组数据,数据由m(不超过10^5)个操作构成,他知道这样的数据肯定打垮spaly,但是国王还有很多很多其他的事情要做,所以统计每个操作
所需要的实际代价的任务就交给你啦。数据中的操作分为5种:
-
插入操作:向当前非空spaly中插入一个关键码为key的新孤立节点。插入方法为,先让key和根比较,如果key比根小,则往左子树走,否则往右子树走,如此反复,直到某个时刻,key比当前子树根x小,而x的左子树为空,那就让key成为x的左孩子;或者key比当前子树根x大,而x的右子树为空,那就让key成为x的右孩子。该操作的代价为:插入后,key的深度。特别地,若树为空,则直接让新节点成为一个单个节点的树。(各节点关键码互不相等。对于“深度”的解释见末尾对spaly的描述。)
-
单旋最小值:将spaly中关键码最小的元素xmin单旋到根。操作代价为:单旋前xmin的深度。(对于单旋操作的解释见末尾对spaly的描述。)
-
单旋最大值:将spaly中关键码最大的元素xmax单旋到根。操作代价为:单旋前xmax的深度。
-
单旋删除最小值:先执行2号操作,然后把根删除。由于2号操作之后,根没有左子树,所以直接切断根和右子树的联系即可。(具体见样例解释)。操作代价同2号操作。
-
单旋删除最大值:先执行3号操作,然后把根删除。操作代价同3号操作。
对于不是H国的人,你可能需要了解一些spaly的知识,才能完成国王的任务:
-
spaly是一棵二叉树,满足对于任意一个节点x,它如果有左孩子lx,那么lx的关键码小于x的关键码。如果有右孩子rx,那么rx的关键码大于x的关键码。
-
一个节点在spaly的深度定义为:从根节点到该节点的路径上一共有多少个节点(包括自己)。
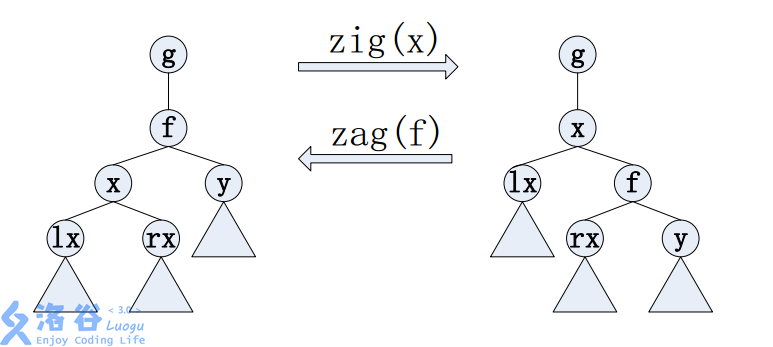
- 单旋操作是对于一棵树上的节点x来说的。一开始,设f为x在树上的父亲。如果x为f的左孩子,那么执行zig(x)操作(如上图中,左边的树经过zig(x)变为了右边的树),否则执行zag(x)操作(在上图中,将右边的树经过zag(f)就变成了左边的树)。每当执行一次zig(x)或者zag(x),x的深度减小1,如此反复,直到x为根。总之,单旋x就是通过反复执行zig和zag将x变为根。
输入输出格式
输入格式:输入文件名为 splay.in。
第一行单独一个正整数 m (1 <= m <= 10^5)。
接下来 m 行,每行描述一个操作:首先是一个操作编号 c( 1<=c<=5),既问题描述中给出的 5 种操作中的编号,若 c= 1,则再输入一个非负整数 key,表示新插入节点的关键码。
输出格式:输出文件名为 splay.out。
输出共 m 行,每行一个整数,第 i 行对应第 i 个输入的操作的代价。
输入输出样例
说明
20%的数据满足: 1 <= m <= 1000。
另外 30%的数据满足: 不存在 4,5 操作。
100%的数据满足: 1<=m<=10^5; 1<=key<=10^9。 所有出现的关键码互不相同。 任何一个非插入操作,一定保证树非空。 在未执行任何操作之前,树为空。
solution:首先hash插入值,用线段树保存hash值在树上的深度。由于我们只需要单旋最大值和最小值,通过手玩数据我们发现单旋最小值并不会改变树的形状,发生变化的只有最小值成为了根,最小值原来的右子树成为了他父亲的左子树,相应的最小值的深度不变,其它结点深度均+1,单旋最大值同理。对于插入值,我们只需找到他的前驱后继,再维护深度和父子关系即可,对于删除最大值和最小值,我们先将他们旋转到根,然后删除即可,找前驱后继可以维护一个动态的set,注意线段树的松弛操作。
#include<bits/stdc++.h> #define N 200010 using namespace std; int m,tp,root; int opt[N],v[N],q[N],ch[N][2],fa[N],dep[N*2]; set<int>st; int read() { int x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f*=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } void down(int rt) { if(dep[rt]) { dep[rt<<1]+=dep[rt]; dep[rt<<1|1]+=dep[rt]; dep[rt]=0; } } void modify(int rt,int l,int r,int pos,int val) { if(l==r){dep[rt]=val;return ;} down(rt); int mid=(l+r)>>1; if(pos<=mid)modify(rt<<1,l,mid,pos,val); else modify(rt<<1|1,mid+1,r,pos,val); } int query(int rt,int l,int r,int pos) { if(l==r)return dep[rt]; down(rt); int mid=(l+r)>>1; if(pos<=mid)return query(rt<<1,l,mid,pos); else return query(rt<<1|1,mid+1,r,pos); } void update(int rt,int l,int r,int L,int R,int k) { if(L<=l&&R>=r){dep[rt]+=k;return ;} down(rt); int mid=(l+r)>>1; if(L<=mid)update(rt<<1,l,mid,L,R,k); if(R>mid)update(rt<<1|1,mid+1,r,L,R,k); } int insert(int x) { set<int>::iterator it=st.insert(x).first;//定义前向迭代器,下标从插入元素开始 if(!root){root=x;modify(1,1,tp,x,1);return 1;}//空树,插入结点深度为1 if(it!=st.begin())//如果插入元素有前驱 { if(!ch[*--it][1])ch[fa[x]=*it][1]=x;//如果前驱没有右儿子 it++; } if(!fa[x])ch[fa[x]=*++it][0]=x;//要么成为后继的左儿子 int deep=query(1,1,tp,fa[x])+1; modify(1,1,tp,x,deep); return deep; } int findmax() { int x=*st.rbegin(),res=query(1,1,tp,x); if(x==root)return 1; if(x-1>=fa[x]+1)update(1,1,tp,fa[x]+1,x-1,-1);//x右树的深度都不变,所以先减1 update(1,1,tp,1,tp,1); ch[fa[x]][1]=ch[x][0]; fa[ch[x][0]]=fa[x]; ch[fa[root]=x][0]=root; root=x; modify(1,1,tp,x,1); return res; } int findmin() { int x=*st.begin(),res=query(1,1,tp,x);//找到最小值并询问深度 if(x==root)return 1; if(x+1<=fa[x]-1)//x有右子数 update(1,1,tp,x+1,fa[x]-1,-1);//x右树的深度都不变,所以先减1 update(1,1,tp,1,tp,1); ch[fa[x]][0]=ch[x][1]; fa[ch[x][1]]=fa[x]; ch[fa[root]=x][1]=root; root=x; modify(1,1,tp,x,1); return res; } void delmax() { printf("%d\n",findmax()); update(1,1,tp,1,tp,-1); st.erase(root); root=ch[root][0]; fa[root]=0; } void delmin() { printf("%d\n",findmin()); update(1,1,tp,1,tp,-1); st.erase(root); root=ch[root][1]; fa[root]=0; } int main() { m=read(); for(int i=1;i<=m;i++) { opt[i]=read(); if(opt[i]==1)q[++tp]=v[i]=read(); } sort(q+1,q+1+tp); for(int i=1;i<=m;i++) if(opt[i]==1)v[i]=lower_bound(q+1,q+1+tp,v[i])-q;//将插入的值离散化 for(int i=1;i<=m;i++) { if(opt[i]==1){printf("%d\n",insert(v[i]));} else if(opt[i]==2)printf("%d\n",findmin()); else if(opt[i]==3)printf("%d\n",findmax()); else if(opt[i]==4)delmin(); else if(opt[i]==5)delmax(); } return 0; }