图 Graph-图的相关算法
Posted hyserendipity
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了图 Graph-图的相关算法相关的知识,希望对你有一定的参考价值。
2018-03-06 17:42:02
一、最短路问题
问题描述:在网络中,求两个不同顶点之间的所有路径中,边的权值之和最小的那一条路径。
- 这条路径就是两点之间的最短路径 (Shortest Path)
- 第一个顶点为源点 (Source)
- 最后一个顶点为终点 (Destination)
问题分类:
- 单源最短路径问题:从某固定源点出发,求其到所有其他顶点的最短路径。
- (有向)无权图
- (有向)有权图
- 多源最短路径问题:求任意两顶点间的最短路径。
1)无权图的单源最短路算法
BFS可以解决这类问题。
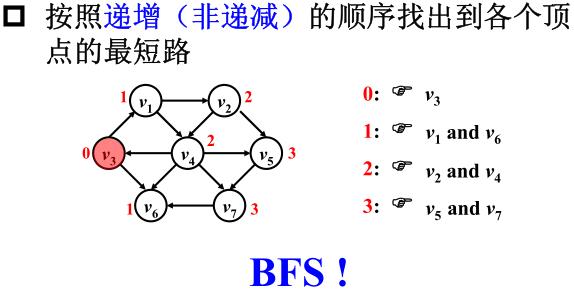

2)有权图的单源最短路算法
Dijkstra算法可以解决不带负值边的单源最短路问题。
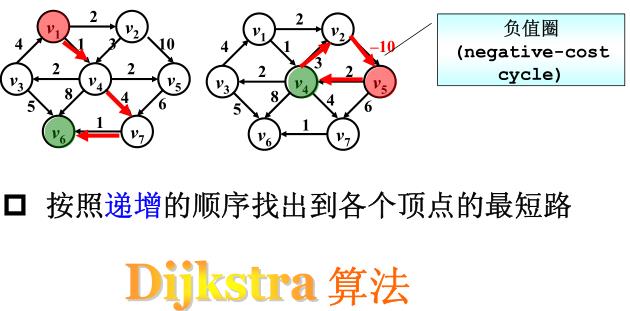


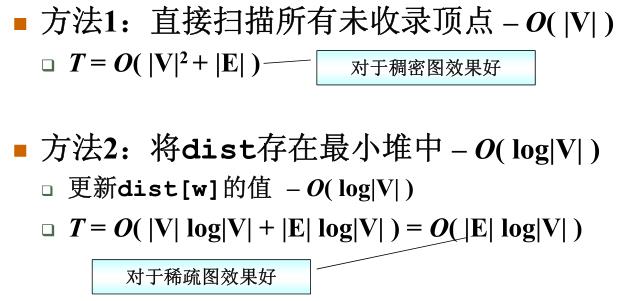
3)多源最短路算法
此算法由Robert W. Floyd(罗伯特·弗洛伊德)于1962年发表在“Communications of the ACM”上。同年Stephen Warshall(史蒂芬·沃舍尔)也独立发表了这个算法。Floyd这个牛人是朵奇葩,他原本在芝加哥大学读的文学,但是因为当时美国经济不太景气,找工作比较困难,无奈之下到西屋电气公司当了一名计算机操作员,在IBM650机房值夜班,并由此开始了他的计算机生涯。
我们来想一想,根据我们以往的经验,如果要让任意两点(例如从顶点a点到顶点b)之间的路程变短,只能引入第三个点(顶点k),并通过这个顶点k中转即a->k->b,才可能缩短原来从顶点a点到顶点b的路程。那么这个中转的顶点k是1~n中的哪个点呢?甚至有时候不只通过一个点,而是经过两个点或者更多点中转会更短,即a->k1->k2b->或者a->k1->k2…->k->i…->b。比如上图中从4号城市到3号城市(4->3)的路程e[4][3]原本是12。如果只通过1号城市中转(4->1->3),路程将缩短为11(e[4][1]+e[1][3]=5+6=11)。其实1号城市到3号城市也可以通过2号城市中转,使得1号到3号城市的路程缩短为5(e[1][2]+e[2][3]=2+3=5)。所以如果同时经过1号和2号两个城市中转的话,从4号城市到3号城市的路程会进一步缩短为10。通过这个的例子,我们发现每个顶点都有可能使得另外两个顶点之间的路程变短。
Floyd算法就是首先只允许经过0号结点,看看是否会变短,如果变短就加之修改,然后只允许经过0,1号结点,看看是否变短,加之修改,直到中间结点到达为所有可能的结点。


二、最小生成树 (Minimum Spanning Tree)
什么是最小生成树?
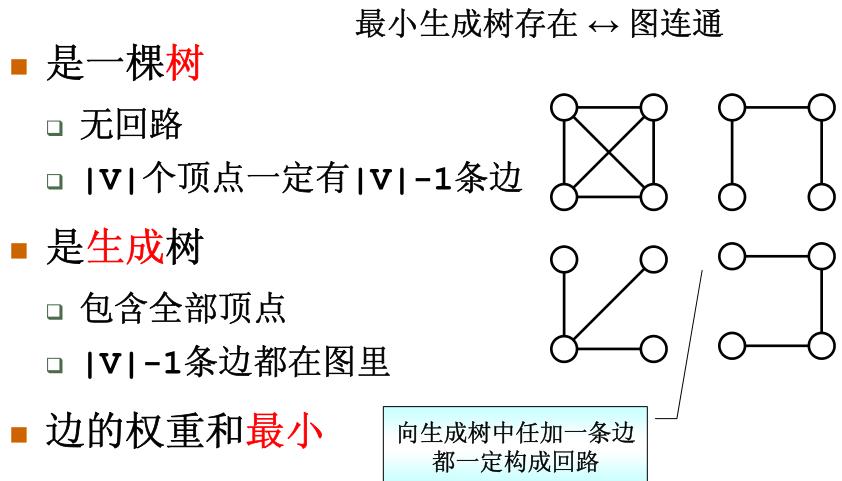
最小生成树算法使用贪心的思想,每一步都选权重最小的边。

- Prim算法 — 让一棵小树长大
首先随机选择起始点,然后不断将当前结点往外生长,寻找最短的结点加入。

- Kruskal算法 — 将森林合并成树

三、拓扑排序
拓扑序:如果图中从V到W有一条有向路径,则V一定排在W之前。满足此条件的顶点序列称为一个拓扑序。
获得一个拓扑序的过程就是拓扑排序。
AOV(Activity On Vertex)如果有合理的拓扑序,则必定是有向无环图(Directed Acyclic Graph, DAG)。

举个例子,将计算机学院的课程按照拓扑序进行输出。

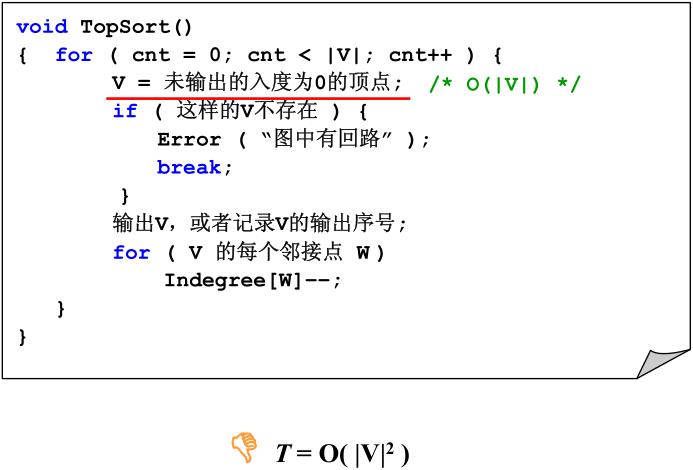
一种聪明的算法就是将入度为0的结点放到队列。

关键路径问题:
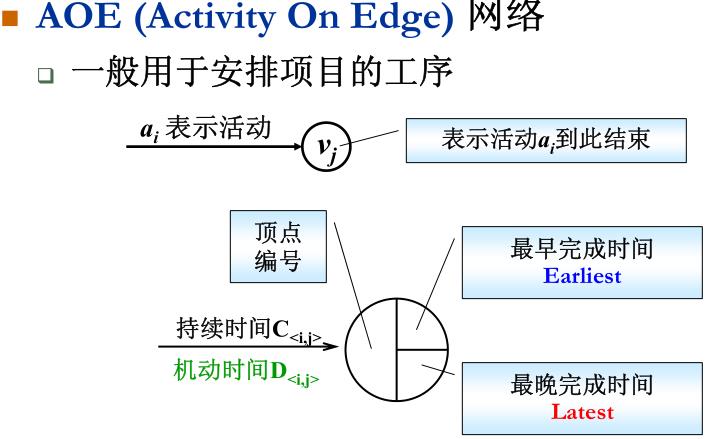
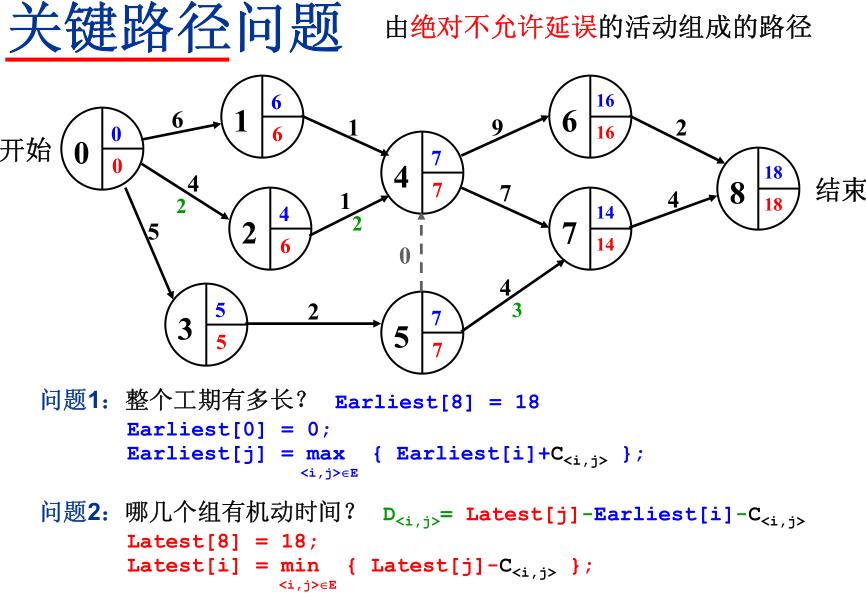
以上是关于图 Graph-图的相关算法的主要内容,如果未能解决你的问题,请参考以下文章