二叉树遍历有先序、中序和后序三种遍历方式。
先序:根左右
中序:左根右
后序:左右根
给出树的根节点后可根据递归求得不同的序列,这方面不是这的重点先按下不表。
这里的重点在于如何在知道了二叉树的2种遍历序列的基础上求得第3种遍历序列。这里有两种方法,一种是采用线段数的做法,第二种是采用建树的做法。
先来讲讲线段树的方法:
线段树就是采用数组来存储一棵树的节点编号,父子节点的数学关系如下
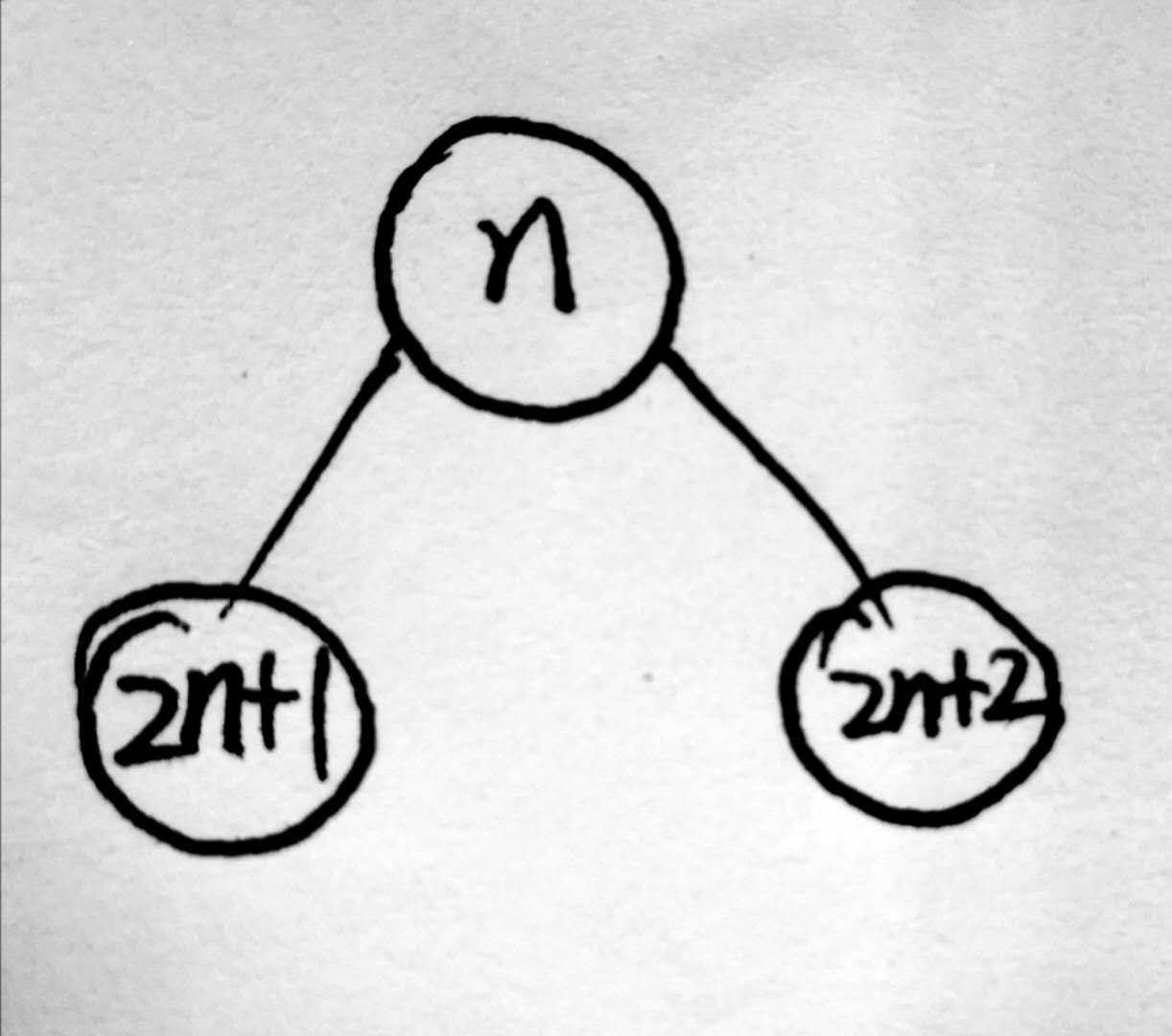
因此在线段树中我们得到一个节点编号后很容易就能确定它在树中位置以及他的父节点和子节点编号。
接下来,以“已知后序和中序序列求先序序列”为例讲讲如何知二求一!
下面我们给出一个后序遍历序列和一个中序遍历序列:
后序:2 3 1 5 7 6 4
中序:1 2 3 4 5 6 7
由二叉树遍历的性质我们知道后序遍历最后一个输出的根节点④,而根据中序遍历的性质我们也能知道根节点的两侧分别为左子树①②③和右子树⑤⑥⑦,后序遍历先看根节点的左子树那么我们根据其遍历的性质又可知道左子树的根节点①,再看中序序列发现①没有左子树只有右子树,因此根据后序序列它的右子树根为③且它只有左子树②。之后我们再来看④的右子树,根据后序遍历的性质有其右子树的根⑥,根据中序遍历知道了⑥的左右子树分别为⑤⑦。过程如下图:
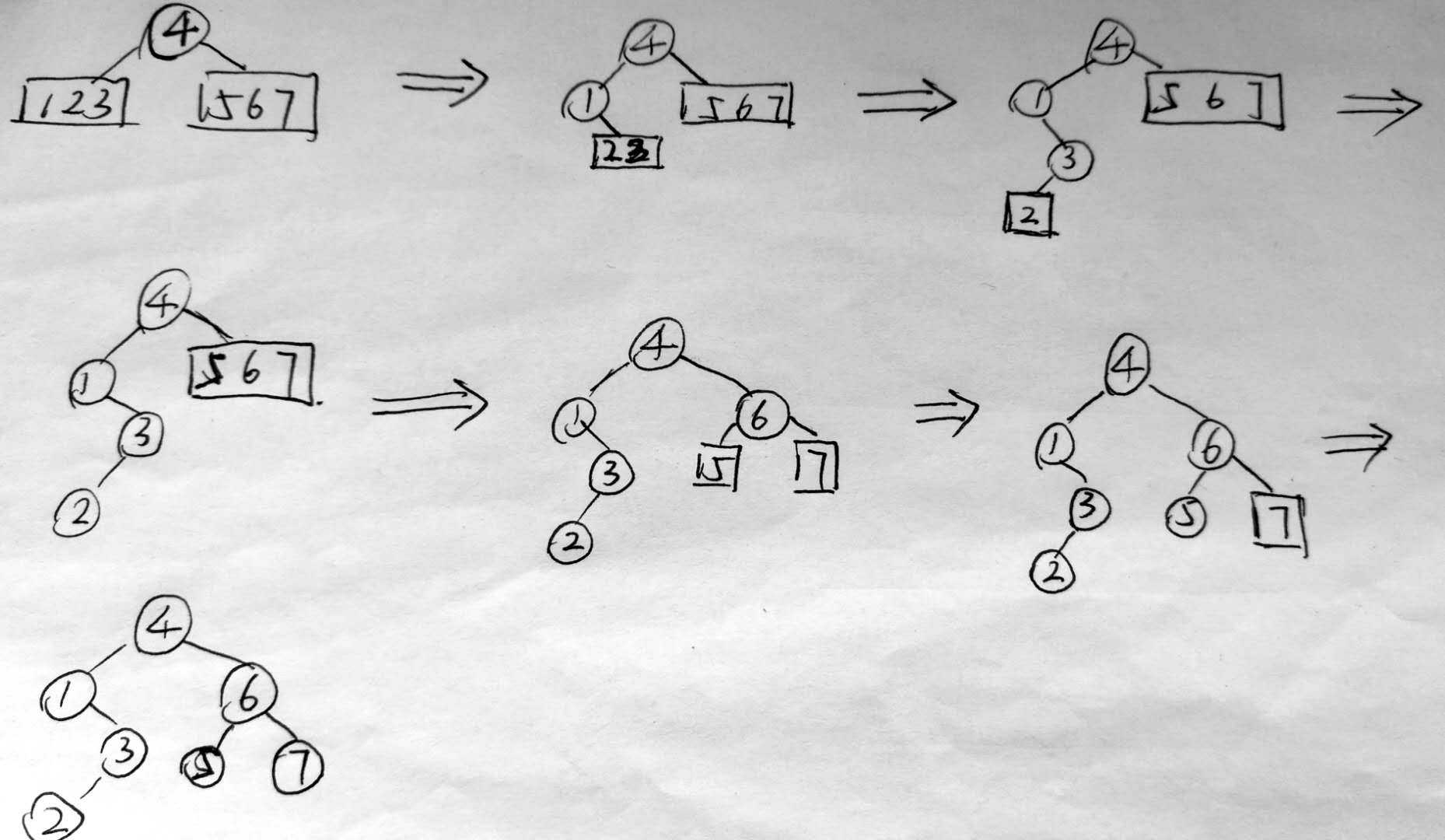
下面说下代码的实现(不建树的方法):
算法个关键就在于根据后序序列求出根节点然后在中序序列中找出根节点随之划分出左右子树,层层递归。1 //已知二叉树中序、后序,求先序。 2 #include<cstdio> 3 using namespace std; 4 5 int mid[7] = {1,2,3,4,5,6,7}; 6 int post[7] = {2,3,1,5,7,6,4}; 7 8 //root为根在后序遍历序列里的位置,start和end是子树的其实位置在中序遍历序列里的位置 9 void pre_order(int root,int start,int end){ 10 if(start>end) { 11 return; 12 } 13 int i; 14 i = start; 15 //中序序列中寻找根节点 16 while(i<end && mid[i] != post[root]) { 17 i++; 18 } 19 printf("%d ",post[root]) ; 20 //左子树根的位置(后序序列):当前根节点-右子树节点数-1 21 pre_order(root-(end-i)-1,start,i-1); 22 //右子树根的位置(后序序列):当前根节点-1 23 pre_order(root-1,i+1,end); 24 } 25 26 int main(){ 27 pre_order(6,0,6); 28 }
我们再来讲一下通过用建树的方法来求二叉树,这种方法比较复杂一般用于节点数太多的情况,二叉树是以链表的形式存储的。
我们一般先用写一个节点类型的结构体
struct Tree{ int r; Tree *leftCid,*rightCid; };
之后是递归函数建树的过程:
Tree* order(int root,int begin,int end){ if(begin>end) { return NULL; } int i; i = begin; Tree *pn; pn = new Tree(); while(i<end && mid[i] != pri[root]){ i++; } pn->r = pri[root]; pn->leftCid = order(root+1,begin,i-1); pn->rightCid = order(root+(i-begin)+1,i+1,end); return pn; }
int main(){ int n; Tree *node = NULL; scanf("%d",&n); for(int i=0;i<n;i++){ scanf("%d",&mid[i]); } for(int i=0;i<n;i++){ scanf("%d",&pri[i]); } node = order(0,0,n-1); }
注意这里函数返回的是指针,因为结构体中左右孩子都是指针类型,为了统一类型初始设根节点最好也要为指针类型。
还有就是在C++里动态开辟内存要写为:
Tree *pn; pn = new Tree();
意思就是,先创建一个指针类型的变量,再向内存申请空间,切记一行都不能少!!(第一次写这个代码在这里调试了很久T_T)
最后说一下,用建树的方法建完二叉树后可用DFS完成三种遍历,用BFS完成按层输出。