title: 斯坦福凸优化课程Video2-2
tags: note
notebook: 6- 英文课程-14-convex optimization
斯坦福凸优化课程Video2-2
超平面和半空间hyperplane and half place
类似于形式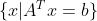 
,就是一种超平面，在这里A和是向量，b是标量，所以x是一个向量，代表了一个平面或者一个超平面（在不同的维度上）。
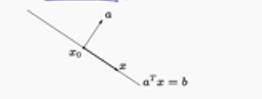
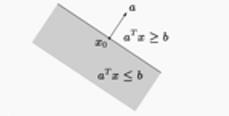
对于半空间，其实就是把上文中平面的方程中的等号边成不等号，所表示的区域就从平面变成了整个空间的一部分，也称为半空间。定义如下：
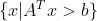
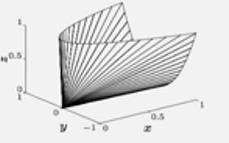
图像如下：
球和椭圆ellipsoids
我们还可以用模的形式对其他的一些图形集合进行描述，比如球
可以用如下的形式描述:
可以看到双竖线描述的是范数，可以理解为距离，这个不等式将x与x0的距离约束到了r以内，就描述了一个球的集合。
还可以用另外一个描述方式，就是圆心和半径的形式，思想式相同的。
当然还可以描述椭球，方程如下：
这个方程式是之前的球的方程的一个边形，不等式左边的是一个二次型，描述了x与xc的二次型的表达。从而描述了一个被压扁的圆，也就是椭圆。
模球和模锥
首先介绍模的概念：模描述的是两个点之间的距离，模有如下三个规则。
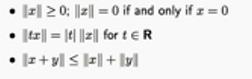
- 第一个是恒大于0
- 第二个是可以提出系数
- 还有就是三角不等式，使用距离的定义都很好理解
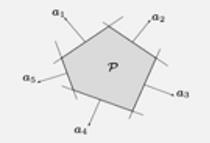
polyhedra 多面体
一系列的线性不等式的解我们称为多面体，线性不等式可以描述为下面的形式：
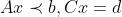
其中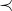
这个符号表示 矩阵的不等关系，这个方程的解再二维条件下得到的解区域为
positive semidefinite cone 正半定锥
下面我们要定义这样几个符号：
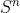是一个n维空间中的集合
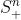是一个集合，集合里的元素满足约束
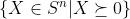，也就是说，对于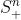中的所有的元素，他们都满足》= 0的约束，我们再下面的例子中也可以看到。
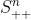这个的概念和上面的 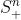差不多，只不过将大于等于变成了严格的大于。
举个例子来说，就是这样，如果我们的方程是这样的：
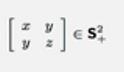
那么得到的解就是，他组成的二次型大于0，画出图像来是这样的。
